Tree (Data Structure)
Traversals
As noted in the Wikipedia article on tree traversal (the notes below make heavy use of this article from conceptual points to pseudocode renderings):
In computer science, tree traversal (also known as tree search and walking the tree) is a form of graph traversal and refers to the process of visiting (e.g., retrieving, updating, or deleting) each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited.
Traversals can apply to any kind of tree (e.g., -ary tree), but binary trees are the ones that come up most often in interviews. Everything below concerns binary trees specifically.
Depth first search (DFS)
The "Tick Trick"
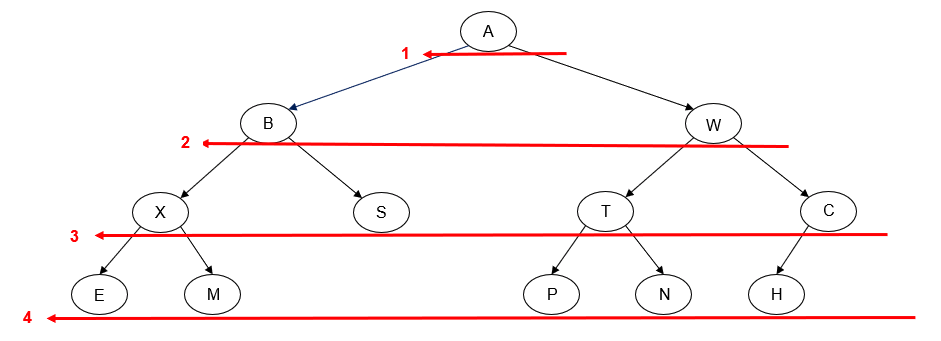
One online resource does a good job of detailing the so-called tick trick, a handy trick for figuring out by hand the order in which a binary tree's nodes will be "visited" for the pre-order, in-order, and post-order traversals:
- Draw an arrow as a path around the nodes of the binary tree diagram, closely following its outline. The direction of the arrow depends on whether you are traversing the tree left-to-right or right-to-left.
- Draw a line or tick mark on one of the sides or the bottom of each node in the tree. Where you draw the mark depends on which traversal you are attempting to perform, as shown in the diagram below:
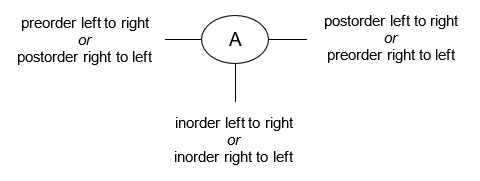
The point at which the path you've drawn around the binary tree intersects the tick mark is the point at which that node will be "visited" during the traversal. Examples for pre-, post-, and in-order traversals are provided below (left-to-right and right-to-left).
It may be tempting to think that right-to-left traversals should effectively be "reversals" of their left-to-right counterparts, but this is not the case for pre- and post-order traversals. It is only the case for in-order traversals.
To see why, recall what the various traversals actually mean. A pre-order traversal means we will visit the current node before traversing either of its subtrees whereas a post-order traversal means we will visit the current node after traversing both of its subtrees. In either case, the root node itself serves as a point of clarification:
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
How could the left-to-right and right-to-left pre-order traversals be reversals of each other if they both start with the same node? Similarly, the post-order traversals cannot be reversals of each other if they both end with the same node. But what about in-order traversals? As can be seen above, the order in which the nodes are visited is reversed when we change the traversal from left-to-right to right-to-left.
It is worth noting that the left-to-right pre-order traversal is effectively the reverse of the right-to-left post-order traversal. Similarly, the left-to-right post-order traversal is effectively the reverse of the right-to-left pre-order traversal.
binarytree Package for PythonLearning about trees can become overly cumbersome if you are specifying all of the nodes yourself. For example, the binary tree in the tip above (and the one we will see throughout the subsections below) may be set up in Python without any package support as follows:
See the setup
class TreeNode:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
n1 = TreeNode('A')
n2 = TreeNode('B')
n3 = TreeNode('W')
n4 = TreeNode('X')
n5 = TreeNode('S')
n6 = TreeNode('T')
n7 = TreeNode('C')
n8 = TreeNode('E')
n9 = TreeNode('M')
n10 = TreeNode('P')
n11 = TreeNode('N')
n12 = TreeNode('H')
n1.left = n2
n1.right = n3
n2.left = n4
n2.right = n5
n4.left = n8
n4.right = n9
n3.left = n6
n3.right = n7
n6.left = n10
n6.right = n11
n7.left = n12
That's not fun. The binarytree package makes things much easier to work with. The same tree can be set up as follows:
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
The code in the sections below will rely on binarytree for the sake of simplicity.
Pre-order
In a pre-order traversal of a binary tree, we "visit" a node and then traverse both of its subtrees. Usually, we traverse the node's left subtree first and then traverse the node's right subtree. Below is an example (using the tick trick) of a left-to-right preorder traversal of a binary tree:
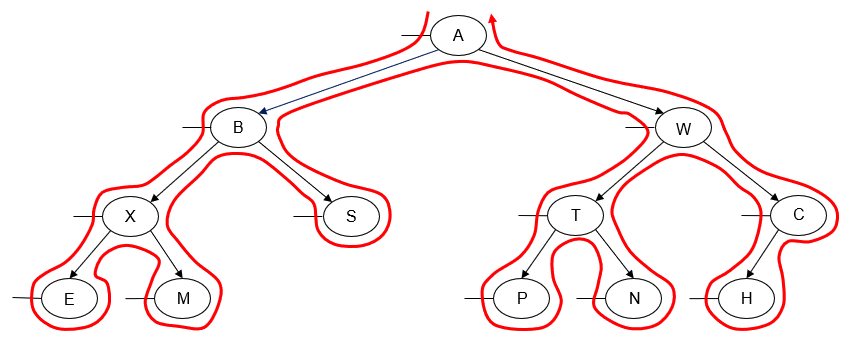
We get the following output by printing the value of each node as we "visit" it:
A B X E M S W T P N C H
Alternatively, we can perform a preorder traversal from right-to-left instead of left-to-right. This is done by traversing the node's right subtree before we traverse its left subtree:
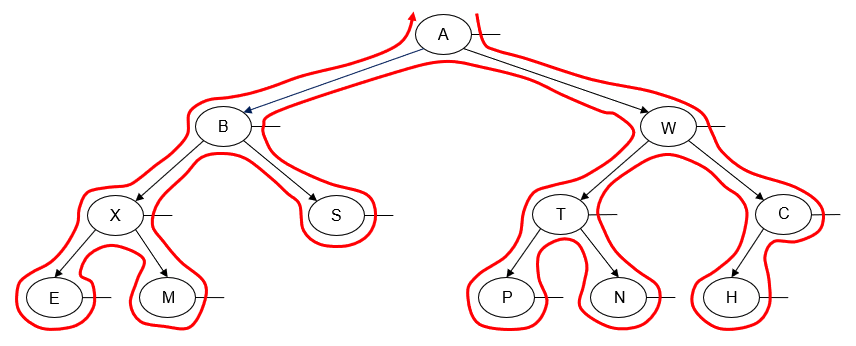
We get the following output by printing the value of each node as we "visit" it:
A W C H T N P B S X M E
Recursive
- Pseudocode
- Python (L->R)
- Python (R->L)
procedure preorder(node)
if node = null
return
visit(node)
preorder(node.left)
preorder(node.right)
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# pre-order recursive left-to-right
def preorder_recursive_LR(node):
if not node:
return
print(node.val)
preorder_recursive_LR(node.left)
preorder_recursive_LR(node.right)
root = bin_tree.levelorder[0]
preorder_recursive_LR(root) # A B X E M S W T P N C H
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# pre-order recursive right-to-left
def preorder_recursive_RL(node):
if not node:
return
print(node.val)
preorder_recursive_RL(node.right)
preorder_recursive_RL(node.left)
root = bin_tree.levelorder[0]
preorder_recursive_RL(root) # A W C H T N P B S X M E
Iterative
- Pseudocode
- Python (L->R)
- Python (R->L)
- Analogy
procedure iterativePreorder(node)
if node = null
return
stack ← empty stack
stack.push(node)
while not stack.isEmpty()
node ← stack.pop()
visit(node)
// right child is pushed first so that left is processed first
if node.right ≠ null
stack.push(node.right)
if node.left ≠ null
stack.push(node.left)
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# pre-order iterative left-to-right
def preorder_iterative_LR(node):
if not node:
return
stack = []
stack.append(node)
while stack:
node = stack.pop()
print(node.val)
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
root = bin_tree.levelorder[0]
preorder_iterative_LR(root) # A B X E M S W T P N C H
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# pre-order iterative right-to-left
def preorder_iterative_RL(node):
if not node:
return
stack = []
stack.append(node)
while stack:
node = stack.pop()
print(node.val)
if node.left:
stack.append(node.left)
if node.right:
stack.append(node.right)
root = bin_tree.levelorder[0]
preorder_iterative_RL(root) # A W C H T N P B S X M E
procedure iterativePreorder(node)
if node = null
return
stack ← empty stack
stack.push(node)
while not stack.isEmpty()
node ← stack.pop()
visit(node)
if node.right ≠ null
stack.push(node.right)
if node.left ≠ null
stack.push(node.left)
Imagine you're a tourist visiting a town rapidly growing in popularity. This town has several attractions, and you want to start by seeing the the main one (root). In an effort to help tourists plan their sightseeing effectively, town leadership organized the attractions in such a way that subsequent attractions are usually recommended once a tourist has finished visiting the current attraction. Any given attraction will recommend either no subsequent attraction (a leaf), a single subsequent attraction, or two subsequent attractions. If two subsequent attractions are recommended, then one will be a primary attraction (left child) and the other a secondary attraction (right child). You want to see as many primary attractions as you can, starting at the main primary attraction, before moving on to secondary attractions, but you want to see them all.
Here's the process you will follow in order to accomplish this:
- Step 1 (start seeing attractions): Begin your sightseeing journey by visiting the town's main attraction (visit the root).
- Step 2 (note the recommendations): If the attraction you just visited recommends another attraction (not a leaf), then make a note of this (push to the stack).
- Step 3 (visit primary attractions first and as encountered): Before exploring the town any further and visiting other attractions, always immediately visit the recommended primary attraction (left child) if it exists.
- Step 4 (note secondary attractions): If the attraction you just visited recommends a secondary attraction (right child), then note this secondary attraction for visiting later (push to the stack), but continue on your current path.
- Step 5 (use your notes to visit more attractions): Once you have finished seeing as many consecutive primary attractions as you can, consult your notes and follow your most recent note about secondary attractions that you've made.
- Step 6 (finish seeing attractions): Continue the pattern of visiting primary attractions as you encounter them and noting down secondary attractions for future visitations until you have explored all attractions in the town.
We can annotate the previously provided Python code to illustrate the steps above (the highlighted line simply serves to show where the logic would be included to process the current node):
def preorder_iterative_LR(node):
# (in case there is no main attraction)
if not node:
return
stack = []
stack.append(node) # Step 1: Start seeing attractions
while stack:
node = stack.pop() # Step 3 or 5: Visit primary attraction (Step 3) OR
# check most recent note for secondary attraction (Step 5)
print(node.val) # Visit the current attraction (process current node)
# Step 4: Note the recommended secondary attraction (if it exists)
if node.right:
stack.append(node.right)
# Step 2: Note the recommended primary attraction (if it exists)
if node.left:
stack.append(node.left)
Note that since stacks are fundamentally LIFO structures (i.e., last in first out) we want to push primary attraction recommendations to the stack after secondary attraction recommendations. This ensures we always get the primary attraction recommendation when we pop from the stack.
This analogy makes it clear the tourist focuses on the primary attractions but neither loses sight of nor forgets the secondary attractions thanks to the notes taken after visiting each attraction (i.e., pushing to the stack).
Post-order
In a postorder traversal of a binary tree, we traverse both subtrees of a node, and then we "visit" the node. Usually we traverse the node's left subtree first and then traverse the node's right subtree:
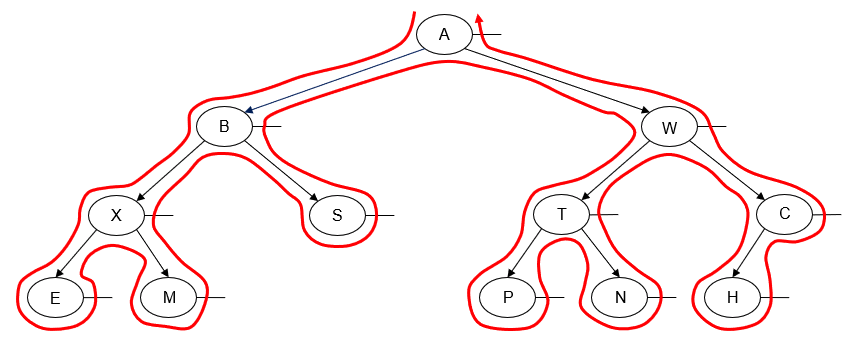
We get the following output by printing the value of each node as we "visit" it:
E M X S B P N T H C W A
Alternatively, we can perform a post-order traversal from right-to-left instead of left-to-right. This is done by traversing the node's right subtree before we traverse its left subtree:
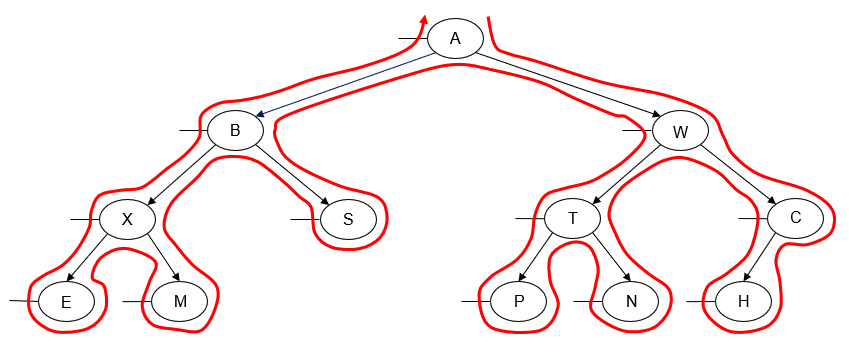
We get the following output by printing the value of each node as we "visit" it:
H C N P T W S M E X B A
Recursive
- Pseudocode
- Python (L->R)
- Python (R->L)
procedure postorder(node)
if node = null
return
postorder(node.left)
postorder(node.right)
visit(node)
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# post-order recursive left-to-right
def postorder_recursive_LR(node):
if not node:
return
postorder_recursive_LR(node.left)
postorder_recursive_LR(node.right)
print(node.val)
root = bin_tree.levelorder[0]
postorder_recursive_LR(root) # E M X S B P N T H C W A
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# post-order recursive right-to-left
def postorder_recursive_RL(node):
if not node:
return
postorder_recursive_RL(node.right)
postorder_recursive_RL(node.left)
print(node.val)
root = bin_tree.levelorder[0]
postorder_recursive_RL(root) # H C N P T W S M E X B A
Iterative
- Pseudocode
- Python (L->R)
- Python (R->L)
- Analogy
procedure iterativePostorder(node)
stack ← empty stack
lastNodeVisited ← null
while not stack.isEmpty() or node ≠ null
if node ≠ null
stack.push(node)
node ← node.left
else
peekNode ← stack.peek()
// if right child exists and traversing node
// from left child, then move right
if peekNode.right ≠ null and lastNodeVisited ≠ peekNode.right
node ← peekNode.right
else
visit(peekNode)
lastNodeVisited ← stack.pop()
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# post-order iterative left-to-right
def postorder_iterative_LR(node):
stack = []
last_node_visited = None
while stack or node:
if node:
stack.append(node)
node = node.left
else:
peek_node = stack[-1]
if peek_node.right and (last_node_visited is not peek_node.right):
node = peek_node.right
else:
print(peek_node.val)
last_node_visited = stack.pop()
root = bin_tree.levelorder[0]
postorder_iterative_LR(root) # E M X S B P N T H C W A
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# post-order iterative right-to-left
def postorder_iterative_RL(node):
stack = []
last_node_visited = None
while stack or node:
if node:
stack.append(node)
node = node.right
else:
peek_node = stack[-1]
if peek_node.left and (last_node_visited is not peek_node.left):
node = peek_node.left
else:
print(peek_node.val)
last_node_visited = stack.pop()
root = bin_tree.levelorder[0]
postorder_iterative_RL(root) # H C N P T W S M E X B A
procedure iterativePostorder(node)
stack ← empty stack
lastNodeVisited ← null
while not stack.isEmpty() or node ≠ null
if node ≠ null
stack.push(node)
node ← node.left
else
peekNode ← stack.peek()
if peekNode.right ≠ null and lastNodeVisited ≠ peekNode.right
node ← peekNode.right
else
visit(peekNode)
lastNodeVisited ← stack.pop()
def postorder_iterative_LR(node):
stack = []
last_node_visited = None
while stack or node:
if node:
stack.append(node)
node = node.left
else:
peek_node = stack[-1]
if peek_node.right and (last_node_visited is not peek_node.right):
node = peek_node.right
else:
print(peek_node.val)
last_node_visited = stack.pop()
Imagine you're exploring a series of underground caves, where the caves have multiple tunnels (paths) and chambers (nodes) connected in a complex network. Your ultimate goal is to mark each chamber as having been "Explored", but you can only mark a chamber as having been "Explored" if you have explored all the deeper chambers (children) accessible from it. To accomplish this task, you have been given a piece of chalk for marking chambers and a map to record where you have been. Every time you enter a new chamber, you mark it on your map (push it to the stack), but you hold off on marking the chamber as "Explored" until you've visited every chamber accessible from it.
Here's the process you will follow in order to accomplish this:
- Step 1 (begin the exploration): Enter the first chamber (root).
- Step 2 (check for a left tunnel): Check for a left tunnel. If there is a left tunnel, then mark this chamber on your map (push to the stack) and venture down the left tunnel.
- Step 3 (exhaust all left tunnels): Continue to the deepest chamber you can reach by always taking left tunnels.
- Step 4 (check for a right tunnel): Check for a right tunnel once you find yourself in a chamber with no left tunnel or where all left chambers have been marked as "Explored".
- Step 5 (venture down a right tunnel): If there's an unexplored right tunnel, mark your current chamber on the map (it's still on the stack) and venture down the right tunnel.
- Step 6 (mark a chamber as "Explored"): If there's no right tunnel or if it's already been explored, then this chamber is now the deepest unexplored one, so you can mark it as "Explored" (visit the node by printing its value). Then cross it off your map (pop it from the stack) and backtrack.
- Step 7 (continue the process): Continue the process described above. Every time you backtrack to a chamber, check its right tunnel. If it's unexplored, then venture in. If it's explored or non-existent, then mark the chamber as "Explored" and backtrack further.
- Step 8 (return to the entrance): Keep doing everything above until you've marked every chamber as "Explored" and have returned to the cave entrance.
Essentially, you will be venturing down as deep as you can, marking chambers as "Explored" on your way out, ensuring the deeper chambers are always marked as "Explored" before the shallower ones from which they are accessible.
We can annotate the previously provided Python code to illustrate the steps above (the highlighted line simply serves to show where the logic would be included to process the current node):
def postorder_iterative_LR(node):
stack = []
last_node_visited = None
# Step 1: Enter the cave system. As long as there's a chamber to explore
# or a path in the stack to backtrack to, continue.
while stack or node:
# Step 2: If you're in a new chamber, then mark the path you took
# to get there (push it onto a stack).
if node:
stack.append(node)
# Step 3: Always check the left tunnel of the current chamber first.
# If there is one, you go down it.
node = node.left
else:
# Step 4: If there's no left tunnel or after coming back
# from a left tunnel, you're ready to check the right tunnel.
peek_node = stack[-1]
# Step 5: Before checking the right tunnel,
# make sure you haven't just explored it.
# If not, you go down the right tunnel.
if peek_node.right and (last_node_visited is not peek_node.right):
node = peek_node.right
else:
# Step 6: If no tunnels remain to explore from current chamber,
# or if you've just explored the right tunnel, then
# it's time to mark the current chamber as "Explored"
print(peek_node.val)
# Step 7: After marking the chamber as "Explored", you backtrack.
# The last path you took (from the stack) will help you go back.
last_node_visited = stack.pop()
# Step 8: When you've explored every chamber and every tunnel,
# and there's no path left in your stack,
# you exit the cave system.
It's worth specifically noting what the following if block accomplishes in the code above:
if peek_node.right and (last_node_visited is not peek_node.right):
node = peek_node.right
peek_node.right: This checks whether or nor the current chamber (represented bypeek_node) has a right tunnel and answers the question, "Is there a right tunnel leading out of this chamber?"last_node_visited is not peek_node.right: This checks if the right tunnel/chamber (peek_node.right) was the last one you explored. If it was, then you've already visited it and don't need to venture down there again. It answers the question, "Did I just come from that right tunnel, or have I not explored it yet?"node = peek_node.right: If the current chamber has an unexplored right tunnel, then prepare to venture into it. This assignment is effectively saying, "I haven't explored the right tunnel of this chamber yet. Let's go down there next."
Essentially, the if block above ensures you explore a chamber's right tunnel if you haven't already — if you've just come back from exploring the right tunnel (i.e., last_node_visited is peek_node.right is True), then you know it's time to mark the current chamber as "Explored" and backtrack.
The procedure outlined above is rather sophisticated and complex in its logic — it is probably easiest to understand if we actually work through a concrete example such as the one provided below (writing out the process may seem tedious, and it is, but it's worth following the first time around to provide some sort of intuition for things).
Concrete example using a familiar binary tree
We have used the following binary tree in a number of previous examples:
__A______
/ \
__B __W__
/ \ / \
X S T C
/ \ / \ /
E M P N H
For the sake of our example, suppose each node represents a chamber of a cave. Then the entrance to the cave system is marked by the root node, A. Let's start exploring the cave and try to mark all chambers as "Explored" by using our previously described process, where the order in which the chambers should be marked as "Explored" should be E M X S B P N T H C W A in order to hold true to a post-order traversal (each bullet point below represents an iteration of the while loop where each bullet point ends with the current state of explored chambers):
-
We start by entering the cave system, leading us into chamber
A. We push this on to the stack:| A |
+---+We attempt to go to chamber
A's left tunnel if there is one. There is. We update the current node to point to chamberB.Explored chambers:
[] -
We push
Bon to the stack:| B |
| A |
+---+We attempt to go to chamber
B's left tunnel if there is one. There is. We update the current node to point to chamberX.Explored chambers:
[] -
We push
Xon to the stack:| X |
| B |
| A |
+---+We attempt to go to chamber
X's left tunnel if there is one. There is. We update the current node to point to chamberE.Explored chambers:
[] -
We push
Eon to the stack:| E |
| X |
| B |
| A |
+---+We attempt to go to chamber
E's left tunnel if there is one. There is not. We update the current node to point toNone.Explored chambers:
[] -
Since
nodecurrently points toNone, we do not need to check for a left tunnel. Instead, we need to check for a right tunnel.peek_node = stack[-1]meanspeek_nodepoints to nodeEsinceEis on top of the stack.peek_node.righthas no meaningful value since chamberEhas no right tunnel; hence, no tunnels remain to explore from our current chamber. We can mark chamberEas "Explored". To keep track of which chamber we last visited and to update our stack of chambers we still need to explore, we letlast_node_visited = stack.pop(), meaninglast_node_visitednow points to nodeE, and our updated stack looks as follows:| X |
| B |
| A |
+---+Explored chambers:
[ E ] -
Since
nodestill points toNone, we do not need to check for a left tunnel. Instead, we need to check for a right tunnel.Simplify Matters by Understanding the Possible Outcomes for Each IterationIt is easy to get lost in some of the fancy referential footwork used in the iterative post-order traversal. But note the only possible outcomes for each iteration of the
whileloop:-
(left tunnel exists): enter chamber of left tunnel and keep going left until you can go no further
-
(no left tunnel; no right tunnel): mark the chamber as explored (print the node's value), note the chamber as being the last one explored, and remove the chamber from the stack of chambers waiting to be explored
-
(no left tunnel; right tunnel exists, not yet explored): enter chamber of right tunnel and try to explore its left tunnels if it has any
-
(no left tunnel; right tunnel exists, already explored): this is effectively the same as neither having a left tunnel nor a right tunnel — follow the guidelines above concerning that scenario
Essentially, you're going left or right if you can; otherwise, you're marking the chamber as having been explored (printing its value), noting that you just explored it so you don't explore it again and updating the stack of chambers that need exploring (popping from the stack the chamber you just visited and referring to it as
last_node_visited).Since
Xnow sits at the top of the stack,peek_node = stack[-1]meanspeek_nodepoints to chamberX. This timepeek_node.rightdoes have a meaningful value since there is a right tunnel from chamberXthat leads into chamberM. Before we visit chamberM, however, we need to ask ourselves, "Have we visited chamberMyet?" Sincelast_node_visitedpoints to chamberEand not chamberM, we can safely assume we have not yet visited chamberM. As such, we should prepared to visit chamberM. Updatenodeto point to chamberM.Explored chambers:
[ E ] -
-
We push
Mon to the stack:| M |
| X |
| B |
| A |
+---+We attempt to go to chamber
M's left tunnel if there is one. There is not. We update the current node to point toNone.Explored chambers:
[ E ] -
peek_node = stack[-1]now points to chamberM. There's no right tunnel from chamberM. Mark chamberMas having been explored, and pop it from the stack of chambers we still need to visit (make sure to keep a reference to this most recently explored chamber as well):| X |
| B |
| A |
+---+Explored chambers:
[ E M ] -
Since
nodestill points toNone, we look at chamberpeek_node = stack[-1], which points again to chamberX. Note thatpeek_node.rightgives a meaningful value, namely chamberM. But we just visited chamberMand marked it as explored. Visiting chamberMagain would not make any sense. Fortunately, we noted which chamber we last visited withlast_node_visited. This variable points to chamberM.Hence, the second part of the
andportion ofpeek_node.right and (last_node_visited is not peek_node.right)is false, meaning we do not explore the right tunnel (i.e., chamber
M). This means we can now safely mark chamberXas having been explored (since all chambers beneath it on the left and right have now been explored) as well as update our stack and our "most recently visited chamber" reference:| B |
| A |
+---+Explored chambers:
[ E M X ] -
The pattern may start to emerge more clearly now.
nodestill points toNone.peek_node = stack[-1]meanspeek_nodenow points to chamberB. We see thatpeek_node.righthas a meaningful value, namely chamberS. Furthermore,last_node_visitedpoints to chamberX, not chamberS. Hence, we should explore the right tunnel from chamberBthat begins with chamberS.Explored chambers:
[ E M X ] -
nodenow points to chamberS. Push it to the stack:| S |
| B |
| A |
+---+We attempt to go to chamber
S's left tunnel if there is one. There is not. We update the current node to point toNone.Explored chambers:
[ E M X ] -
nodenow points toNone. Andpeek_node = stack[-1]points to chamberS. Andpeek_node.rightdoes not give a meaningful value, meaning chamberShas no right tunnel. Mark chamberSas explored and pop it from the stack:| B |
| A |
+---+Update our reference for the most recently explored chamber.
Explored chambers:
[ E M X S ] -
nodepoints toNone.peek_node = stack[-1]points to chamberBagain.peek_node.rightpoints to chamberS, butlast_node_visitedalso points to chamberS. Hence, mark chamberBas explored and pop it from the stack:| A |
+---+Update our reference for the most recently explored chamber.
Explored chambers:
[ E M X S B ] -
nodepoints toNone.peek_node = stack[-1]points to chamberA.peek_node.rightpoints to chamberW. Sincelast_node_visitedpoints to chamberBand not chamberW, this means we should prepare to visit the right tunnel from chamberAthat begins with chamberW. Updatenodeto point to chamberW.Explored chambers:
[ E M X S B ] -
nodepoints to chamberW. Push it to the stack:| W |
| A |
+---+We attempt to go to chamber
W's left tunnel if there is one. There is. We update the current node to point to chamberT.Explored chambers:
[ E M X S B ] -
nodepoints to chamberT. Push it to the stack:| T |
| W |
| A |
+---+We attempt to go to chamber
T's left tunnel if there is one. There is. We update the current node to point to chamberP.Explored chambers:
[ E M X S B ] -
nodepoints to chamberP. Push it to the stack:| P |
| T |
| W |
| A |
+---+We attempt to go to chamber
P's left tunnel if there is one. There is not. We update the current node to point toNone.Explored chambers:
[ E M X S B ] -
nodepoints toNone. Andpeek_node = stack[-1]points to chamberP. Sincepeek_node.rightdoes not have a meaningful value (i.e., chamberPhas no right tunnel), we may mark chamberPas explored and pop it from the stack:| T |
| W |
| A |
+---+Update our reference for the most recently explored chamber.
Explored chambers:
[ E M X S B P ] -
nodepoints toNone. Andpeek_node = stack[-1]points to chamberT. We look for a right tunnel and see thatpeek_node.rightreveals chamberN. Sincelast_node_visitedpoints to chamberPand not chamberN, we prepare to explore chamberN. Updatenodeto point to chamberN.Explored chambers:
[ E M X S B P ] -
nodepoints to chamberN. Push it to the stack:| N |
| T |
| W |
| A |
+---+We attempt to go to chamber
N's left tunnel if there is one. There is not. We update the current node to point toNone.Explored chambers:
[ E M X S B P ] -
nodepoints toNone. Andpeek_node = stack[-1]points to chamberN. Sincepeek_node.rightdoes not provide a meaningful value (i.e., chamberNhas no right tunnel), we may mark chamberNas explored and pop it from the stack:| T |
| W |
| A |
+---+Update our reference for the most recently explored chamber.
Explored chambers:
[ E M X S B P N ] -
nodepoints toNone. Andpeek_node = stack[-1]points to chamberTagain. Andpeek_node.rightpoints to chamberN. Butlast_node_visitedalso points to chamberN, indicating we should not explore chamberN. Instead, we should mark chamberTas explored and pop it from the stack:| W |
| A |
+---+Update our reference for the most recently explored chamber.
Explored chambers:
[ E M X S B P N T ] -
nodepoints toNone. Andpeek_node = stack[-1]points to chamberW. Andpeek_node.rightpoints to chamberC. Sincelast_node_visitedpoints to chamberTand not chamberC, we should prepare to visit chamberC. Updatenodeto point to chamberC.Explored chambers:
[ E M X S B P N T ] -
nodepoints to chamberC. Push it to the stack:| C |
| W |
| A |
+---+We attempt to go to chamber
C's left tunnel if there is one. There is. We update the current node to point to chamberH.Explored chambers:
[ E M X S B P N T ] -
nodepoints to chamberH. Push it to the stack:| H |
| C |
| W |
| A |
+---+We attempt to go to chamber
H's left tunnel if there is one. There is not. We update the current node to point toNone.Explored chambers:
[ E M X S B P N T ] -
nodepoints toNone. Andpeek_node = stack[-1]points to chamberH. Sincepeek_node.rightdoes not provide a meaningful value, we may mark chamberHas being explored and pop it from the stack:| C |
| W |
| A |
+---+Update our reference for the most recently explored chamber.
Explored chambers:
[ E M X S B P N T H ] -
nodepoints toNone. Andpeek_node = stack[-1]points to chamberC. Sincepeek_node.rightdoes not provide a meaningful value, we may mark chamberCas explored and pop it from the stack:| W |
| A |
+---+Update our reference for the most recently explored chamber.
Explored chambers:
[ E M X S B P N T H C ] -
nodepoints toNone. Andpeek_node = stack[-1]points to chamberW. Even thoughpeek_node.rightpoints to chamberC, we see thatlast_node_visitedalso points to chamberC, meaning we should not visit chamberC. Mark chamberWas explored and pop it from the stack:| A |
+---+Update our reference for the most recently explored chamber.
Explored chambers:
[ E M X S B P N T H C W ] -
nodepoints toNone. Andpeek_node = stack[-1]points to chamberA. Even thoughpeek_node.rightpoints to chamberW, we see thatlast_node_visitedalso points to chamberW, meaning we should not visit chamberW. Mark chamberAas explored and pop it from the stack:[]Update our reference for the most recently explored chamber.
Explored chambers:
[ E M X S B P N T H C W A ]
The while loop does not fire now since node still points to None and stack is now empty. The iterative post-order traversal is now complete, and we see we have visited the chambers in the expected order:
E M X S B P N T H C W A
In sum, iterative post-order traversals can be rather complicated, but can also be elegant nonetheless.
In-order
In an in-order traversal of a binary tree, we traverse one subtree of a node, then "visit" the node, and then we traverse its other subtree. Usually, we traverse the node's left subtree first and then traverse the node's right subtree:
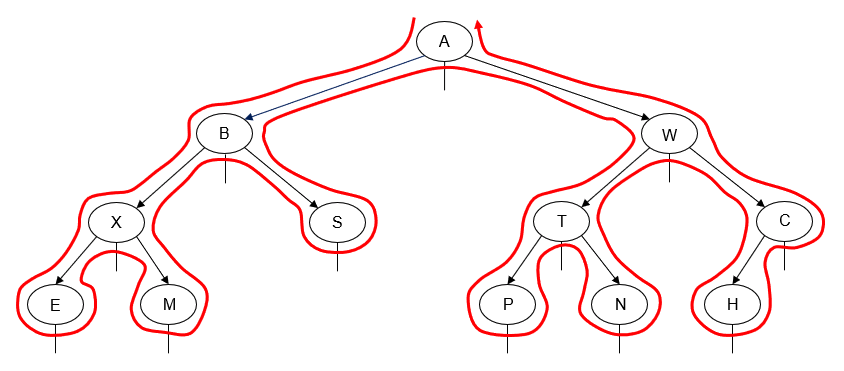
We get the following output by printing the value of each node as we "visit" it:
E X M B S A P T N W H C
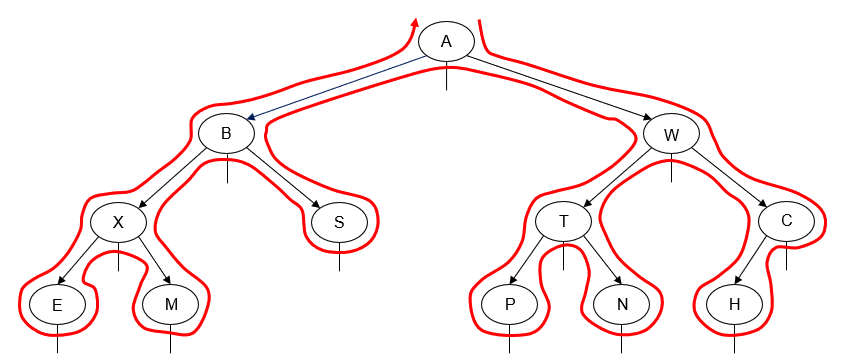
Alternatively, we can perform an in-order traversal from right-to-left instead of left-to-right. This is done by traversing the node's right subtree before we traverse its left subtree:
C H W N T P A S B M X E
Recursive
- Pseudocode
- Python (L->R)
- Python (R->L)
procedure inorder(node)
if node = null
return
inorder(node.left)
visit(node)
inorder(node.right)
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# in-order recursive left-to-right
def inorder_recursive_LR(node):
if not node:
return
inorder_recursive_LR(node.left)
print(node.val)
inorder_recursive_LR(node.right)
root = bin_tree.levelorder[0]
inorder_recursive_LR(root) # E X M B S A P T N W H C
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# in-order recursive right-to-left
def inorder_recursive_RL(node):
if not node:
return
inorder_recursive_RL(node.right)
print(node.val)
inorder_recursive_RL(node.left)
root = bin_tree.levelorder[0]
inorder_recursive_RL(root) # C H W N T P A S B M X E
Iterative
- Pseudocode
- Python (L->R)
- Python (R->L)
- Analogy
procedure iterativeInorder(node)
stack ← empty stack
while not stack.isEmpty() or node ≠ null
if node ≠ null
stack.push(node)
node ← node.left
else
node ← stack.pop()
visit(node)
node ← node.right
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# in-order iterative left-to-right
def inorder_iterative_LR(node):
stack = []
while stack or node:
if node:
stack.append(node)
node = node.left
else:
node = stack.pop()
print(node.val)
node = node.right
root = bin_tree.levelorder[0]
inorder_iterative_LR(root) # E X M B S A P T N W H C
__A______ | Pre-order (L -> R): A B X E M S W T P N C H
/ \ | Pre-order (R -> L): A W C H T N P B S X M E
__B __W__ | Post-order (L -> R): E M X S B P N T H C W A
/ \ / \ | Post-order (R -> L): H C N P T W S M E X B A
X S T C | In-order (L -> R): E X M B S A P T N W H C
/ \ / \ / | In-order (R -> L): C H W N T P A S B M X E
E M P N H |
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# in-order iterative right-to-left
def inorder_iterative_RL(node):
stack = []
while stack or node:
if node:
stack.append(node)
node = node.right
else:
node = stack.pop()
print(node.val)
node = node.left
root = bin_tree.levelorder[0]
inorder_iterative_RL(root) # C H W N T P A S B M X E
procedure iterativeInorder(node)
stack ← empty stack
while not stack.isEmpty() or node ≠ null
if node ≠ null
stack.push(node)
node ← node.left
else
node ← stack.pop()
visit(node)
node ← node.right
Imagine you're reading a book series. Specifically, let's suppose you're reading the Jack Ryan series of novels by Tom Clancy. You've heard a lot about this series and know several books have film adaptations. You'd like to check it out. The first book you check out, Debt of Honor, seems to probably end with Jack Ryan becoming the President of the United States. That can't be right. Surely there's a lot more to Jack Ryan's story that led up to that point. You'd really like to read the whole book series in order, specifically by chronological order of events as opposed to publication date.
Jack Ryan novels by chronological order of events
The excerpt below is from ChatGPT (Aug 19, 2023).
Tom Clancy's Jack Ryan series, with its complex web of interconnected characters and plots, can be arranged according to the internal chronological order of events rather than their publication dates. This order provides a coherent understanding of Jack Ryan's life, from a young Marine to President of the United States, as well as the lives of other recurring characters.
Here's the chronological ordering of the Jack Ryan series based on character development and the events in the series:
-
Without Remorse (1993) - This novel serves as a prequel to the series, focusing on the backstory of John Kelly (who later becomes John Clark), a recurring character in many of the Jack Ryan books.
-
Red Rabbit (2002) - Set in the early 1980s, this book details a younger Jack Ryan's time with the CIA and a plot to assassinate Pope John Paul II.
-
The Hunt for Red October (1984) - This is the first novel published in the series, introducing Jack Ryan as an analyst for the CIA as he gets involved in the defection of a Soviet submarine captain.
-
The Cardinal of the Kremlin (1988) - Jack Ryan becomes involved in a high-stakes espionage game as the Americans and the Soviets vie for technological dominance.
-
Clear and Present Danger (1989) - Jack Ryan is a National Security Advisor here, and the story revolves around U.S. efforts against Colombian drug cartels.
-
The Sum of All Fears (1991) - Jack Ryan, now Deputy Director of Intelligence for the CIA, must prevent a nuclear conflict between the U.S. and Russia.
-
Debt of Honor (1994) - The focus shifts to the Pacific, with an escalating conflict between the U.S. and Japan. By the end of the novel, Jack Ryan is thrust into the role of President of the United States.
-
Executive Orders (1996) - Continuing directly from where "Debt of Honor" left off, President Ryan faces both internal and external challenges, including rebuilding the U.S. government and dealing with an Ebola-like epidemic.
-
The Bear and the Dragon (2000) - President Jack Ryan oversees a complex geopolitical situation involving China, Russia, and the prospect of World War III.
-
Red Storm Rising (1986) - While not strictly a Jack Ryan novel (he doesn't appear in it), this book is set in the same universe and involves a war between NATO and Warsaw Pact forces.
-
The Teeth of the Tiger (2003), Dead or Alive (2010), Locked On (2011), Threat Vector (2012), and Command Authority (2013) - These novels follow the next generation, including Jack Ryan Jr., as they face modern threats in a post-9/11 world. Jack Ryan Sr. still plays a role, but the torch is being passed to the younger characters.
It's worth noting that Tom Clancy's name has been attached to books written by other authors after his death in 2013. If you're interested in the books in this universe that continue the story or explore other side characters, there's an extended series to dive into, but the above list covers the main Jack Ryan saga as written by Clancy himself.
As fate would have it, the book you just started with (the root) has both prequel and sequel recommendations. Some books you encounter may have no recommendations (leaf nodes), but you want to prioritize tracing back through each preqel recommendation (left child) so you can start at the beginning of the series, but you also need to try to read the sequel (right child) for each book, as recommended.
Here's the process you will follow in order to accomplish this:
- Step 1 (start with the first book in the series): Follow all prequel recommendations (left children) from your starting point (root) until they have all been exhausted (you hit a leaf node), noting each book along the way that recommends a prequel (push it to the stack).
- Step 2 (follow recommendations): If your current book has a prequel recommendation (left child), then set it aside to be read later (push it to the stack).
- Step 3 (keep following recommendations): If the new book also has a prequel recommendation, then repeat the process: set the new book aside to read later, and pick up the recommended prequel. Continue this process until you reach a book with no prequel recommendation.
- Step 4 (read the book): Once there is no prequel left to read, read the book (visit the node).
- Step 5 (move to sequel recommendation or return to books previously set aside): Always attempt to move on to a sequel recommendation (right child) after having read a book (once the node has been visited). If there is no such sequel recommendation, then move back to the most recent book you've set aside but have not yet read (pop from the stack). Continue.
- Step 6 (repeat until all books are read): Repeat the steps above until you have finished all books in the series.
We can annotate the previously provided Python code to illustrate the steps above (the highlighted line simply serves to show where the logic would be included to process the current node):
def inorder_iterative_LR(node):
stack = []
# there is still a book to be read
while stack or node:
# Steps 1-3: Follow prequel recommendations
if node:
stack.append(node) # Step 2: Set aside the current book
node = node.left
else:
# Step 4: Read the current book
node = stack.pop()
print(node.val)
# Step 5: Move to sequel recommendation
node = node.right
Note that this analogy involves a highly contrived example. If we followed the numbering of the Jack Ryan books in chronological ordering after starting with book 7 as the root, then the most sensible binary tree would look rather ridiculous:
7
/ \
6 8
/ \
5 9
/ \
4 10
/ \
3 11
/
2
/
1
But technically any other ordering would work so long as 7 was the root and the in-order traversal led to books 1 through 11 being listed in sequence. One such example:
__7__
/ \
__5 9
/ \ / \
3 6 8 10
/ \ \
2 4 11
/
1
Breadth first search (BFS)
Level order traversal
In a level order traversal of a binary tree, we traverse all of the tree nodes on level 0, then all of the nodes on level 1, etc. The "tick trick" does not work for this traversal, but there's no real need for it, since the order the nodes will be traversed is easy to determine by hand.
Below is an example of a left-to-right level-order traversal of a binary tree:
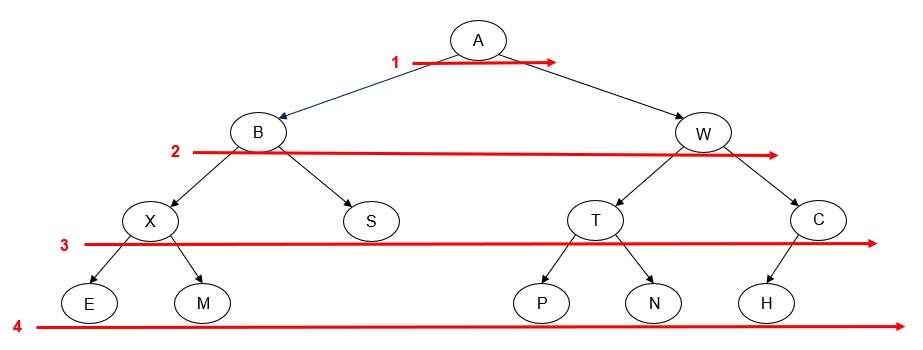
We get the following output by printing the value of each node as we "visit" it:
A B W X S T C E M P N H
Alternatively, we can perform a level order traversal from right-to-left instead of left-to-right:
We get the following output by printing the value of each node as we "visit" it:
A W B C T S X H N P M E
- Pseudocode
- Python (L->R)
- Python (R->L)
- Recursive
- Analogy
procedure levelorder(node)
queue ← empty queue
queue.enqueue(node)
while not queue.isEmpty()
node ← queue.dequeue()
visit(node)
if node.left ≠ null
queue.enqueue(node.left)
if node.right ≠ null
queue.enqueue(node.right)
The pseudocode above (from Wikipedia) is the standard BFS implementation for a binary tree traversal, where we only care about visiting all nodes, level by level, left to right. But it's fairly common to encounter algorithm problems that demand you do something (i.e., perform some logic) on a level by level basis; that is, you effectively need to isolate the nodes by level. The pseudocode above does not do this, but we can easily fix this ourselves:
procedure levelorder(node)
queue ← empty queue
queue.enqueue(node)
while not queue.isEmpty()
// retrieve number of nodes on current level
numNodesThisLevel ← queue.length
// perform logic for current level
for each node in level do
node ← queue.dequeue()
// perform logic on current node
visit(node)
// enqueue nodes on next level (left to right)
if node.left ≠ null
queue.enqueue(node.left)
if node.right ≠ null
queue.enqueue(node.right)
The Python code snippets in the other tabs reflect this approach since it is the most likely approach needed in the context of solving interview problems.
from collections import deque
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# level-order left-to-right
def levelorder_LR(node):
queue = deque()
queue.append(node)
while queue:
num_nodes_this_level = len(queue)
for _ in range(num_nodes_this_level):
node = queue.popleft()
print(node.val)
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
root = bin_tree.levelorder[0]
levelorder_LR(root) # A B W X S T C E M P N H
from collections import deque
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
# level-order right-to-left
def levelorder_RL(node):
queue = deque()
queue.append(node)
while queue:
num_nodes_this_level = len(queue)
for _ in range(num_nodes_this_level):
node = queue.popleft()
print(node.val)
if node.right:
queue.append(node.right)
if node.left:
queue.append(node.left)
root = bin_tree.levelorder[0]
levelorder_RL(root) # A W B C T S X H N P M E
As this Stack Overflow post explores, breadth-first search can be done recursively, but this does not mean it should be done recursively. It's quite a bit more complex than the iterative solution with basically no added benefit (instead of using a queue to explicitly do things efficiently we would now just be implicitly using the call stack).
That said, here's a possible recursive approach to a level-order traversal for our binary tree:
from binarytree import build2
bin_tree = build2(['A', 'B', 'W', 'X', 'S', 'T', 'C', 'E', 'M', None, None, 'P', 'N', 'H'])
root = bin_tree.levelorder[0]
def level_order(root):
h = height(root)
for i in range(1, h + 1):
print_level(root, i)
def print_level(node, level):
if not node:
return
if level == 1:
print(node.val)
elif level > 1:
print_level(node.left, level - 1)
print_level(node.right, level - 1)
def height(node):
if not node:
return 0
l_height = height(node.left)
r_height = height(node.right)
return max(l_height, r_height) + 1
level_order(root) # A B W X S T C E M P N H
tbd