Lists, stacks, and queues (with attitude)
This post aims to introduce list, stack, and queue data structures with discussions about implementation and analysis.
The notes below come from the Algorithms with Attitude YouTube channel, specifically the Lists, Stacks, and Queues playlist comprised of the following videos: Lists, Iterators, and Abstract Data Types, Linked Lists, Dynamic Arrays, aka ArrayLists, Advanced Dynamic Arrays, Linked Lists and Dynamic Arrays: Misuse and Abuse, Stacks, Queues, and Double Ended Queues (Deques).
There are several sections in this post, accessible in the table of contents on the right, but most of the sections have been listed below for ease of reference and navigation.
Lists, iterators, and abstract data types (ADTs)
Lists
Here's a seemingly simplistic or reductive definition of a list:
List: Some stuff. In some order.
But there's actually something important hidden in this definition, which is that the list is an abstract data type (ADT). What's that?
Abstract Data Type (ADT)
This is the formal name of the "stuff" mentioned in the list definition. We can have a list of integers, strings, records, or whatever else we might like. Although a few details might change, the basic logic of how the list works stays the same no matter what it is that's actually in the list; that is, the list structures and methods are (almost) independent of what is stored in the list.
What types of things might change? Maybe for integers we just want to store the integers, but for larger objects we might want to store object references instead of the objects themselves. Some of this might be language-specific, but it doesn't make too much of a difference for the underlying algorithmic logic.
Iterator
What actually is an iterator? It's basically a list bookmark. If we're making a list data structure for somebody else to use, then we should give that user a way to access the items in our list, one at a time. It's probably fine for them to ask for the first item in the list, but it is less natural for them to ask for the second or third. Instead of having the user track where they are, which might cause some efficiency issues, it makes more sense to allow the user to just ask for the next item, and the next, and to give them items that way. Our iterator might also allow other operations, but its code is written as a partner of the list code, which keeps constrol of the list and its internal implementation away from the outsider user (i.e., "bookmark" or iterator allows the outsider to walk through our list while not breaking the abstraction barrier).
Summary (list, ADT, iterator)
Let's summarize what we have so far:
- List: Some stuff. In some order. Abstract Data Type (ADT)
- Abstract Data Type: Technical name for "stuff". The list structures and methods are (almost) independent of what it is stored in the list (for instance, integers, strings, records, topics).
- Iterators: Bookmark for an outsider to walk through our list while not breaking the abstraction barrier.
List operations
So what functionality do we expect from a list?
- Create
- Retrieve
- Insert (by location?)
- Delete (by key or location?)
- Size
There obviously needs to be some way to create the list, and after that, we need some way to retrieve items. Assuming the list can change, we can add to the list, remove from the list, and know its size.
Iterator operations
To traverse the list and iterate over its items, we want an iterator that, at the very least, can give us the next item in the list, starting at the beginning. Maybe we can do some other stuff too, but we don't want to get overly precise here because a list is very abstract.
Standard techniques for building a list
Depending on which implementation strategy we use to build our list, we get different natural functionality. The two most standard techniques for building a list are to use what is called a linked list or to use an array-based list. In Java, these are respectively called LinkedList and ArrayList, but we can use the same strategy in lots of languages.
Linked lists
Definition by example
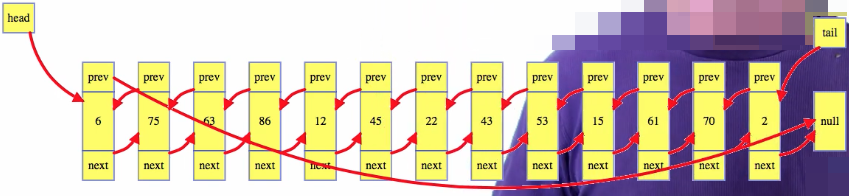
A linked list is a chain of nodes, where each node keeps track of some data as well as a reference to the next node in the list. Usually, we can just imagine that the information stored for each node is just some integer:

But lists are Abstract Data Types, so a node can store anything we want. Now, even though we tend to draw the list nicely, like above, the nodes are really just "out there" in our computer's memory. More realistically, it's much less organized:
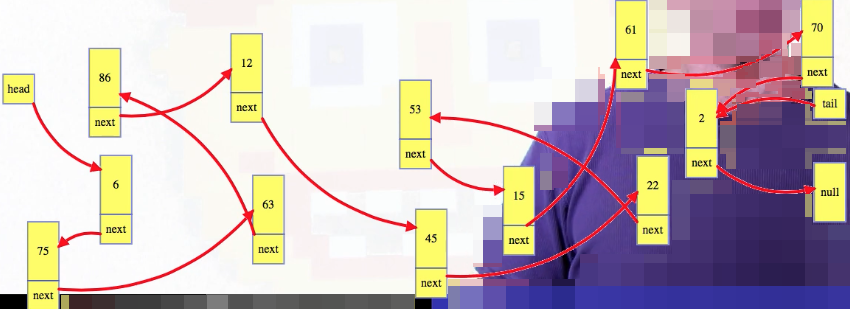
The linked list data structure just needs to keep track of the first (i.e., "head") node and maybe the last (i.e., "tail") node. Those two locations are the only easy ones to get to.
Other node references are only stored in one or two adjacent nodes. To get to nodes in the middle of the list, we follow the chain of nodes from the head. Now, above is the traditional singly linked list, from back in the stone ages, when computers were made out of stone. Now that memory isn't so limited, we usually go with a doubly linked list, where each node also keeps track of the previous node:
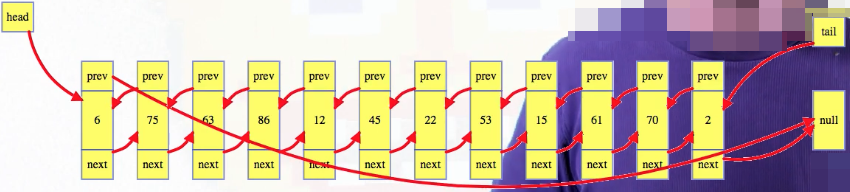
They have more functionality, and can actually be coded more cleanly, so we will focus on them.
Insert
We start by inserting into an already built list at an arbitrary spot. Linked lists do not support indexing efficiently, but suppose that the spirit of Alan Turing hands us a reference to an arbitrary node in the middle of the list, and we want to insert a new node after that one. Below, suppose we want to insert a 43 node right after the 22 node, given a reference to the node with 22:
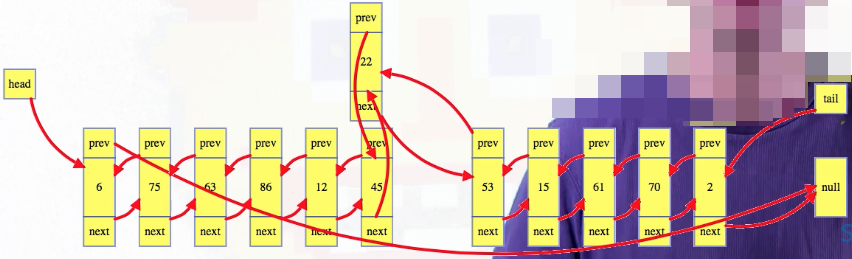
For every insertion, we start by creating a new node, with the new data, 43 here, in that node. Next, set the new node's references: its next node will be the current next node of the 22 Its previous node will be the 22 node. We generally want to update all of the new node references before modifying the original list so we don't lose references. After that, modify the original list to include the new node: set both 22's next node's previous reference, and 22's next reference to the new node:
node.insert(value)
newNode = new Node(value);
newNode.next = node.next;
newNode.prev = node;
node.next.prev = newNode;
node.next = newNode;
The list looks as follows after making these changes:
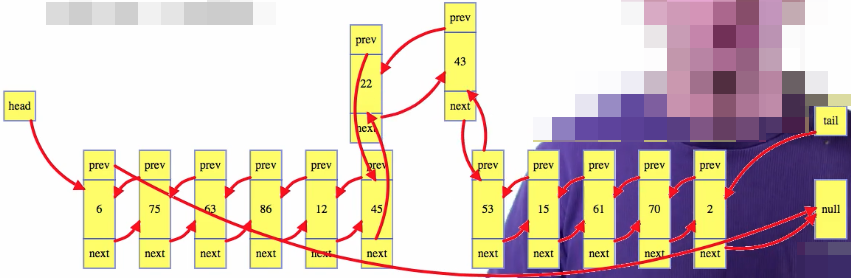
Everything looks nice and neat once we incorporate the new node into the consistent list formatting:
Singly linked lists are the same if we ignore the references to previous nodes. Right now we have some special cases. The code above won't work if we inserting to an empty list, or to the head, or the tail. We could add boundary condition checks for those cases, but if we are willing to use a so-called sentinel node, then we can simplify special cases right out of our code.
Implementation simplification - sentinel node
The sentinel is a dummy node that is used to guard against those special cases. Instead of explicitly storing a head and a tail value for the linked list itself, we just store a dummy node, where the next reference of that node is the head node of the list, and the previous reference points to the tail node. Also, instead of having the tail point to null as its next node, store a reference back to the sentinel node, and do the same for the previous reference from the head:
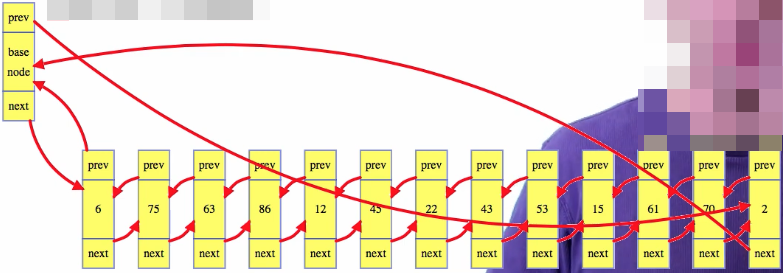
While we still abstractly have a list, the implementation is now more of a "ring", where the dummy node is used to loop from the tail to the head of the list. From the perspective of insertion given a node, there isn't any special location in a ring, so no special case cose is needed to insert at any location, including the head or tail.
The sentinel node lets us fold all edge cases for insertion into the general insertion algorithm, and it also simplifies deletion. It helps for singly linked lists too, but not quite as much because the dummy node won't have a natural place to store the tail reference, so some special cases can creep back in.
Initialize and size
So now an empty list ends up being just the sentinel node, with both previous and next references pointing to itself:
That is how we create a new list. The only other thing we need to store for the list is its size to let us get its size in constant time. Increment the list size during insertion, which is still a constant time operation. As an exercise, we can check that the following insertion code works even when we insert into an empty list, using the sentinel node as the node to insert after:
node.insert(value)
newNode = new Node(value);
newNode.next = node.next;
newNode.prev = node;
node.next.prev = newNode;
node.next = newNode;
(increment list size)
Delete
With our sentinel (i.e., baseNode), we avoid special cases, except the list can't be empty, and we can't delete the sentinel node: it is part of our linked list implementation, but it isn't part of the abstract linked list itself, so it can't be deleted:
node.delete()
if(node != list.baseNode)
Again, imagine that we're magically given a node reference, 86 below, and we want to delete that node from the list:
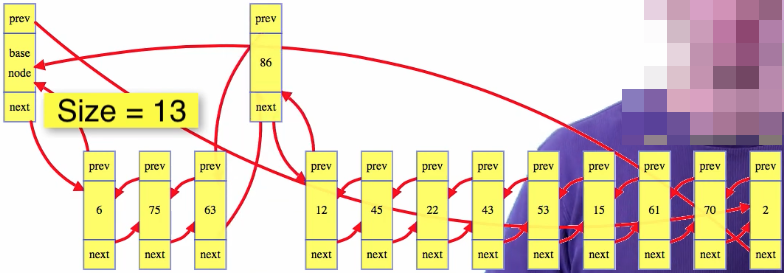
Take the nodes surrounding the condemned node, and stitch them together; above, make 86's next node point to 86's previous node, and 86's previous node point to 86's next node. Then decrement the size of the list and we're done:
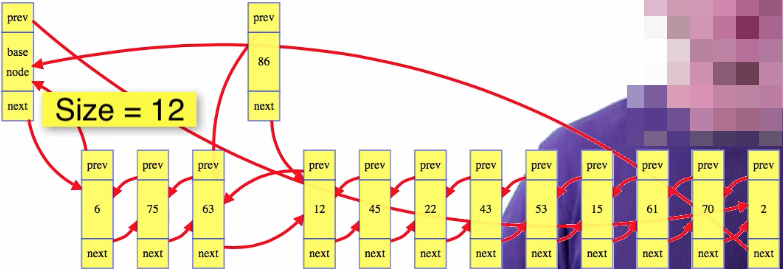
We can throw away 86's references, and do whatever we want with the value itself:
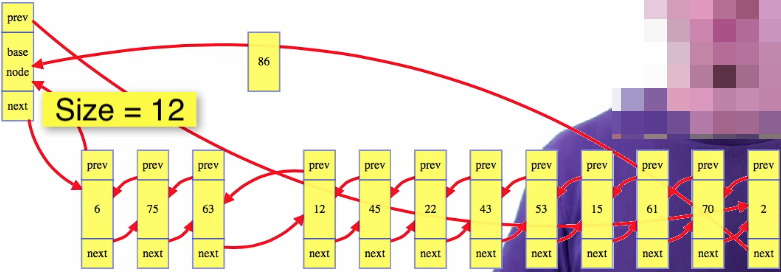
So we have the following for deleting a node from a doubly linked list:
node.delete()
if(node != list.baseNode)
node.next.prev = node.prev
node.prev.next = node.next
(decrement list size)
Singly linked lists are a bit uglier. Instead of a reference to the node we want to delete, we need a reference to the node before it, because we can't efficiently reach from the condemned node back to its previous node to fix that node's next reference.
Data privacy
For the general insertion and deletion we've seen above, we use a node as an argument to tell us where to insert or delete. These versions of insert and delete are for our internal use only, because the outside world have access to our nodes. Keep your nodes private. If you want to give outside users the ability to insert into a special position like the head, then we can just let them call something without an argument, which will then internally call the insertion code with the dummy node for its position. Inserting after the sentinel node will insert to the head position:
list.headInsert(val)
baseNode.insert(val)
When we want to insert or delete to some location in the middle of the list, then users use iterators to store positions, and we still don't let users handle our nodes.
Retrieval and search
The reason we usually use lists to store things is that we care about their order. There are two special locations within that order that we are going to care about most: the first and last terms (i.e., head and tail, respectively). To get these items in a linked list is easy with references to the head and tail nodes.
What if we want to get, say, the 1000th in the list? Well, then we have to walk through the list to get there. Maybe we're clever and our code checks the list size, and if it's under 2000, then it walks backwards from the tail instead of forwards from the head, but worst-case, to get to an indexed location, it takes linear time in the size of the linked list.
Indexed retrieval, indexed insertion, indexed deletion, or searching a linked list — these are all really bad operations. They can all take linear time. Linked lists just aren't built for those operations.
Iterators and traverse
Generally, linked lists are going to work nicely only if we want to retrieve only the first or last item, or else if we want to traverse items in order, which is where iterators can help us. This also explains why linked lists are naturally unsorted structures: the list order itself is important, and forcing the list data to be sorted greatly restricts how we can manipulate the list. It gives little in return.
So the order of a linked list is important, and traversing the list in order is easy using iterators. To implement an iterator, depending on what language we're working in, there should be some mechanism to give users indirect access to anode, while still letting us privately control what that node can do. In Java, for example, our linked list can have an inner iterator class. Objects in that inner class can store nodes as private variables, with full access to the linked list code, but users can only access the nodes indirectly by calling iterator methods. This leaves the linked list abstraction barrier intact, keeping nodes private from the users so they can only manipulate the structure of the linked list through our code.
The iterator privately stores some current node from the linked list. To get to the next node is really simple: just set the variable equal to its next value, assuming that isn't the linked list sentinel node:
iter.next()
if(iter.hasNext())
currentNode = currentNode.next;
Iterating to the previous node is just as easy for a doubly linked list. Iterating forwards or backwards one spot is a constant time operation, and only when we start looping, like for linear search, do we start needing more than constant time. Once an iterator is in the middle of the list somewhere, that's when we can use it for arbitrary location insertion and deletion.
Those are the most basic list operations: creation, size, and an iterator that can move forward or backward one spot, and insert and delete. Each takes constant time. We can also easily implement insertion or deletion from the head or the tail of the list, using a simple wrapper that calls the general insert or delete method with a reference node.
Append
There are less critical but still constant time operations like appending one list to another. Stitch the tail of the first list and the head of the second list together, fix the references to and from the second list tail, and increase the size of the first list by the second list size. The first list now references the combined linked list, and the second list is destroyed. It takes constant time total, replacing the two original lists with one new list.
Split or reverse
We can also have a constant time split operation at a node referenced by an iterator, basically by reversing the append operation, although then the iterator would need to keep track of how many nodes were before its current node in order to properly set the sizes of the two lists after the split. Keeping track of that as we go would still leave all of the individual operations we have seen as constant time each, but iterator indexes will get messed up if we change the list structure after the iterator is created.
We could probably add a few more constant time operations, like reversing the list using a flag to indicate which direction to go, but our code will look a bit uglier.
Dynamic arrays
Arrays
An array is something that holds a fixed number of elements (it's a block of a memory for a group of items). For notation, an array has some variable name and then has a numerical index position inside of some square brackets. For example, stuff[4] would denote the 4th position within the array.
Some languages use this same notation but allow us to index by anything, like a string, but that's mostly interesting from a trivia standpoint. A "real" array is implemented as a continuous block of computer memory. We could start numbering at 1 (this is often the case in textbooks and academic papers), but we'll start at 0, which is most common in different programming languages. Thus, an array of size 8 has items indexed from 0 to 7:
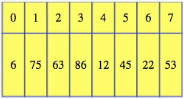
We can store whatever we like in the array, but the size of each item is the same. So, we can have an array of integers, or characters, or object references, or even fixed-size objects. Some of that is language-dependent, but abstractly, just imagine a bunch of items lined up in some fixed amount of memory that has been allocated to our program. The great thing about arrays is that they give direct access to any location. Like any variable, the array name is associated with a memory location, and then the index just gives an offset from that location to a new memory location. If we want the fourth item, then we just move forwards by four times the size of each item in the array:
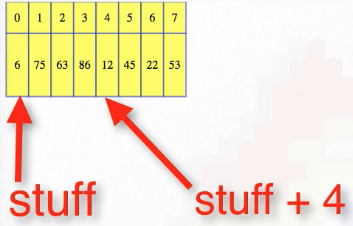
We'll use integers here, so we just move forwards to get the fourth integer after the one that starts the array. This is a very quick operation. Because arrays map directly to our computer memory, we need to specify how large the array will be when we allocate memory for it. This is clearly a weakness: sometimes we don't know how many spaces we need. If we don't allocate enough spaces, then we'll run out of room, but if we allocate too much space, then we waste memory.
Dynamic arrays
The big idea behind a dynamic array is that if we want to add something to an array that is already full, then we just allocate a bigger array, copy over all of the items from the old array, and we have space for more elements. Genius, right?
No, it's really simplem, but we need to do it the right way to get good performance. A bad way to go would be to just allocate exactly the space we know we need right now. So, for the example above, if we needed room for a 9th element, then we could copy over everything into an array with 9 spaces:
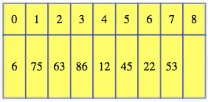
But later if we wanted to add a 10th item, we would then need to move to an array of size 10:
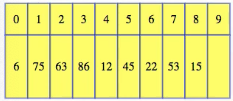
This kind of hyper-conservative approach can really be problematic in the long term. To add the th item takes time proportional to , so if we add total items, then it takes time. A better way is to make the new array proportionally bigger than its current size, even if that's more than we immediately need.
Insertion and growing
Starting with the size 10 array above, when we run out space, we could double the array size. So once we realize that we have an 11th item and our array only has 10 spaces, then we allocate a new size 20 array, copy over the first 10 items, and then add the 11th:
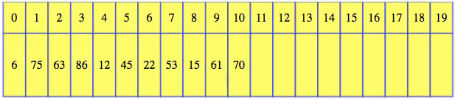
In code, this looks something like the following:
insertion(val)
if(size == capacity) {
capacity = 2 * capacity
newStuff = 2 * capacity
newStuff = new Array[capacity]
for(i = 0; i < size; i++)
newStuff[i] = stuff[i]
stuff = newStuff
}
stuff[size] = val
size++
We keep track of the fact that our data structure has size 11 but capacity 20. Now, there's still room in the array, and if we want to insert a 12th item to the end of the data structure, then just stick it there and increment the size:
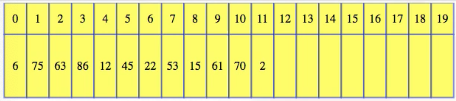
For this data structure, by default, always add new elements to the first unfilled location. We don't allow skipping, and if we add it to an earlier location, then we have to shift items over to make room for it, and it kills our performance.
While inserting only to the end is a bit of a limitation, the underlying array structure does let us directly access any item in constant time. If the size is less than our capacity, then we can also add or delete from the end of the list in constant time too.
Bad insertion
Of course, if we really want to insert to somewhere in the middle of the array, then we can, but it takes time proportional to the number of items after the position we're inserting to because we will shift all of those items over to make room. Deletion from the middle also forces a shift to fill the blank space. Insertion and deletion from the middle of the array aren't really natural operations. They force us to loop over everything after the changed location.
The ArrayList class in Java has methods for indexed insertion or deletion, but it is internally implemented with a loop. They may have optimized that loop to try to make it fast, but we shouldn't forget that it's there nonetheless. The default position for inserting or deletion is the end of the list.
Analysis intuition
What happens if we want to insert to the end, but the array is full? We can't just stick the item in place and increment the size anymore. Instead, we need to allocate new space, copy all of the items over, taking linear time, such as going from
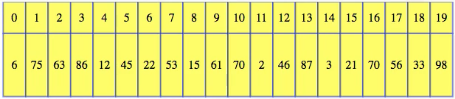
to

Can we fix that? Well, it turns out that we don't need to. Because we double the array size when growing, those expensive insertions can't happen very often. Inserting to the end is expensive when going from size 10 to 11, but then we get a whole bunch of constant time insertions to go all the way up to 20. Then we get another expensive insertion, twice as expensive as the previous one, but then we get cheap insertions all the way up to 40. Some insertions are expensive, but on average they take constant time each.
Amortized analysis definition
This is called amortized analysis: instead of looking at the cost of each operation individually, we consider the total runtime for an entire sequence of operations, and use this to get the average performance per operation. For this data structure, the average performance of inserting to the end of the list is constant time. We can look at the best case average performance per insertion or the worst-case average performance, or even the average case average performance. They are all constant time.
Amortized analysis - accounting method
How do we prove that insertion takes on average constant time per operation? Going back our half-full array of capacity 20, imagine that every time we insert into the array, if we have space, we not only pay for insertion, but also prepay to copy 2 values to a new location sometime in the future. Including this extra imagined payment, insertion still takes constant time, even if it's a few times larger than the real time insertion takes. Clearly, adding that extra time to our time analysis isn't going to let us undercount how much real time is used to insert items.
When go to insert the 21st item, we first allocate the new array, size 40, and copy over 20 items to it. But, for those last 10 insertions we did, we have already included the cost of 2 copies each in our time analysis. In our analysis, we withdraw against our prepaid copy operations, and we have already deposited enough to copy over all 20 items. The actual copying doesn't happen until now, but if we're analyzing all of the time spent from the beginning, then we see that we've already accounted for the time of these copies during the last 10 insertions. For the 21st item, we only still need to pay for its insertion, and with it we'll also prepay for two copy operations for the next time the array grows.
This is called the accounting method for amortized analysis:
- For each below capacity insertion, count its cost plus ... prepay to copy it and a friend, at a later time, to a new array.
- For a full capacity insertion, cost of copying has already been counted.
Our analysis overcharges for some operations and uses those prepaid overages to pay for expensive operations which may come later. As long as the analysis for any sequence from the start charges at least the real life amount, we can use it to get valid average upper bounds.
Deletion and shrinking
How about deletion? If we want to delete from the end of the list, then clearly we can do that in constant time, but is there any reason to shrink the size of the underlying array if it's "too empty"? Before figuring out how to do that, is it really worth doing? It is (not shrinking wastes space, especially for multiple lists).
Imagine that we're simulating a set of a billion items moving around between a thousand lists. On average, the lists have a million items each, but occasionally, maybe most of the items end up being in one list. When that happens, the list size will grow to hold a billion items. If different lists are crowded at different times, and we never shrink any of them, then eventually we end up trying to allocate a thousand arrays of size a billion each, even though we only have a billion items.
More generally, if we never shrink, then lists holding items total can take space, when it should be space. So when should we shrink the arrays? First of all, it depends on our growth factor when we grow our arrays. We have been using growth factor 2 so we can't shrink them if they just go under half full or we could end up with a bunch of expensive operations if we ever alternated between inserting and deleting right near a boundary, like between sizes 19 and 21 for our example. It would be slow. But if we double when growing, but only shrink when we go under, say, one quarter full, then we'll be safe. Maybe have some minimum size too.
Using similar analysis to the insertion, where every deletion deletes one item from the end of the list, but we also prepay for a copy operation, we can prove that each deletion also takes amortized constant time. If we implement shrinking, then array lists use only linear space in their size.
Natural operations
Now that we know how array lists are implemented, it is easy to see what operations they give and also how to make an iterator for them:
- Insert (to end)
- Delete (from end)
- Access (by index)
- Iterate (without insertion or deletion)
- next
- prev
They support constant average time insertion and deletion from the last position as well as constant time indexed item retrieval. Because of that quick retrieval, to make an iterator, the only information we need to store is an index, but we the iterator shouldn't really be used to mess around with the middle of the list by inserting or deleting there.
Advanced dynamic arrays
Storing objects
From an abstract, black box, don't worry about constants point of view, there isn't too much difference between directly storing objects compared to storing object references or pointers (arrays generally store objects while linked lists store references):
But when we get into optimization issues, it matters. We start by assuming this former model that the data is sitting within the array itself (top image above). We already know that this data structure uses linear space and has average constant time insertion and deletion to the end of the list. But, of course, those constants can vary. Previously, to make the analysis easy, we doubled the size when we grew the array, and right after that, we're using about space to hold items. Then, if we delete items until just before the data structure shrinks, which we've said we'd do when we got down to the one quarter level, we can get down to using only a quarter of our array which is a bit wasteful of our memory. We can be wasting three quarters of what we're reserving. Those numbers are somewhat arbitrary. If we wanted, we could grow the array by only 50 percent, instead of doubling it, and maybe shrink by one third when under one half full. That decreases the memory overhead of our data structure. It will always use at least half the space reserved instead of only a quarter, but there is a tradeoff.
Space vs. time
Modifying the insertion analysis for this smaller growth factor, each insertion now has to pay for 3 future copy operations instead of 2 to make our insertion analysis work out. Deletions now need time for 2 future copies instead of one. Because we end up doing our expensive operations of reallocating and copying into a new array more often, the average amortized time per deletion and insertion goes up.
This space vs. time efficiency tradeoff is really common in algorithm and data structures, and by changing our load factor, growth factor, or whatever we want to call those numbers we picked, we pay with one to optimize the other. It's hard to simultaneously master both space and time. That's a pretty abstract and theoretical.
Memory management
Let's dive into more concrete memory management issues.
Semi-automatic memory management
If we are manually managing our own memory heap, then good luck. If we're using a language like C, then we will call this semi-automatic memory management. We allocate memory by request, and manually free it when we are done, but we don't decide which memory block to allocate. It also has the realloc function, which we will come back to.
The following array represents our memory:

Some of the memory is in use, but we're assuming that the light colored stuff is currently unreserved. It might be empty, it might have some left over junk in it, but it's part of the memory available to, but not currently used by, our program. So, starting with a little growable array of size 4, the memory system gives us a block with enough space to hold 4 elements:

For the diagram above, each element takes up to 3 units of memory. So great, insert, and when the array is full we insert again. For simplicity, let's use growth factor 2.
Suppose we call the realloc function, requesting room for 8 spaces. In this case, it looks just like a normal allocation: it allocates new space:

And then it copies over the old data as quickly as it can (it's really optimized code):

And then it frees the old space:

It can leave that old data just sitting in memory, but that memory is no longer reserved, and it can be used for something else. The real difference comes when we grow this array past size 8:

In this case, the space immediately after the array isn't reserved right now, and when we go to realloc to a size 16 array, there is enough room to just extend the current array size to 16:

In this case, we don't need to copy anything over. The data from our old array is still being used, just with added capacity. When that happens, we get lucky, and one of our potentially slow insertions takes constant time instead of linear time. If our structure is dominating the memory used by our program, then maybe this will happen a lot.
Automatic memory management
Well, what if memory management is more automatic, and we are forced to allocate a new array each time, with little control over what memory is allocated? If our memory manager just allocates the first big enough block of memory that it has, growing by a factor of 2 has an extra disadvantage. Let's return to our big strip of memory:

Each time we ask for a new array, we just take the earliest one available, doubling in size each time. Even though we keep freeing up memory from our old arrays, there will never be enough freed memory to use for a new array that we are allocating, even if nothing else gets in the way. Below, when we go to allocate a size 32 array, we just don't have space for it, even if we have enough memory for, say, 60 total items:

We've freed room for 2 + 4 + 8 = 14 items, but even if we were to include the 16 items we are about to free up, there just isn't room -- we're going to extend past those 16 items. But, if we take the 14 + 16, that's 30 items; maybe there's only room for 30 more items after that, there's not room for 32 items there either. The 16 items can't be freed up until we copy them — they are right in the middle, and basically we don't have room for the 32. We never reuse our space, and we end up unable to allocate more space even though we're barely using 1/4 of our memory, and nothing else is in our way.
If we have a growth factor under the golden ratio, about 1.6, then we guarantee that eventually, if nothing else gets in our way, we can reuse freed space for our new array. Here, for our 5th allocation, we get to reuse space. If we go down to a growth factor of about 1.32 (the solution to some cubic formula), then the two previous arrays, already freed, prior to the one currently in use, will have enough room for the next array we allocate.
In this example, as things progress, with nothing else getting in the way, we'd expect every third allocation to go right back to the start and move on from there.
Storing objects vs. references
Let's finish by considering the case where store object references in the arrays instead of directly storing objects:
From a speed factor, directly storing objects is going to be much faster for accessing items, especially if we look at them in order. Sequential access of arrays is highly optimized: we have locality of reference, we might even be able to prefetch data. Locality of reference will also help us if our data is stored to disk. If we get a page of data from disk, and we're looking at data in order, we bring a whole bunch of stuff we're about to need into memory all at once.
Additionally, if the objects are small, the extra space overhead of the references themselves might be something we care about. There can also be some other issues causes by allocating lots of small objects.
What are the advantages of storing references instead of objects? As the objects get larger, there are a few. The simplest one is that when we need to reallocate to a larger array, it's easier to copy over small references instead of huge objects. Also, the unused capacity within the array, it's better for that to be wasting room for just small references instead of large objects.
Finally, if we start dealing with large numbers of large objects, where total memory gets to be an issue, then storing references has one important advantage. It needs one block of memory for the array of small references, but the individual objects can be spread all over our memory. Trying to get faster performance by storing a big block of objects doesn't get us anything if we can't get a big enough block of memory to do it. For segmented memory, maybe there's enough room to fit the objects we need if they are scattered all over the place, even if there isn't room for one big continuous block of memory holding all of the objects.
It's the flip side payoff for that slower access. We get to sort of use all of the memory we have filling in all the gaps with our objects because they're all over the place.
Linked lists and dynamic arrays - misuse and abuse
API PI
There's mentioning of how Java gives us great LinkedList and ArrayList classes with APIs that do tons of stuff, but we have to look behind the scenes if we want to use them correctly. For instance, for linked lists, the docs tell us the following:
All of the operations perform as could be expected for a doubly-linked list.
So we need to think about how linked lists work in order to avoid methods that work badly. For example, suppose we want to know whether or not an item is in our linked list. Then we could do a slow, linear search to see if it's there. But we don't have to write that slow code. Slow code has conveniently been provided for us (i.e., the contains method). The contains method in the API looks nice, and it's tempting to use without thinking about performance. But if we had to write that loop ourselves, then we might stop and wonder if that's really the data structure we want.
Strengths
We should think about what both approaches do well. They can add to, remove from, or look at the end of a list, look at the front of a list, and return an iterator that can traverse the list in either direction in constant time per element:
- insert at end
- remove from end
- inspect end
- inspect start
- size
- iterate forwards or backwards
That's basically it. Each structure also has some extra ability. Linked list iterators can add or delete elements from their location in the list, and arrays give us direct access without inserting or deleting:
- Linked lists:
- insert at iterator
- remove from iterator
- Dynamic arrays:
- access by index
- setValue by index
Those functionalities complement each other. The linked list can be coded by just coding its iterator and tracking its size. All of the other linked list methods come from just manipulating its iterators. On the other hand, the array structure has all of the methods really coded in there, but its iterator doesn't need any special access, its functionality comes from just keeping track of an index and then calling ArrayList methods.
Finally, it should be mentioned that the constants tend to greatly favor the array-based methods. That's even more true in languages where we can store the objects instead of references to the objects. That isn't exactly a new method, but it is a strength.
Summation example
Let's start with a simple example. Here is some bad code to run through a list and get a sum:
sum = 0
for(i = 0; i < myList.size(); i++)
sum += myList.get(i)
return sum
This is one that both structures can do well, but if we're lazy, we can really hose ourselves. The code above with an ArrayList works great. Behind the scenes, this get method uses direct array access. But then we test it with a LinkedList. Behind the scenes, the get method is actually a loop on an iterator, and the performance sucks. Instead, if we properly use an iterator, then both structures work well:
sum = 0
tmpIter = myList.listIterator()
while(tmpIter.hasNext())
sum += tmpIter.next()
return sum
The ArrayList uses the iterator to look up an index for direct access, and the LinkedList uses the iterator to go through the list once, instead of making a new iterator per item.
Filter example
Now suppose we have a list and we want to, say, filter out and remove all odd numbers. With a linked list, that is fine — we iterate through the list once, and sometimes delete stuff. But for each of these deletions, the ArrayList shifts over all of the items after it. If we happen to delete every other item, then the LinkedList will take linear time, the ArrayList quadratic. We'd be better off creating a new ArrayList out of the elements we want to keep than deleting all contents from the original ArrayList, and then refilling it with stuff from our new list.
Sorted list example
Now suppose we have a list, and we only insert to the end of it, and every inserted value is bigger than the previous one. Here, the items are in sorted order. To search the list for items, we can always do a linear search, but for the array-based model, we can use binary search which takes only logarithmic time. But if we were so foolish as to use binary search on a LinkedList, each of those logarithmic number of accesses could take linear time, so it can take to find if an item is in the list. Worse than linear time! That's fantastically bad.
Advice
When the APIs look so similar, or when we use the List interface (in Java), we have to be careful not to use methods that are inefficient for the structure we are using, even if they are good for the other one.
- Know how the data structures work, or at least the efficiency of each method.
- Know which methods are natural, and which ones are just for convenience.
Having the same methods for the two APIs of ArrayList and LinkedList makes it really easy and convenient to write inefficient code without realizing it. It might be better if some of those methods weren't there.
Ultimately, here's some good advice to hang your hat on: Think about the code hidden behind convenience methods. Don't use those convenience methods unless it would have made sense for us to write that code in that place.
Stacks, queues, and double ended queues (deques)
Stacks
Stacks hold items in a Last In, First Out (LIFO) order. Whenever we take something from the stack, we get the thing that was put into the stack most recently. We talk about the top and the bottom of the stack, and the idea is that if we have a stack of things, and we want one, then we take one from the top, and when we add to the stack, we add to the top.
For a non-empty stack, the bottom doesn't change. For a stack, inserting and deleting are traditionally known as pushing and popping. We might also have some other operations, though of these, only size gives us something that we don't get easily from push and pop. We can simulate peeking by popping and then re-pushing an element, and when we do that, if there isn't anything to pop, then we know the stack was empty.
Let's recap the key stack operations:
push(element): Adds elements to top of stack.pop(): Removes and returns element from top of stack.- Optional:
peek(): Returns element from top without removing it.isEmpty(): True if and only if stack is empty.size(): Returns size of stack.
Queues
Queues, on the other hand, hold items in a First In, First Out order. When we remove something from a queue, we get the thing that's been there the longest. This is often likened to the process of "getting in line" or queueing up — we move towards the front of a queue, from the back or rear, and traditionally, insert and delete are known as enqueue and dequeue. Note that, for a queue, peek() does give us a new ability, which can't be easily replaced by dequeue and enqueue, because once we're out of line, we have to go to the back to get back in.
Let's recap the key stack operations:
enqueue(element): Adds elements to back/rear of queue.dequeue(): Removes and returns element from front of queue.- Optional:
peek(): Returns element from front without removing it.isEmpty(): True if and only if queue is empty.size(): Returns size of queue.
Double-ended queue (deque)
For deques, operation names aren't standardized. Knuth calls the two ends left and right, and we'll call the operations insert and delete, but all kinds of different names are used:
insertLeft(element): insert element into leftmost position.insertRight(element): insert element into rightmost position.deleteLeft(): Removes and returns leftmost element.deleteRight(): Removes and returns rightmost element.- Optional:
size(): Return size of deque.
It's pretty clear that if we somehow have a deque implementation, then that automatically gives us a queue or stack implementation pretty easily. But, in some cases, stacks, or even queues, can have somewhat simpler underlying structures.
Linked list implementations
Deque
Doubly-linked lists give a really easy way to implement deques:
We can insert or delete from the head position, call that the left, and we can insert or delete from the tail position, call that the right. Done. Even with the optional size and peek operations, all operations take constant time.
Queue
For a regular queue, a singly-linked list with tail reference will do:
Stacks
Stacks are even simpler. We can use that singly-linked list without even keeping a tail reference. Just push to and pop from the head location:
Array-based implementations
Stacks
Let's start with the simplest structure to implement with arrays, namely stacks:
We can directly use our dynamic array to implement a stack: we know it can insert to or delete from the array's last position in average constant time. If we just call that last position the top of the stack, we are done.
Queue
For queues, things get a bit more complex. There might be a few different array-based approaches, but we're going to use circular arrays (i.e., circular array within structure using dynamic array logic). They're simple and elegant, but still efficient. Instead of using a prepackaged dynamic array like ArrayList, we instead build a new data structure from arrays, but we use the same ideas and analysis that were used to build dynamic arrays. So like dynamic arrays, we allocate an array with a fixed capacity, keep separate track of the size of our structure within that array, and reallocate when our size grows beyond that capacity. Really the only changes are that we won't force the first element of the array to be in the first location within the array, and we will allow ourselves to wrap around when we get to the end of the array if the first position isn't being used.
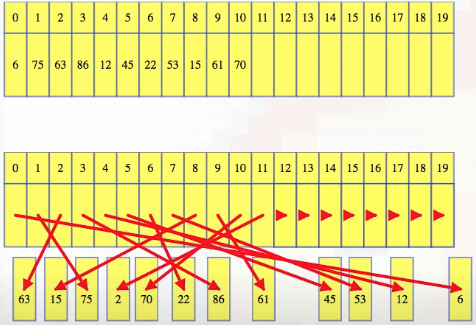
So for queues, when we enqueue, we start by adding to the end of the array, just like normal, and if we enqueued right past the capacity of the array, it would look just like our growing dynamic array. But at some point, we dequeue. We return and remove the first element, but instead of trying to shift everything towards the front of the array, instead, we shift the logical start of the queue over by one:
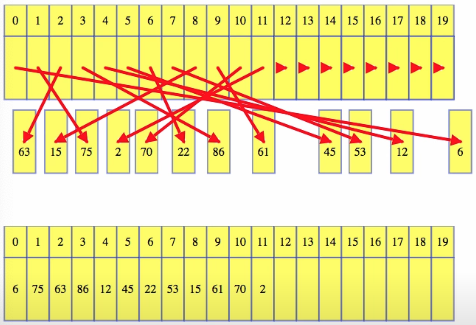
Dequeue again:
After doing that a few times, the front of the queue moves further back within the array. Next, if we enqueue up to, and then past the end of the array, then just wrap to the front of the array and add the element there:
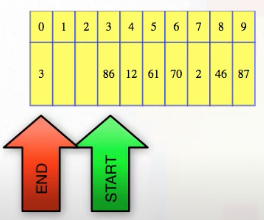
If we do our increments and indices modulus the capacity of the array, then the calculations are really simple. Resizing is like in dynamic arrays, except we always copy the logical starting index to the new array location 0, and wrap around in the old array when copying from it as needed The new array will have everything indexed nicely from 0 when it's first created:
enqueue(item) {
if(this.size == this.capacity) this.resize();
this.array[this.startIndex + this.size++ % this.capacity];
}
dequeue() {
if(this.size == 0) core.dump();
if(this.size <= this.capacity * minLoad && this.size > this.minSize) this.resize();
tmp = this.array[this.startIndex];
this.size--;
this.startIndex = (this.startIndex + 1) % this.capacity;
return tmp;
}
Deques
For deques, the same logic works, we just need to rename enqueue to insertRight, dequeue to deleteLeft, and then write symmetric insertLeft and deleteRight methods that will sometimes wrap the index from the first position of the array back up to the last one.
