Binary heaps (with attitude)

This post explores binary heaps, including what they are, a linear time method for building a heap, heap sort, binary heaps for priority queues, and optimized heapify.

Attribution

The notes below come from the Algorithms with Attitude YouTube channel, specifically the Binary Heaps playlist comprised of the following videos: Introduction to Binary Heaps (MaxHeaps), Linear Time BuildHeap, Heap Sort, Binary Heaps for Priority Queues, and Optimized Heapify.

There are several sections in this post, accessible in the table of contents on the right, but most of the sections have been listed below for ease of reference and navigation.

• Introduction to binary heaps - MaxHeaps
  • Heap structure
  • Heap shape
  • Heap property
  • Heap representation
  • findMax operation
  • insertion and bubble
  • Deletion and heapify
  • Efficiency
• Linear time BuildHeap
  • Iterated insertion
  • Iterated insertion analysis
  • buildHeap operation
  • Informal analysis
  • Exercise
  • Clever analysis
• Heap sort
  • Overview
  • buildHeap() phase
  • deleteMax() phase
  • Analysis
• Binary heaps for priority queues
  • maxHeap vs. minHeap
  • Objects vs. references
  • Priority queues
  • Operations
  • changeKey
  • delete
  • The catch
  • Options
• Optimized heapify

Introduction to binary heaps - MaxHeaps

Heap structure

Binary heaps are rooted binary tree structures with two special properties. The first property is the shape of the heap. It is going to be a perfectly balanced binary tree where every non-leaf has exactly two children, and all of the leaves are at the same level. It gives us this great shape:

It gives us that perfect shape if we happen to have exactly the right number of nodes to make a perfectly balanced binary tree. Instead, we can have an arbitrary number of nodes, where the last nodes are going to be filled in, on the bottom, from the left:

Such a tree is called a complete tree. When we have an even number of nodes, 32 in the case above, we have one node which has only one child instead of two. But, once we insert another node, we are back up to an odder number of total nodes, 33 in this case. Every non-leaf has exactly two children. We can fill in as many nodes as we want.

We are always filling in from the left on the lowest level, and we get a nice shape:

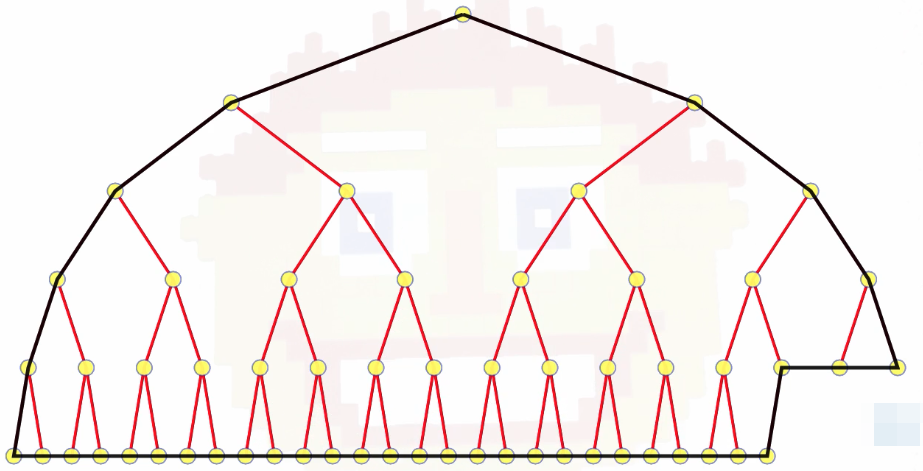
That's the entire parent/child structure of the heap.

Heap shape

But, it doesn't really give a great impression of the heap's shape, because every level of the heap has twice as many nodes as the level above it. So if we want a more accurate intuition for what the shape of the heap should be, it's more like the following:

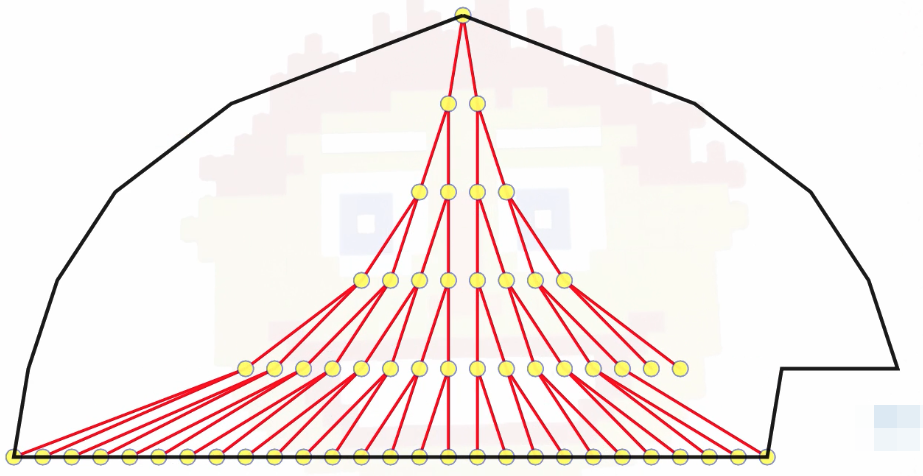
The above gives us the full structure and shape of the heap.

Heap property

Let's now talk about this thing we'll call the heap property. It goes by a different name in some texts:

• Brassard and Bratley: heap property
• Cormen, Leiserson, Rivest, and Stein (CLRS): max-heap property
• Dasgupta, Papadimitriou, and Vazirani (DPV): special ordering constraint
• Kleinberg and Tardos: heap order
• Sedgewick: heap condition

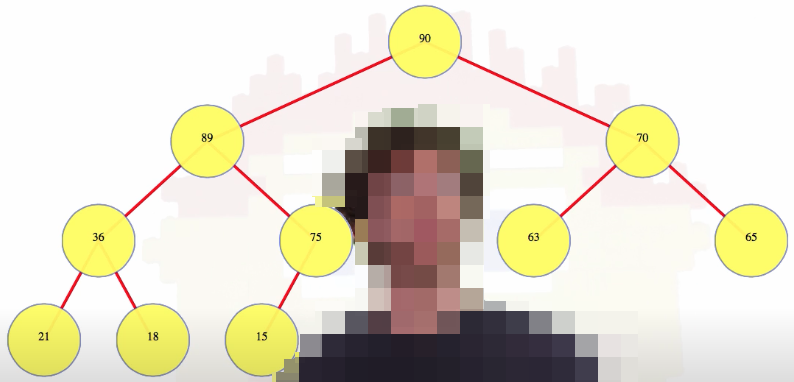
To discuss the heap property, we're going to have to look at some actual values in the tree. A heap is an abstract data type (ADT), and we can store whatever we want in it, but for our purposes, we're just going to look at with some integer keys:

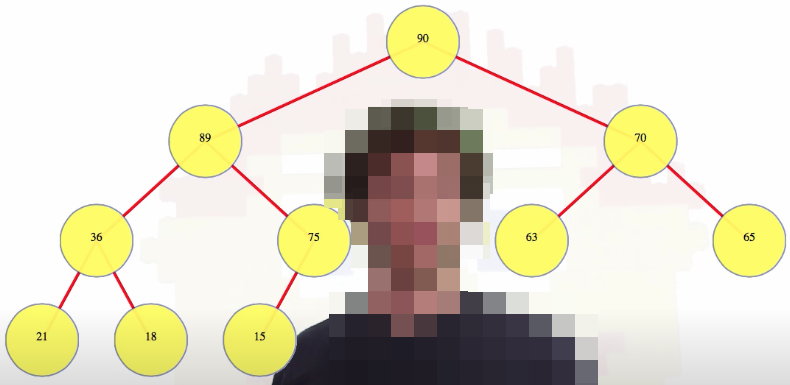
The (max) heap property says any node (e.g., the root) has a value at least as large as the values in that node's children (e.g., 89 on the left and 70 on the right). Note the recursive nature of the tree structure above. The heap property needs to be true for every node.

Sometimes one child will be bigger than another, but there's no left/right orientation. For example, the root node, 90, has its left child bigger than its right child: 89 > 70. And 89's right child is bigger than its left child: 75 > 36. That's okay.

Also notice that 75, even though it's on a lower level of the heap, has a larger value than 70. That can happen as long as 75 is not a direct descendant of 70.

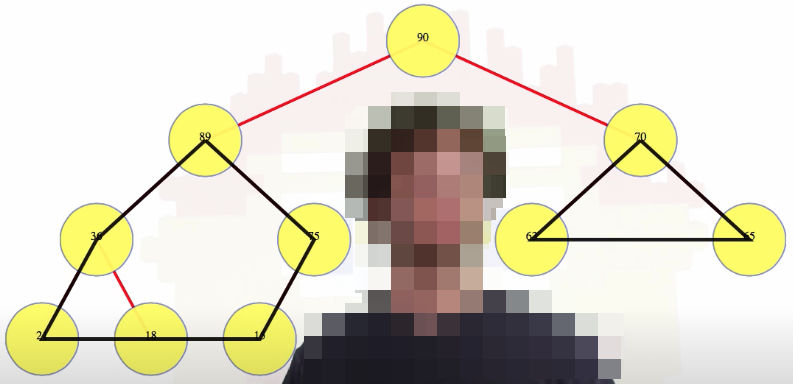
This is the second property we referred to previously: the first property is the shape and the second property is what we just discussed. If we have those two properties together, then note that we get something nice: every node is actually the root of its own subheap, which has the right shape, has the right values, and everything is nice:

Heap representation

We now need to talk about heap representation, specifically explicit vs. implicit representation.

The shape of a heap is so normal that we can really represent it nicely. We know, for instance, that every heap with 10 nodes has exactly the shape of the heap below:

And the 10th node is the left child of the right child of the left child of the root. Phew. What we're going to do is we are going to use an array to store all of the heap values. We're going to store them top to bottom, left to right:

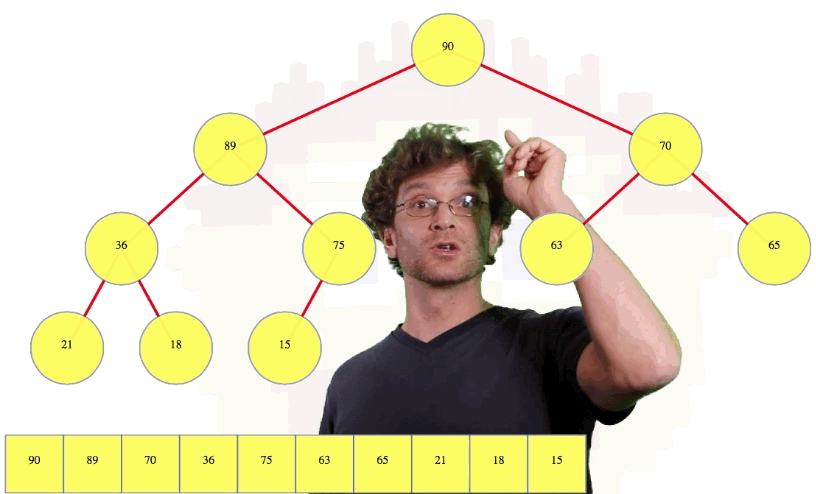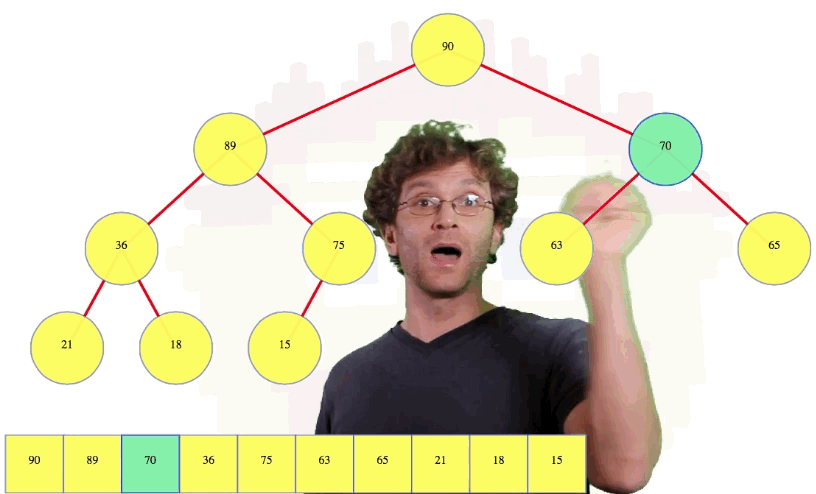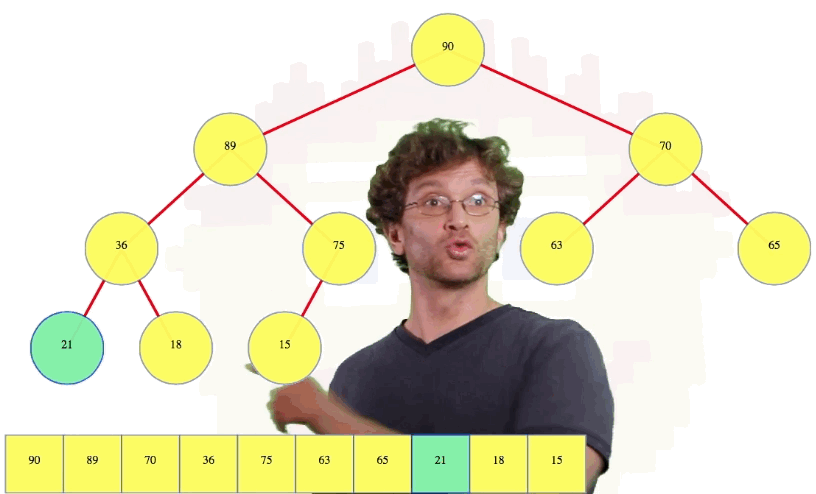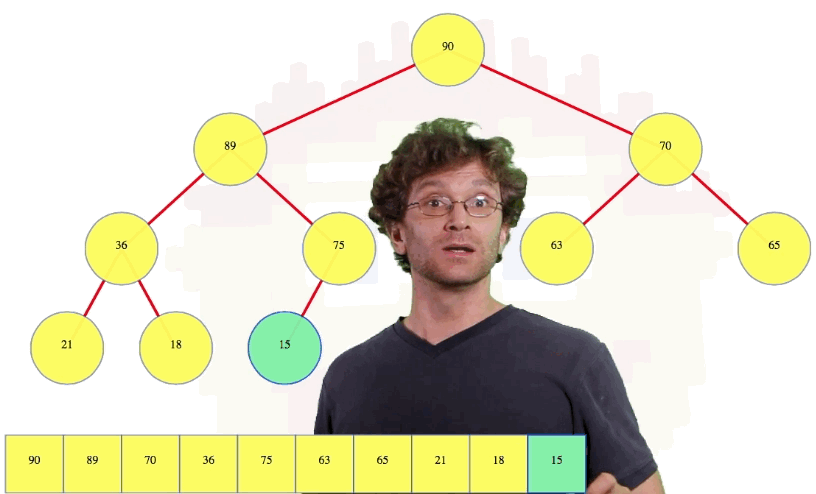
We know, in this case, the 10th (i.e., 15) value is going to be the 10th value in the heap.

We're going to use the indices of our array to describe the parent-child structrue (this is the implicit heap description). If, for instance, we are indexing from $1$, then the left child of index $i$ is at index $2i$, and the right child of index $i$ is at index $2i + 1$; furthermore, for any arbitrary node, the node at index $i$ has the node at the following index as its parent: $\lfloor i/2 \rfloor$:

Indexing from 1:

i _left_    = 2i
i _right_   = 2i + 1
i _parent_  = floor(i / 2)

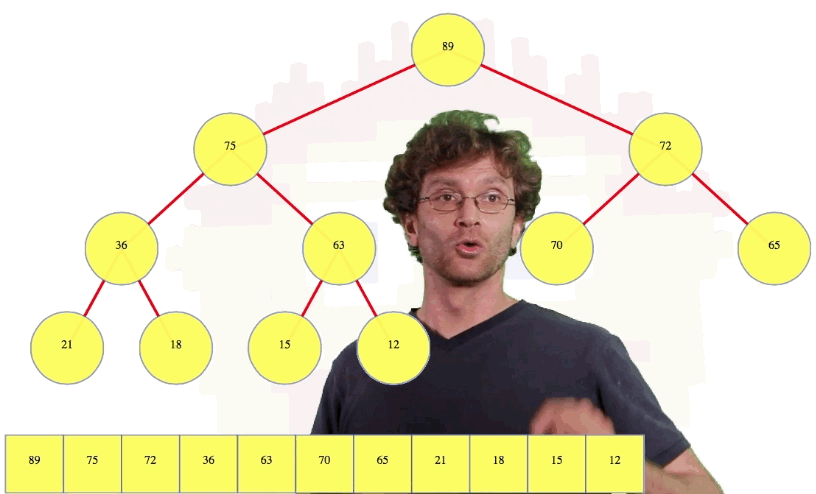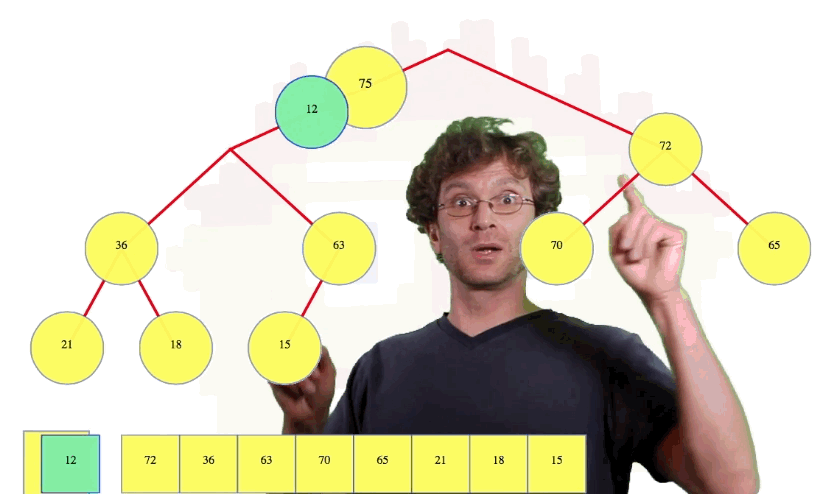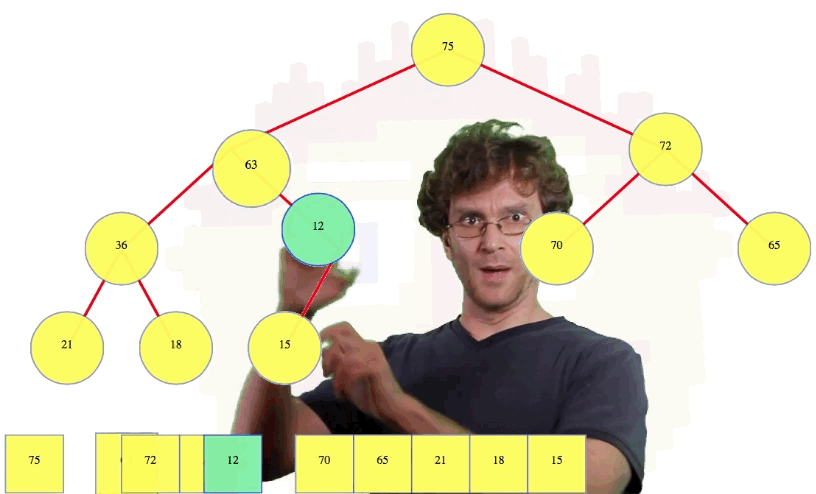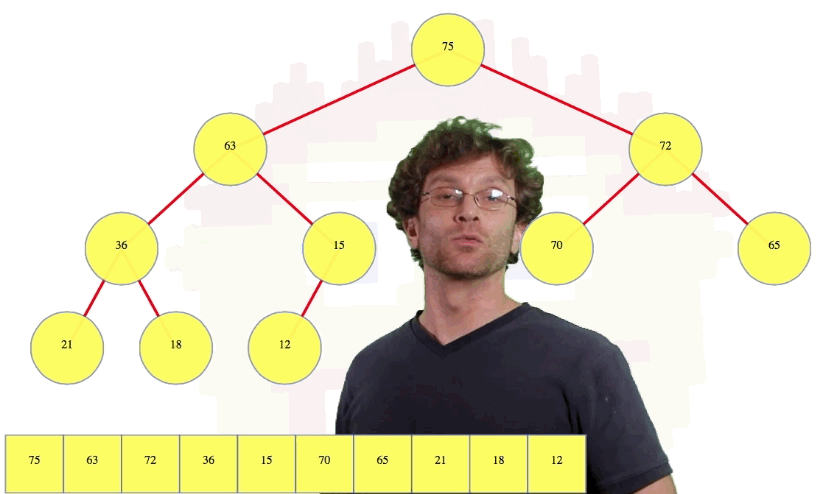
For example, in the previously pictured tree, node 70 is at index 3. Its left child, 63, is at index 2 * 3 = 6, and its right child, 65, is at index 2 * 3 + 1 = 7.

If, however, we're indexing from $0$, then the left child of index $i$ is at index $2i + 1$, and the right child of index $i$ is at index $2i+2$. For an arbitrary node at index $i$, that node's parent is at index $\lfloor (i - 1) / 2 \rfloor$:

Indexing from 0:

i _left_    = 2i + 1
i _right_   = 2i + 2
i _parent_  = floor((i - 1) / 2)

findMax operation

The operation for finding the maximum in a max heap goes by different names according to different sources:

• Cormen, Leiserson, Rivest, and Stein (CLRS): HEAP-MAXIMUM
• Dasgupta, Papadimitriou, and Vazirani (DPV): special ordering constraint
• Kleinberg and Tardos: FindMin (minheap)

We'll call this operation findMax. Finding the maximum node in a max heap is going to be the easiest operation we have because it's directly accessible from the root.

insertion and bubble

• Brassard and Bratley: insert-node, percolate
• Cormen, Leiserson, Rivest, and Stein (CLRS): MAX-HEAP-INSERT, HEAP-INCREASE-KEY
• Dasgupta, Papadimitriou, and Vazirani (DPV): insert, bubbleup
• Kleinberg and Tardos: Insert, Heapify-up
• Sedgewick: insert, upheap

The next operation we are going to talk about is insertion. It's probably not the most important operation for a heap, but it's really easy. We know what the shape of the heap has to be after we insert, so we are just going to insert a value, and if we happen to insert a value in the previously pictured tree, say, 12, and if it's smaller than the last value in the heap, then we're done:

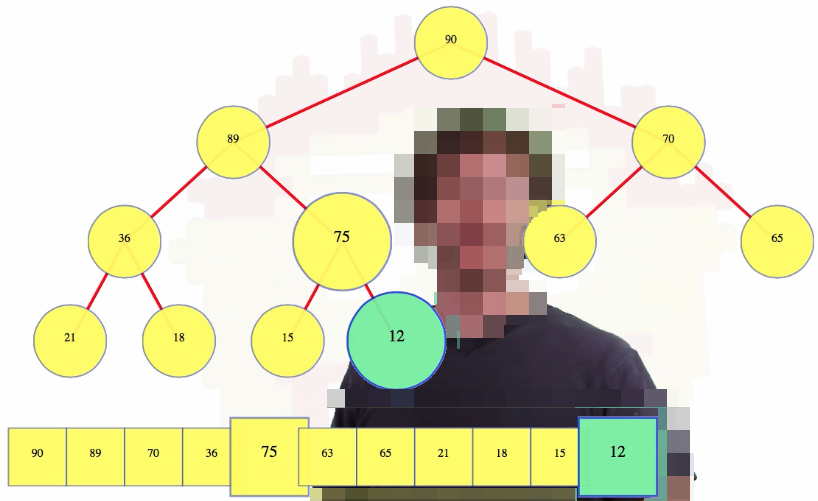
But what happens if we insert a larger value, say 72:

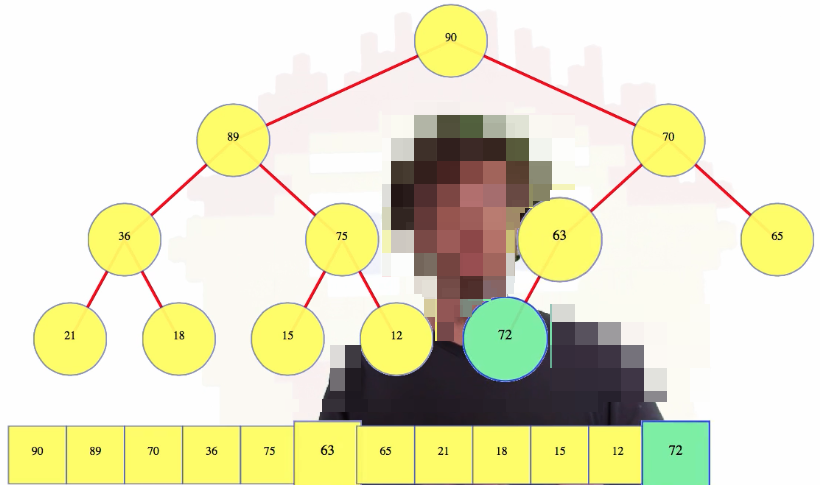
We compare 72 to its parent, 63. Since 73 is bigger than its parent, they swap. Now 72 is still bigger than its new parent, 70, so we swap these values too. When 72 is compared to 90, the root, we see that 90 is bigger than 72, so that is where the swaps end. Whatever node we insert just keeps moving up until we're done

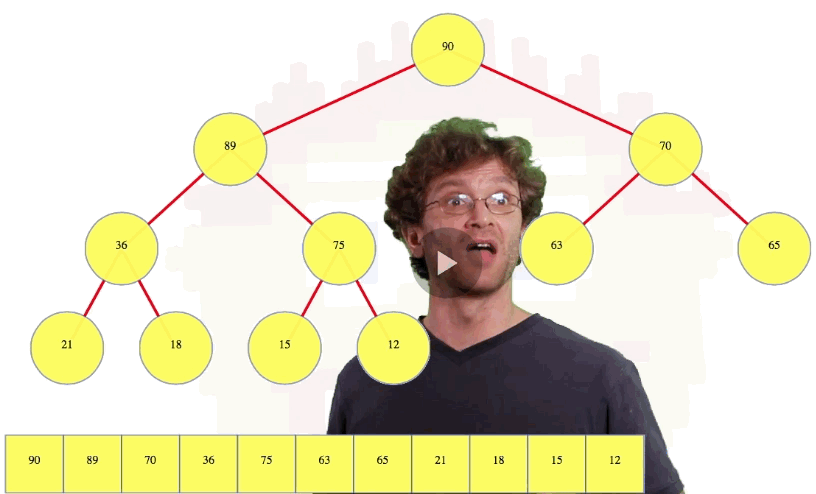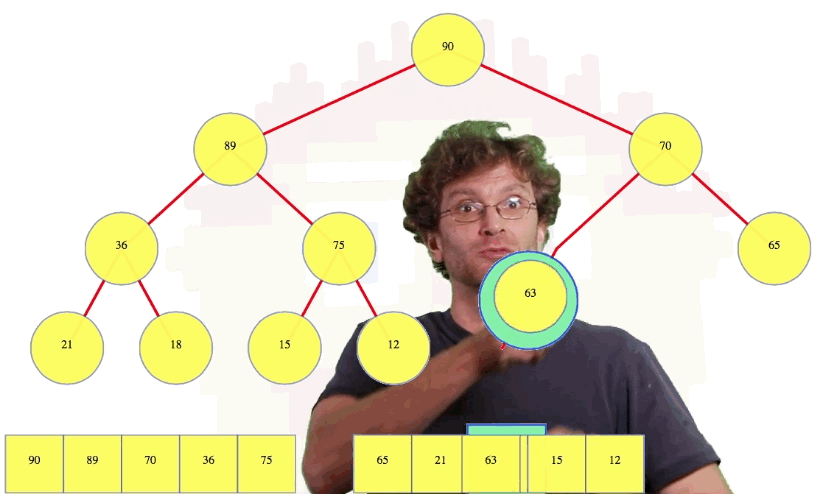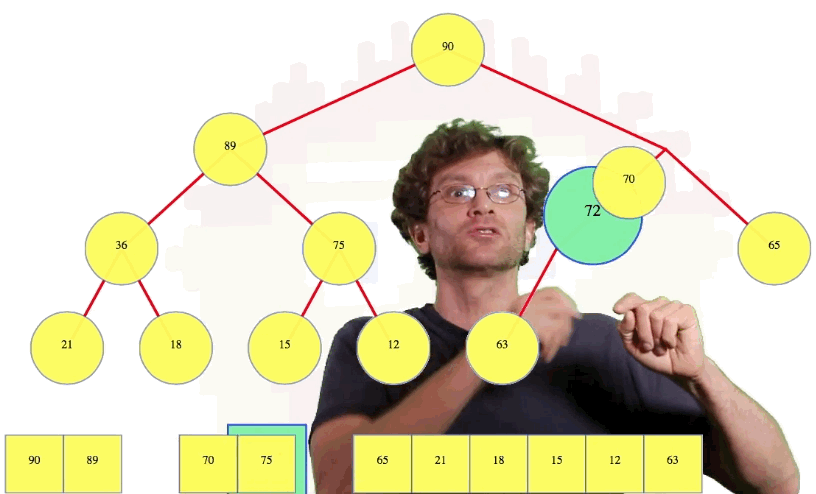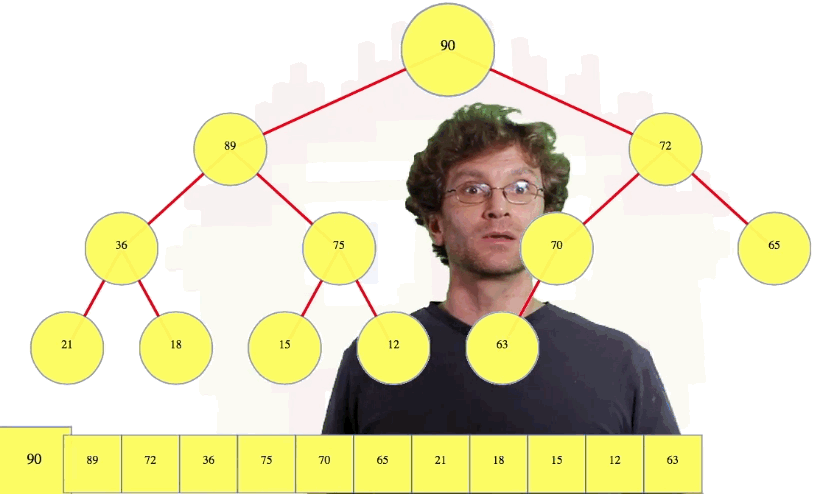
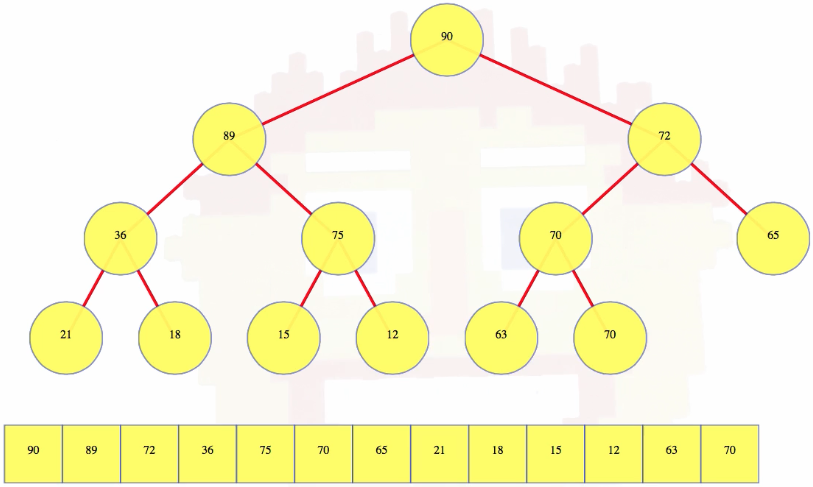
One other thing we can do: let's say we insert a 70 in the tree above. Well, 70 ties with its parent so there's no need to continue swapping nodes. Done. That's insertion and "bubble up".

Deletion and heapify

• Brassard and Bratley: delete-max, sift-down
• Cormen, Leiserson, Rivest, and Stein (CLRS): HEAP-EXTRACT-MAX, MAX-HEAPIFY
• Dasgupta, Papadimitriou, and Vazirani (DPV): deletemin (minheap), siftdown
• Kleinberg and Tardos: ExtractMin (minheap), Heapify-down
• Sedgewick: remove, downheap

How about deletion? Let's pick up where we left off with our tree:

Well, if we want to delete the last leaf, then we can just get rid of it, and there's nothing else to do. But that's a really weird operation because there's nothing special about the last leaf. Basically, it's really easy to delete the last leaft, but there's not much of a reason to do it.

Much more likely, we want to delete the root. The root is a special value. This is a max-heap so the root is the maximum value. So we're going to take that root, and we are going to swap it with the last leaf, and then we're going to delete the last leaf, which we know is very easy to do. Things look pretty good at this point:

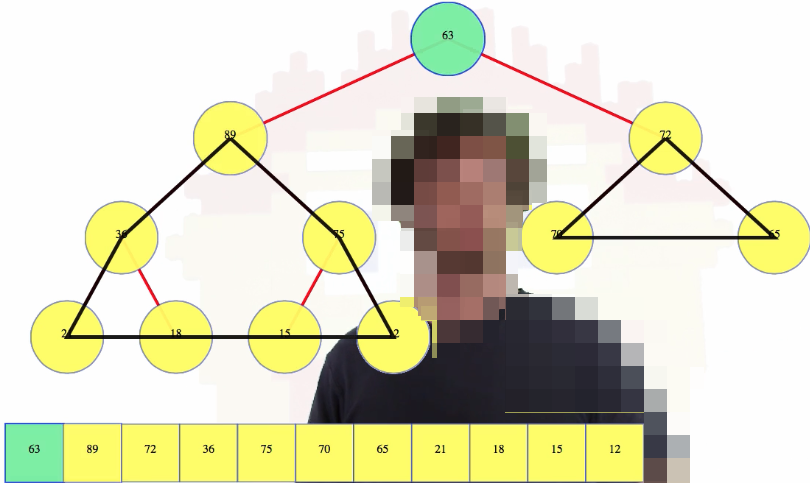
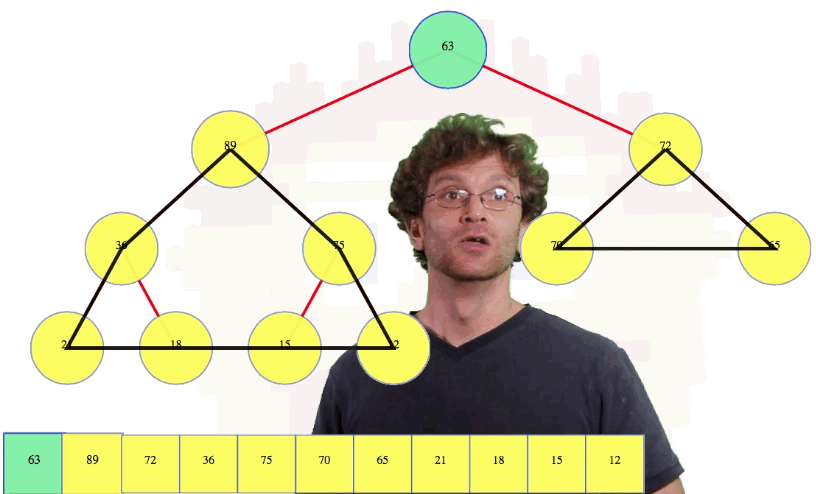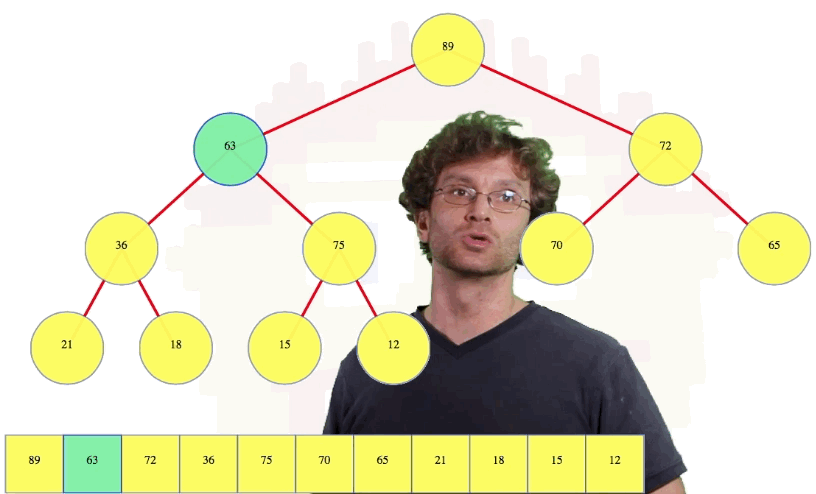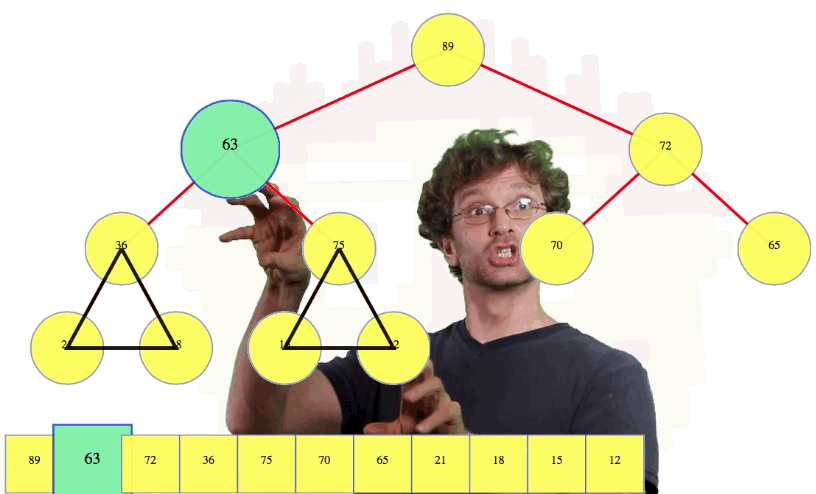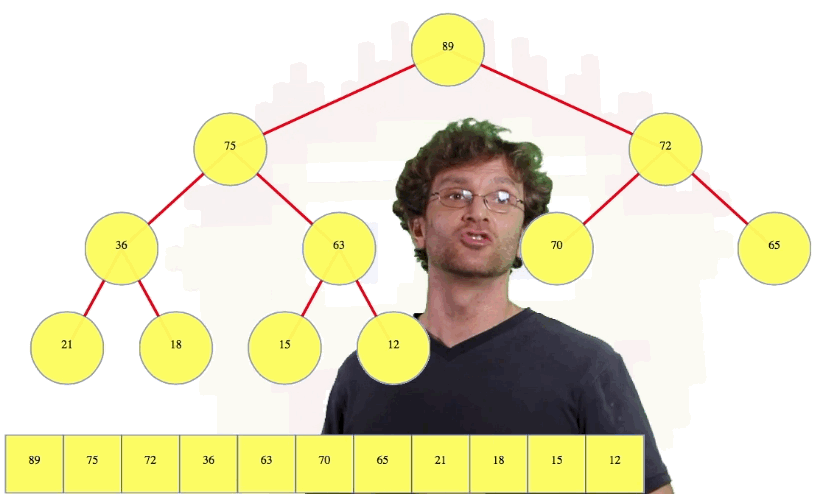
We have the two subheaps pictured above, and the 63, which was the last leaf, is now at the root (which might not have the right value). This operation is often called max-heapify (or other names in different sources). This is probably the most critical operation for a heap. We have two perfect heaps, and a node above them now that gives the correct overall heap shape, but this root node may have a value that violates our important second property: the heap property. That is, the root node's new value after a deletion might have a value which is not larger than the value of its children (one or both), which is the case above.

In the case above, we compare the new root value, 63, with its left child, 89. Since the left child is bigger, we're going to compare the left child to the right child (i.e., 89 compared to 72) because we want to know which child is larger, the left child or the right child. Since the left child is larger, we're going to swap the root with its left child in this case. Then we're going to compare our node again to its left child, 36. The node itself is bigger so we're going to compare our node to its right child, 75. The right child is bigger so we're going to swap them. Now we compare the node to its left child, 15, and its right child, 12, and since it's bigger than both, we stop:

Let's see one more deletion example:

Efficiency

The following concisely summarizes the worst-case efficiency of heaps:

• $O(1)$ find max
• $O(\lg n)$ insert
• $O(\lg n)$ delete

Finding the max value is very easy. This is, in large part, the main purpose of this data structure. Finding the max value can be done in constant time.

For insertion, assuming we have enough room at the end of our array to just put a value there in constant time, well, for each level of the tree we might have to do one comparison and one swap, up to the height of the tree. That's logarithmic time.

For deletion, we start off with a swap; then, for each level that a node might go down, we're going to have two comparisons maybe, and one swap, again logarithmic in time.

Hence, we have the following for insertion and deletion:

• The height of the heap, for $n$ nodes, is $\Theta(\lg n)$.
• Insertion: each level new value moves up takes $\Theta(1)$ time. $\Theta(\lg n)$ (worst-case) time.
• Delete Max: displaced leaf moves up (like insertion) or down (not both). Each level $\Theta(1)$ time. $\Theta(\lg n)$ (worst-case) time.

Linear time BuildHeap

Iterated insertion

What about just inserting whatever values we want? We can build a heap by iterated insertion, which looks great at first, because the heap is small, and insertion is quick. But as the heap gets bigger, elements are inserted deeper down. In the worst case, we insert elements in increasing order, and it will take $n\lg n$ time. The last half of the elements inserted are all at about $\lg n$ depth, and each might need to bubble all the way up to the root.

Iterated insertion analysis

To be fair, iterated insertion gets a bit of a bum rap: for a set of values in random order, most don't really bubble up too much. Most values end up near the bottom of the tree, and each insertion will, on average, take just a couple of swaps (but that analysis is definitely not basic).

To recap, for $n$ insertions:

• Worst-case runtime: $\Theta(n\lg n)$
• Expected over random permutations: $\Theta(n)$

buildHeap operation

• Brassard and Bratley: make-heap
• Cormen, Leiserson, Rivest, and Stein (CLRS): BUILD-MAX-HEAP
• Dasgupta, Papadimitriou, and Vazirani (DPV): makeheap
• Goodrich and Tomassia: BottomUpHeap

There is a worst-case linear time buildHeap operation. It uses the same observation as in iterated insertion: most nodes have a small height (this is necessarily the case for a complete binary tree, where the nodes on the last level(s) dominate). It works bottom-up. For our heap definition, we know that every node in a heap will root a valid sub-heap. Now, no matter what values someone gives us, any single node with no children looks like a valid heap.

Taking whatever value is given to us, the values that fall into the leaf positions look good on their own. Half of the nodes are leaf nodes, so that's not a big deal. Going from the last node, towards the first, we eventually get to a node that is the parent of some other node:

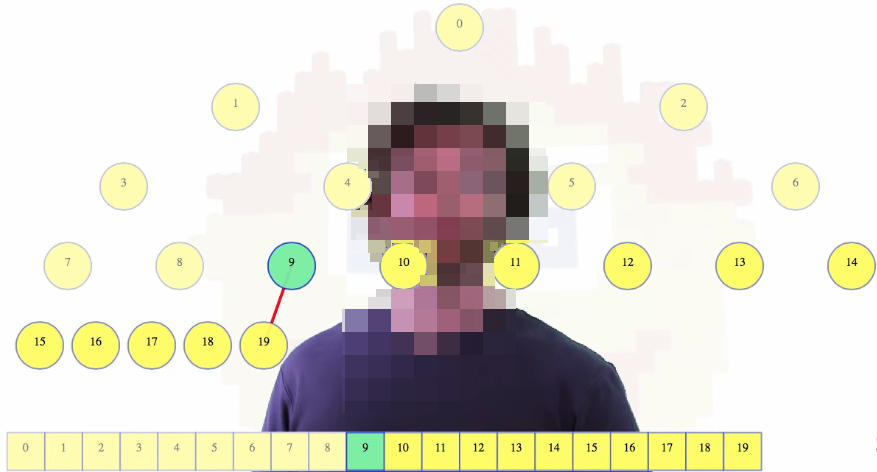
Above, we can imagine starting at 19, then going to 18, then 17, 16, ... , until we get to 9, which is a parent of some other node, namely 19. Considering node 9 as the root of a sub-heap, it still has the shape of a heap, but its value violates the heap property (i.e., its value isn't bigger than the value in each of its children). But this is exactly the place where our max-heapify operation can be used to fix the heap. So use it.

For the next $n/4$ nodes, we will do the same thing: we will use max-heapify to fix all of the small heaps of height 1. Continuing, we fix the $n/8$ heaps of height 2, the $n/16$ heaps of height 3, and so on.

The one case that was easiest for the iterated insertion is now the node that looks worst, the root. But for the $n/2$ nodes that were worst for the iterated insertion, they are now trivial, because they are already heaps to begin with.

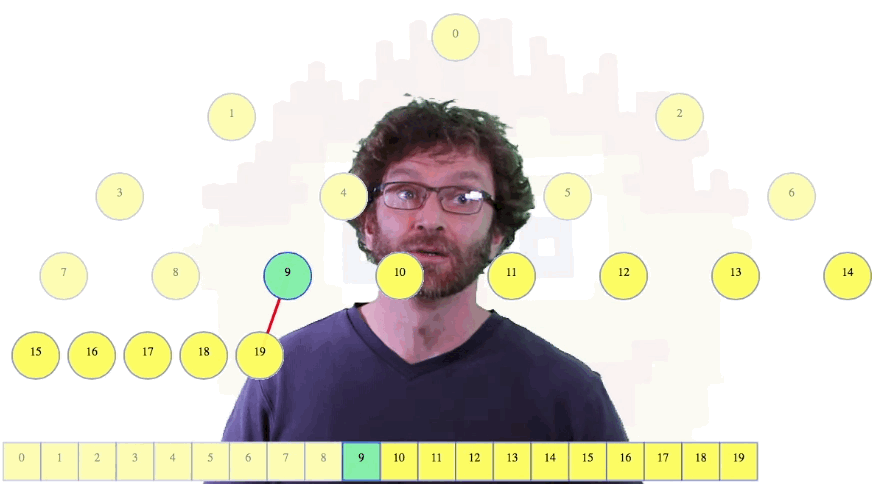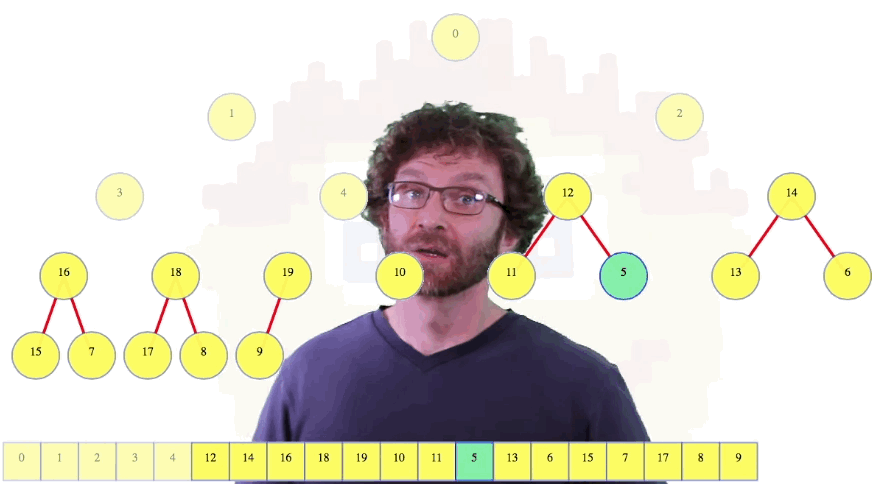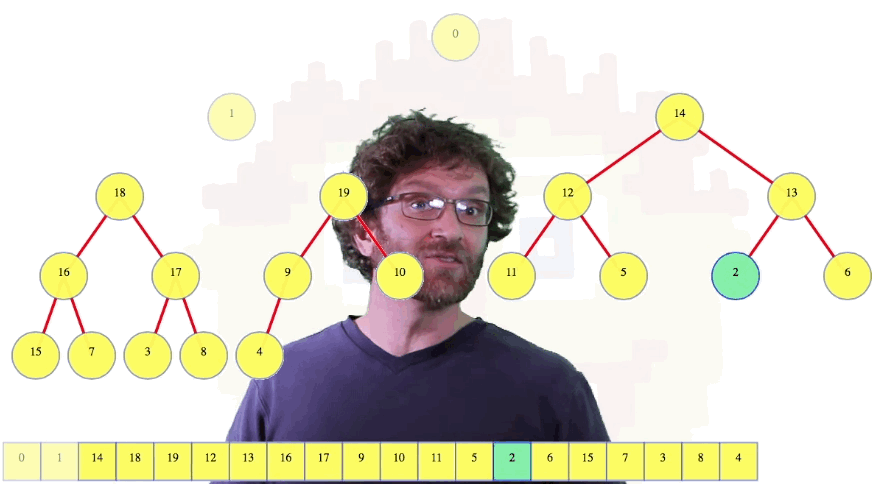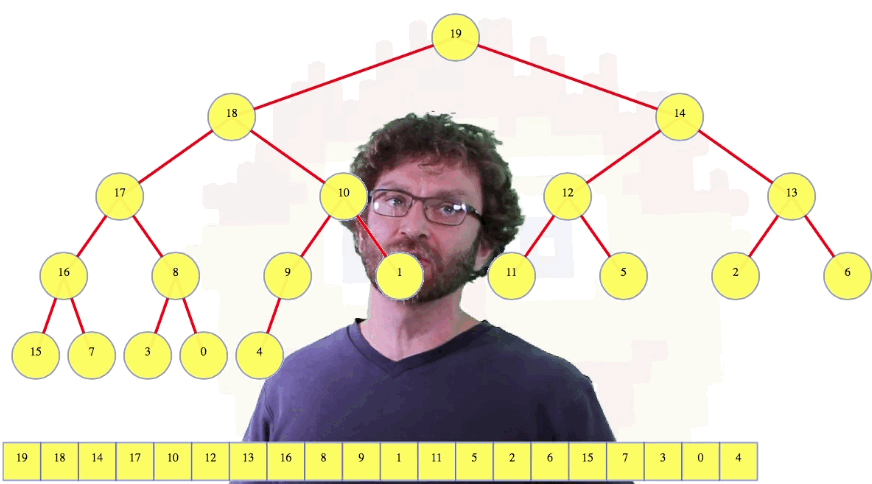
For our worst-case analysis, we are now dealing with the sum of node heights in the final heap rather than the sum of node depths. Fewer nodes have a larger height. Note that these two methods might not give the same heap. In fact, given a random starting permutation, they won't end up even having the same probability distribution over different heaps.

Informal analysis

For each heapify operation, the worst-case runtime is proportional to the starting height of that node. We start off with at least half the nodes being at height 0 and can be skipped altogether (each node constitutes a trival max sub-heap):

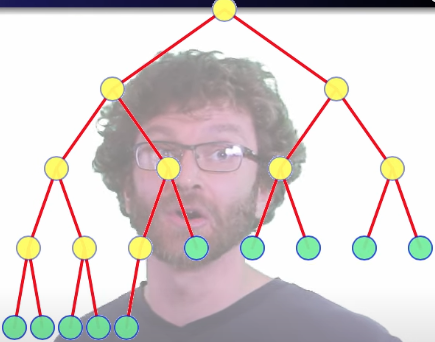
A quarter of the nodes move down one level:

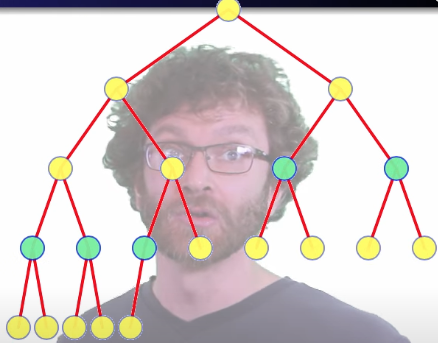
An eighth move down two levels:

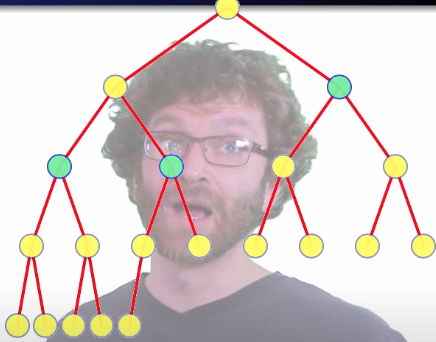
We can generalize the number of nodes at any given height:

• $\sim n/2$ nodes height $0$
• $\sim n/4$ nodes height $1$
• $\sim n/8$ nodes height $2$
• $\sim n/2^{i+1}$ nodes height $i$

And sum over all node heights: $O(\sum_{h=0}^{\lfloor \lg n \rfloor} h\cdot\frac{n}{2^{h + 1}})$. With a bit of manipulation (i.e., calculus), this gives us order $n$ worst-case runtime:

$$\sum_{h=0}^{\lfloor \lg n \rfloor} h\cdot\frac{n}{2^{h + 1}}\leq\sum_{h=0}^\infty h\cdot\frac{n}{2^{h + 1}} < n$$

Exercise

If we want to make this more formal, but also simplify the math, then we should first prove something about the structure of the heap. In a heap of $n$ values, there are $\lfloor n/2^i \rfloor$ nodes of height $i$ or greater:

Prove: $\lfloor n/2^h \rfloor$ nodes height $\geq h$.

This can be proved with induction.

Clever analysis

When being heapified, only the values that start at height at least 1 can be moved down even one level:

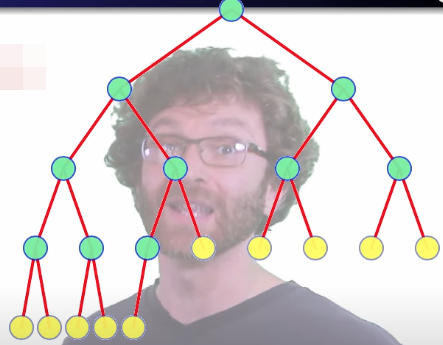
In the worst case, all of those nodes do move down one level. Nodes starting at height 2 (or higher) can each move down a second level:

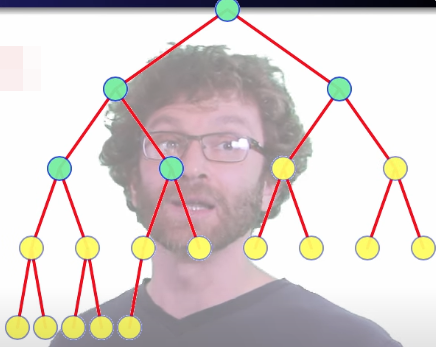
But we have already moved them down one level, so we only have to count one extra to move down that second level. Nodes starting at height 3 (or higher) can move down a third level.

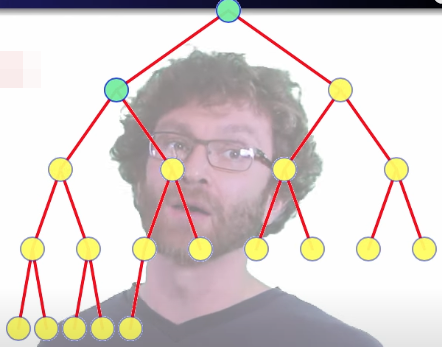
Previously, we saw that we needed to prove that $\lfloor n/2^h \rfloor$ nodes have height $\geq h$, and we just observed the following:

• For $\lfloor n/2 \rfloor$ nodes height $\geq 1$, move down one level each.
• For $\lfloor n/4 \rfloor$ nodes height $\geq 2$, move down a second level each.
• For $\lfloor n/8 \rfloor$ nodes height $\geq 3$, move down a third level each.
• For $\lfloor n/2^h \rfloor$ nodes height $\geq h$, move down an $h$th level each.

This gives us a summation that is easier to bound than the original summation (and a simple proof of the linear runtime):

$$\sum_{h = 1}^{\lg n}\lfloor n/2^h\rfloor \leq n\sum_{h=1}^\infty 2^h = n\cdot(1/2 + 1/4 + 1/8 + \cdots) = n$$

Heap sort

Overview

Suppose we have the heapify and deleteMax operations as well as the buildHeap operation. Heap sort is then quite easy: first, build a max-heap; then, delete all its values:

• buildHeap()
• deleteMax() $n$ times

Done.

buildHeap() phase

For a bit more detail, we start with the buildHeap operation. We assume we're given an array of values to be sorted, and we use the space of that array to store the heap itself. One of the nice properties of heap sort is that it is an in-place algorithm — it only needs a fixed amount of memory beyond what is used to store the data being sorted.

deleteMax() phase

Next, we delete the max value. We swap the root with the last leaf node (bottom level to the far right) and then delete the last leaf node — the new root value then has to be compared to its children and possibly sifted down the tree to ensure the properties of the whole heap and all sub-heaps are respected. We conclude the sifting down when what was previously the last leaf node is now either a leaf or the root of its own sub-heap.

We continue to call deleteMax until the entire array is empty. As indicated above, note that when deleteMax is called, we don't just overwrite the value to be deleted — we swap it with the last leaf of the heap, and continue as explained above. What happens is that we delete more and more items, and the heap gets smaller and smaller. But all of the values are still stored in the array, until finally, the heap is gone.

Analysis

• buildHeap: $O(n)$
• deleteMax $n$ times: $O(\lg n)$ each, $O(n\lg n)$ total

For our analysis, we had a buildHeap operation, which was $O(n)$ time, and then $n$ deleteMax operations, which are worst-case $O(\lg n)$ time each. That's $O(n\lg n)$ total time.

Note that we would still have an $O(n\lg n)$ algorithm even if we ran $n$ insertions to start the algorithm instead of the linear buildHeap. If we want to be more precise, we can better bound the total number of comparisons:

• buildHeap: $< 2n$ comparisons (CLRS)
• delteMax $n$ times: $< 2n\lg n$ comparisons (CLRS)

Note that the above are not asymptotic results. The 2 term above comes from the fact that to move down one level in heapify usually takes 2 comparisons, but that can be improved by optimizing the heapify method, which we'll talk about at the end.

In all, heap sort gives us a worst-case $O(n\lg n)$ in-place sorting algorithm that is not stable. It's supposedly slower in practice than a good quicksort.

Binary heaps for priority queues

We're now going to consider adding a few operations to binary heaps in order to make them more useful for priority queues.

maxHeap vs. minHeap

Thus far, we have mostly been discussing max heaps, but, of course, we could just as well make a min heap instead (e.g., this is the case in Python). It's also worth noting that even though most pedagogical resources just show key values in heaps, heaps can be used to store complex obkects, but those objects will have key values.

Objects vs. references

In the underlying structure, we might have either an array of the complex objects, or an array of object references, where we just swap references within our heap. Details of our heap implementation may change based on which of these two we choose (i.e., storing keys vs. records vs. references), but the abstract heap ideas don't change.

Priority queues

In a heap sort, recall that we built and used a heap a bunch of times, not doing anything else, until we were done with it. But, like most other data structures, we could build a heap, insert some more stuff into it, get the max, delete the max, insert some more stuff into it, and generally use it however we need it over time; that is, it's a very useful data structure to use in real time.

Everything described above also makes heaps a nice data structure for implementing priority queues, where we expect that we have a list of, say, jobs to do: new jobs can arrive at any moment, and, as resources become free, we might choose to do the job of highest priority that's waiting.

Operations

We already have the basic operations needed for this: insert, findMax, and deleteMax. These are all nice, natural looking operations. But what about other operations?

changeKey and delete would be nice:

• changeKey: change the priority of an item in the queue
• delete: delete a given item from the queue (not necessarily the max item for a max heap or a min item for a min heap)

These still seem like pretty basic operations.

changeKey

For changeKey(index, newKey) with heapify/bubble, it's similar to the following in different sources:

• Brassard and Bratley: alter-heap
• Cormen, Leiserson, Rivest, and Stein (CLRS): HEAP-INCREASE-KEY
• Dasgupta, Papadimitriou, and Vazirani (DPV): decreasekey (minheap)
• Goodrich and Tamassia: replaceKey or replaceValue
• Kleinberg and Tardos: ChangeKey
• Sedgewick: change

For changeKey, we're going to jump to the correct index, and if the key decreases, then the node might move down in the heap (like our heapify operation). Or, if the value increases, then we might have to let the node bubble up through the heap, like we did for insertion.

delete

The delete(index) operation is similar to the following operation in different sources:

• Goodrich and Tamassia: remove
• Sedgewick: delete

To delete an arbitrary node, instead of just the max node, we go to that node (by index), exchange it with the last leaf node, and then it might either move up or move down, depending on if the last leaf had a bigger or smaller key than the node being deleted.

The catch

The changeKey and delete operations both probably look somewhat easy, but in both cases they're sort of unnatural: both operations need the index of the node being changed or deleted (this is why a queue augmented with these additional operations is often explicitly called an indexed priority queue instead of just a priority queue). Or, if we're using an explicit heap representation, instead of the implicit array one, then we would need a reference to the node itself. That's kind of a black box no-no. Generally, we shouldn't have to know a reference in order to change an object's key or to delete it.

Here, suppose we have a bunch of jobs, of varying priorities. Maybe we end up adding a field in the job for it to keep track of its heap index. And then the heap code would have to update the index in the job when the job moves around. And now our job code and heap code are kind of dependent on each other. Why would a job have a field for the heap index (or heap node reference)? The job having a priority seems natural, but not for the job to know its heap location. That would mean the writer of the job code needs to know that the job will be stored in a binary heap sometimes and thus make room for that information even though some other priority queue implementations might not need that field.

Options

Our abstraction is kind of hosed here. If we want to change the priority of a job without knowing its index, then a heap doesn't give us any efficient way to find that job. We could use a linear search, but we want these operations to be efficient. In the worst case, we want these operations to take time proportional to the height of the heap (i.e., binary tree), which is logarithmic in the size of the heap. Following a linear search a logarithmic "rest-of-the-operation" doesn't make that operation efficient. It kills our efficiency.

So we have a choice. We could use something other than a binary heap for our priority queue, we could go without the changeKey or delete operations, we could have the changeKey and delete operations but have them be super sow, or we can break our heap black box abstraction.

One last note: if we're using a heap for a priority queue, then we don't have any guarantees about the order that elements will come out if the elements have equal priority. There won't be any "first-in-first-out" guarantees or anything like that. So the simplicity of a heap is great, but it only sort of gives us its natural operations — unless we want to break the abstraction (e.g., indexed priority queue).

Optimized heapify

This is mostly a collection of academic references on different ways to optimize heapify, heap sort, etc. David even mentions this video is not nearly as important as the others in the playlist:

This is, by far, the least important video in the heap series.

The referenced dissertation David suggests as a starting point for those really interested in analyzing heaps more closely: The Analsysis of Heapsort by Russel Schaffer and Robert Sedgewick.

---