Iterative DFS with stack-based graph traversal
Depth-first search (DFS) on a graph (binary tree or otherwise) is most often implemented recursively, but there are occasions where it may be desirable to consider an iterative approach instead. Such as when we may be worried about overflowing the call stack. In such cases it makes sense to rely on implementing DFS with our own stack instead of relying on our program's implicit call stack. But doing so can lead to some problems if we are not careful.
Specifically, as noted in another blog post, it is easy to fall into the trap of using a stack haphazardly and conducting a graph search that is not truly DFS. The issue may go undetected in some problems, but algorithms that rely on a true DFS may fail (e.g., Kosaraju's and Tarjan's algorithms for finding strongly connected components). The linked blog post above is very effective at pointing out the potential issues, but it's quite terse in its treatment. Thus, the linked blog post has been reproduced below for ease of reference (unaltered).
This blog post is primarily intended to further explore the reproduced blog post below (with working Python code).
Illustrating the issue
TLDR
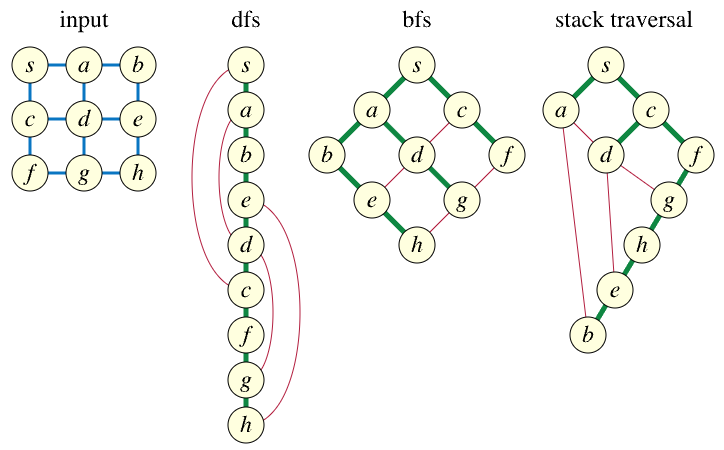
Look at the graph below. If we start a DFS at vertex S, then we may visit either of the following vertices next: A or C. If we visit A from S, then our DFS should naturally lead us to visit either vertex B or vertex D next (we don't go back to vertex S because it's already been visited). If, however, we visit vertex C, then our DFS should naturally lead us to visit either vertex D or vertex F next.
This is not what happens in the (flawed) stack-based traversal. Instead, from vertex S, we end up visiting vertex A and then vertex C, which is not a valid DFS.
Consider the following graph:
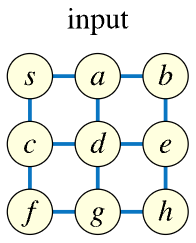
We can represent this graph in code as an adjacency list of index arrays, where vertex S maps to index 0 and vertices A, B, C, ... map to indices 1, 2, 3, ... , respectively (we'll use uppercase notation for the vertices throughout this post despite the figures depicting the vertices in lowercase):
lookup = {
0: 'S',
1: 'A',
2: 'B',
3: 'C',
4: 'D',
5: 'E',
6: 'F',
7: 'G',
8: 'H',
}
graph = [ # Edges:
[1, 3], # S: (S, A), (S, C)
[0, 2, 4], # A: (A, S), (A, B), (A, D)
[1, 5], # B: (B, A), (B, E)
[0, 4, 6], # C: (C, S), (C, D), (C, F)
[1, 3, 5, 7], # D: (D, A), (D, C), (D, E), (D, G)
[2, 4, 8], # E: (E, B), (E, D), (E, H)
[3, 7], # F: (F, C), (F, G)
[4, 6, 8], # G: (G, D), (G, F), (G, H)
[5, 7], # H: (H, E), (H, G)
]
Suppose we wanted to explore the graph above, starting at vertex S as the source. In what order would the other vertices be visited if we conducted a standard BFS and a standard DFS? We would get something like the following (note that the graph above is defined in such a way that neighboring vertices are visited in alphabetical order):
def bfs(graph, source):
n = len(graph)
queue = deque([source])
visited = [False] * n
visited[source] = True
while queue:
node = queue.popleft()
for nbr in graph[node]:
if not visited[nbr]:
visited[nbr] = True
queue.append(nbr)
bfs(graph, 0) # (S) A C B D F E G H
def dfs(graph, source):
n = len(graph)
visited = [False] * n
def visit(node):
visited[node] = True
for nbr in graph[node]:
if not visited[nbr]:
visit(nbr)
visit(source)
dfs(graph, 0) # S A B E D C F G H
Let's now try to implement an iterative DFS with a stack by swapping the queue for a stack in the standard BFS:
def bfs(graph, source):
n = len(graph)
queue = deque([source])
visited = [False] * n
visited[source] = True
while queue:
node = queue.popleft()
for nbr in graph[node]:
if not visited[nbr]:
visited[nbr] = True
queue.append(nbr)
bfs(graph, 0) # (S) A C B D F E G H
def dfs_stack(graph, source):
n = len(graph)
stack = [source]
visited = [False] * n
visited[source] = True
while stack:
node = stack.pop()
for nbr in graph[node]:
if not visited[nbr]:
visited[nbr] = True
stack.append(nbr)
dfs_stack(graph, 0) # (S) A C D F G H E B
Notes on code blocks above:
- Visit order: If we insert the
printstatementprint(lookup[nbr])on line11in standard BFS, line6in standard DFS, and line11in attempted iterative DFS, then we will get the output for each code block referenced as a comment on line14when the defined function is called. - Output notation: The notation
(S)meansSwas already visited and would not be printed with theprintstatement referenced above. The only timeSis not printed is with standard DFS where vertices are marked as visited upon entry into thevisitfunction.
We can gain even more insight from the code blocks above if we add the following print statement whenever a subsequent vertex is discovered:
print(f'Vertex {lookup[nbr]} discovered by {lookup[node]}')
This line allows us to effectively observe from which vertex each subsequent vertex is discovered. We can insert this print statement on line 11 in standard BFS, line 9 in standard DFS, and line 11 in attempted iterative DFS. The output in each case is the following:
Vertex A discovered by S
Vertex C discovered by S
Vertex B discovered by A
Vertex D discovered by A
Vertex F discovered by C
Vertex E discovered by B
Vertex G discovered by D
Vertex H discovered by E
Vertex A discovered by S
Vertex B discovered by A
Vertex E discovered by B
Vertex D discovered by E
Vertex C discovered by D
Vertex F discovered by C
Vertex G discovered by F
Vertex H discovered by G
Vertex A discovered by S
Vertex C discovered by S
Vertex D discovered by C
Vertex F discovered by C
Vertex G discovered by F
Vertex H discovered by G
Vertex E discovered by H
Vertex B discovered by E
The issue becomes more readily apparent if we draw the different search trees whose edges, shown in green, link each vertex with the earlier vertex it was discovered from (the red edges indicate non-discovery or "non-tree" edges, edges that exist in the original graph but were not used when discovering subsequent vertices in the search):
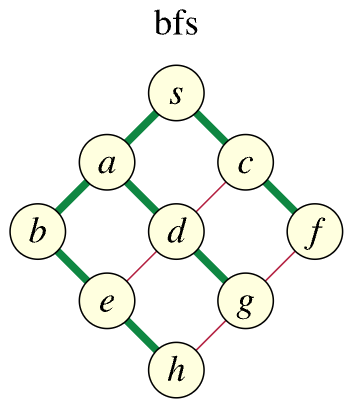
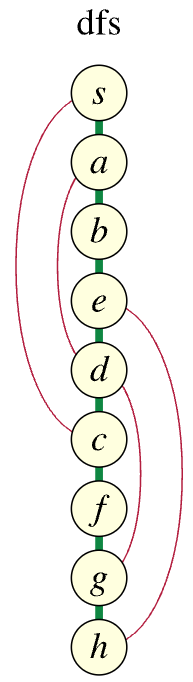
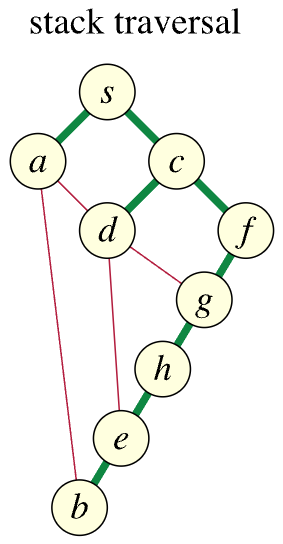
The linked blog post highlights what the issue is with the stack traversal shown above:
The problem is that nodes high in the tree push some of their neighbors as children too early; in a proper depth first search those children would instead be discovered as descendants farther down in the tree.
Recall the input graph we started with:

When conducting a DFS starting at vertex S, what options do we have in regards to what vertex we visit next?
- Vertex
A: Suppose we visit vertexAfirst. Then the next possible vertices to visit in our search should be eitherBorD(we do not want to revisitS). - Vertex
C: Suppose we visit vertexCfirst. Then the next possible vertices to visit in our search should be eitherDorF(we do not want to revisitS).
In either case, it cannot make sense to visit A and C as the next vertices in our search.
But this is precisely what happens in the stack traversal, as illustrated above. Specifically, using the language of the linked post, for the vertex highest in the tree (i.e., S, the search tree root vertex), we push some of its neighbors as children too early (whichever vertex was not chosen first in this case). In a proper DFS, such as the one illustrated in the middle figure above, the children should instead be discovered as a descendant farther down in the tree — when A is chosen, we see that C is discovered as a descendant farther down in the tree.
Finally, let's examine one more excerpt from the linked post:
In a depth first search tree, all edges connect ancestors and descendants. In a breadth-first search tree, all edges connect vertices in the same or adjacent levels. But in the stack traversal tree, all non-tree edges connect pairs of vertices that are not ancestors and descendants of each other, the opposite property to the depth first tree property. Or, to put it another way, if is a descendant of , and is adjacent to , then must be a direct child of .
What does this mean? It helps if we first recall that if we initiate a DFS from some vertex X, then this means we will end up creating a DFS tree with X as its root. For the example we've been considering, this means vertex S is the root of our DFS tree. The middle figure above for the proper DFS shows how every vertex is a descendant of S; specifically, the non-tree edges highlighted in red, namely (S, C), (A, D), (E, H), (D, G), show that S is an ancestor of C, A is an ancestor of D, E is an ancestor of H, and D is an ancestor of G. These are necessary conditions for the tree to be considered a valid DFS tree:
In a depth first search tree, all edges connect ancestors and descendants.
But this isn't the case with the stack traversal tree. The only ancestor of A is S. The only ancestors of D are C and S. But the non-tree edges (A, B), (A, D), (D, G), (D, E) cause problems because the endpoints are neither ancestors nor descendants of each other. Each endpoint lies on a different branch. The stack traversal tree is not a depth first tree.
Fixing the issue
The blog post mentions two ways of fixing the issue. The first way is to use a stack of iterators instead of a stack of vertices:
def dfs_stack_iterators(graph, source):
n = len(graph)
visited = [False] * n
visited[source] = True
stack = [iter(graph[source])]
while stack:
try:
node = next(stack[-1])
if not visited[node]:
visited[node] = True
stack.append(iter(graph[node]))
except StopIteration:
stack.pop()
This approach is space-efficient in its use of iterators, essentially allowing the iterative method to pause and resume the exploration of a vertex's neighbors (i.e., similar to the standard recursive approach with function calls). The efficiency lies in how each iterator keeps track of where it left off in the adjacency list, thus avoiding the need to reprocess neighbors. This approach matches the standard recursive DFS in terms of both the order in which vertices are visited and the space requirement as well. But using a stack of iterators is somewhat unusual.
A second way to fix the issue is to still use a stack of vertices but to change up how future vertices are processed. Instead of checking to see if a vertex's neighbors have been visited before adding the neighbors to the stack (i.e., the problematic stack traversal way), we push all neighbors to the stack and delay the check for whether or not a neighboring vertex has been visited until after it is popped from the stack:
def dfs_stack_bad(graph, source):
n = len(graph)
stack = [source]
visited = [False] * n
visited[source] = True
while stack:
node = stack.pop()
for nbr in graph[node]:
if not visited[nbr]:
visited[nbr] = True
stack.append(nbr)
dfs_stack(graph, 0) # (S) A C D F G H E B
def dfs_stack_good(graph, source):
n = len(graph)
visited = [False] * n
stack = [source]
while stack:
node = stack.pop()
if not visited[node]:
visited[node] = True
for nbr in graph[node]:
stack.append(nbr)
dfs_stack_good(graph, 0) # S C F G H E D A B
Note how the check for whether or not a vertex has been visited should happen immediately after the vertex is poppped from the stack (line 9 in the good attempt). The tradeoff for this second approach of using a stack of vertices is that it uses more space because of duplicated entries on the stack. Additionally, this second approach reverses the order of the children at each vertex (if we add items 1, ... , N to a stack, then they will be popped off and processed in reverse: N, ... , 1). If we really want to perform an iterative stack-based DFS that mimics as close as possible the standard recursive DFS approach, then we need to process neighbors in reverse order:
def dfs_iterative(graph, source):
n = len(graph)
visited = [False] * n
stack = [source]
while stack:
node = stack.pop()
if not visited[node]:
visited[node] = True
for i in range(len(graph[node]) - 1, -1, -1):
nbr = graph[node][i]
stack.append(nbr)
As also mentioned in the blog post, both approaches above have the property that replacing the stack by a queue gives a breadth-first search, albeit implemented in a somewhat nonstandard way.
Experimenting with different traversals
The code editors below use Piston API, which has a hard cap of 1024 characters for output (i.e., stdout). There are other limiting security features as well, but the main thing to remember is that if the output exceeds the 1024 character cap, then the output box below the editor will read No output. Hence, for the first subsection below, don't run all functions at once (the output character limit will be exceeded); instead, try running each function individually by uncommenting it.
Blog post traversals
All of the traversals and their variants remarked on above in this post can be difficult to absorb all at once. It can help to see each traversal implemented in one environment, where discovered nodes and the nodes by which they are discovered are detailed explicitly:
Click "Run Code" to see the output here
Your own traversals
Try experimenting with your own traversals by tweaking different approaches in the editor above or by engineering something completely new. The graph definition and corresponding lookup have been pre-filled for ease of use and reference.
Click "Run Code" to see the output here
Stack-based graph traversal ≠ depth first search (original blog post)
The blog post below is a reproduction of David Eppstein's blog post: stack-based graph traversal ≠ depth first search. It has been reproduced below (without changes) for ease of reference.
I just finished teaching our required undergraduate algorithms class, and in grading their final exams I discovered that a few of the students have (not from me) acquired the incorrect belief that modifying the standard version of the breadth first search algorithm by replacing the stack with a queue makes it into depth first search. Embarrassingly, the Wikipedia depth first search article made the same mistake (until today), as do some textbooks (for example Skiena's Algorithm Design Manual p. 169; Jeff Edmonds' How to Think about Algorithms, pp. 175–178; Gilberg and Forouzan Data Structures: A Pseudocode Approach Using C, 2nd ed., p. 497).
Here's what you get if you swap a stack for the queue in breadth first search:
def stack_traversal(G,s):
visited = {s}
stack = [s]
while stack:
v = stack.pop()
for w in G[v]:
if w not in visited:
visited.add(w)
stack.append(w)
In trees, or in AI search contexts where the visited set is not used to eliminate duplicate vertices, this idea does indeed produce a depth-first search. But in arbitrary graphs with a visited set, the traversal that you get from this routine is not depth first. The problem is that nodes high in the tree push some of their neighbors as children too early; in a proper depth first search those children would instead be discovered as descendants farther down in the tree. Here's an example, illustrating (as usual) the tree whose edges link each vertex with the earlier vertex it was discovered from:
In a depth first search tree, all edges connect ancestors and descendants. In a breadth-first search tree, all edges connect vertices in the same or adjacent levels. But in the stack traversal tree, all non-tree edges connect pairs of vertices that are not ancestors and descendants of each other, the opposite property to the depth first tree property. Or, to put it another way, if is a descendant of , and is adjacent to , then must be a direct child of .
Goodrich and Tamassia (whose book I used for my class) and CLRS avoid this mistake by only discussing recursive depth-first search; CLRS has an exercise of writing an iterative stack-based depth-first search but doesn't state the answer. One text that discusses the subject of using a stack for an iterative depth first search but gets it right is Sedgewick's Algorithms in Java. There are (at least) two different ways of doing it, both discussed by Sedgewick. You can use a stack of iterators instead of a stack of vertices:
def dfs(G,s):
visited = {s}
stack = [iter(G[s])]
while stack:
try:
w = stack[-1].next()
if w not in visited:
visited.add(w)
stack.append(iter(G[w]))
except StopIteration:
stack.pop()
Alternatively, you can push all neighbors and delay the check for whether a vertex has been visited until it is popped. This is the approach taken by Kleinberg and Tardos's Algorithm Design:
def dfs2(G,s):
visited = set()
stack = [s]
while stack:
v = stack.pop()
if v not in visited:
visited.add(v)
for w in G[v]:
stack.append(w)
Both of these have the property that replacing the stack by a queue gives a breadth-first search, implemented in a somewhat nonstandard way. They don't give the same traversal as each other (the first one matches the usual recursive dfs while the second one reverses the order of the children at each vertex), and the second one uses more space because of duplicated entries on the stack, but they at least both give a valid depth-first search.
Depth-first search and breadth-first search (and lexicographic breadth-first search) are all useful in algorithm design because of the restricted way the rest of the graph can be attached to the search tree. The non-dfs stack traversal is a different type of graph traversal, so conceivably it could also be useful in this way. But I don't know of any examples of algorithms that deliberately use it instead of bfs or dfs.
