Introduction to monotonic stacks and queues (with LeetCode problems and more)

April 26, 2024

Software Engineer

Monotonic stacks and queues have a reputation for being notoriously difficult. Why? I suspect the difficulty lies not in what these data structures are but how they are often used to craft solutions to various problems.

This post explores monotonic stacks and queues by first exploring the next greater height problem without any framing whatsoever (i.e., there's no mention of explicitly using a monotonic data structure in any capacity). We then try to use one of the approaches developed for solving the next greater height problem to solve another problem: the sliding window minimum. But our previously developed approach is not quite enough. We need to make a small tweak that turns out to be quite insightful (this leads us to monotonic deques or "monotonic double-ended queues").

The approaches developed for solving both problems are used to set the stage for explaining what monotonic stacks and queues are in a technical sense and why we may want to consider using them in service of solving different kinds of problems. General code templates are provided for maintaining monotonically increasing/decreasing stacks and deques. If you are able to follow the solutions for the introductory problems (i.e., next greater height and sliding window minimum), then you will already know the core of what you need to know about monotonic stacks and deques before being explicitly told their definitions.

Several LeetCode problems are provided where monotonic stacks and/or deques serve as natural tools in crafting optimal solutions (several problems are solved using the concepts fleshed out in this post). An "epilogue" is included at the end of this post, where one problem of notable difficulty is thoroughly examined and solved efficiently by creative use of a monotonic stack.

TLDR

Read the important observations section if you don't have time for much else.

Stacks and queues are defined by their interfaces (e.g., push, pop, enqueue, dequeue, peek, etc.). Monotonicity is not. The following are all examples of monotonic stacks, where the removal of values needed to maintain the monotonic invariant (i.e., strictly/weakly increasing/decreasing) is illustrated in the context of adding 5 to each value collection:

Strictly decreasing
[12, 10, 9, 5, 3, 2, 1] # Before addition of 5
[12, 10, 9, 5]          # After addition of 5

Weakly decreasing
[12, 10, 10, 9, 5, 3, 1, 0] # Before addition of 5
[12, 10, 10, 9, 5, 5]       # After addition of 5

Strictly increasing
[0, 1, 3, 5, 6, 10, 11] # Before addition of 5
[0, 1, 3, 5]            # After addition of 5

Weakly increasing
[1, 2, 2, 3, 5, 7, 8, 10] # Before addition of 5
[1, 2, 2, 3, 5, 5]        # After addition of 5

The removals above are all stack-like in nature (i.e., popping and pushing from the right), which is why the term "monotonic queue" can be rather misleading. If elements need to be removed from the left, then we use a double-ended queue or deque (e.g., see Python's deque from its collections module). Stack-like operations (push and pop) are always performed on the right end to maintain the monotonic invariant. If the queue-like operation of removing an element from the left end (dequeue) is needed, then we can use a deque instead of a simple stack (this allows us to still use stack-like operations to maintain the monotonic invariant while also allowing us to pop elements from the left, as needed).

What can make monotonic stacks and deques challenging at first is not what they are (all possibilities are shown above) but how they are used in sophisticated ways to solve problems of varying complexity. This post thoroughly explores two introductory problems and various approaches to solving these problems without ever mentioning the words monotonic, stack, queue, or deque (double-ended queue). The ideas behind these structures are used though, where an emphasis is placed on trying to use these ideas as organically as possible (i.e., not getting mired in technical mumbo jumbo but exploring new ways of thinking). If you can make it through the "next greater height" and "sliding window minimum" introductory problems, then you will largely know what you need to know about monotonic stacks and deques.

Template quick access ("next" and "previous" value templates and illustration of monotonic deque)

Combined templates for finding previous and next values in a single pass
def fn(nums):
    n = len(nums)
    ans = [[-1, -1] for _ in range(n)] # default values for missing PREVIOUS and NEXT values, respectively
    stack = [] # monotonic stack
    
    # the comparison operator (?) dictates what each element's PREVIOUS and NEXT values will be
    # (<=) PREVIOUS larger value and NEXT larger or equal value (strictly decreasing stack)
    # (<)  PREVIOUS larger or equal value and NEXT larger value (weakly decreasing stack)
    # (>=) PREVIOUS smaller value and NEXT smaller or equal value (strictly increasing stack)
    # (>)  PREVIOUS smaller or equal value and NEXT smaller value (weakly increasing stack)
    for i in range(n):
        while stack and nums[stack[-1]] ? nums[i]:
            # NEXT values processed
            idx = stack.pop()
            ans[idx][1] = i # use nums[i] instead of i to directly record array values instead of indexes
        # PREVIOUS values processed
        ans[i][0] = -1 if not stack else stack[-1] # use nums[stack[-1]] instead of stack[-1] 
                                                   # to directly record array values instead of indexes 
        stack.append(i)
    
    return ans

Template for finding A's next value B
def fn(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_B = nums[i]
        # the comparison operator (?) dictates what A's next value B represents
        # (<)  next larger value (weakly decreasing stack)
        # (<=) next larger or equal value (strictly decreasing stack)
        # (>)  next smaller value (weakly increasing stack)
        # (>=) next smaller or equal value (strictly increasing stack)
        while stack and nums[stack[-1]] ? val_B:
            idx_val_A = stack.pop()
            ans[idx_val_A] = val_B
        stack.append(i)
    
    # process elements that never had a "next" value that satisfied the criteria
    while stack:
        idx_val_A = stack.pop()
        ans[idx_val_A] = -1
    
    return ans

Template for finding A's previous value B
def fn(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_A = nums[i]
        # the comparison operator (?) dictates what A's previous value B represents
        # (<)  previous larger or equal value (weakly decreasing stack)
        # (<=) previous larger (strictly decreasing stack)
        # (>)  previous smaller or equal value (weakly increasing stack)
        # (>=) previous smaller value (strictly increasing stack)
        while stack and nums[stack[-1]] ? val_A:
            stack.pop()
            
        if stack:
            idx_val_B = stack[-1]
            val_B = nums[idx_val_B]
            ans[i] = val_B
        else:
            ans[i] = -1
        
        stack.append(i)
        
    return ans

Monotonic deque (weakly decreasing)
from collections import deque
def fn(nums):
    queue = deque() # monotonic deque (weakly decreasing)
    ans = []
    
    for i in range(len(nums)):
        curr_num = nums[i]
        while queue and nums[queue[-1]] < curr_num:
            queue.pop()
        queue.append(i)
        
        if CONDITION:
            queue.popleft()
        
    return ans

Note about monotonic deque

The code in the template above is virtually the same as the code used to maintain a monotonic stack (weakly decreasing) with one notable exception:

def fn(nums):
    dec_stack = []
    ans = []
    
    for i in range(len(nums)):
        curr_num = nums[i]
        while dec_stack and nums[dec_stack[-1]] < curr_num:
            dec_stack.pop()
        dec_stack.append(i)




    return ans

The highlighted block above with nothing in it shows how the code that triggers popping an element from the left based on some CONDITION has been removed. That's generally the only notable difference between code that uses a stack versus that which uses a deque.

Next greater height
Sliding window minimum
Monotonic stacks and queues (deques)
LeetCode practice problems
- Monotonic stacks
- Monotonic queues
Solved practice problems
Epilogue: Sum of subarray minimums and subarray ranges

Next greater height

Perhaps the best way to start our exploration of monotonic stacks/queues is by considering a problem with no framing (i.e., we'll worry about what monotonic stacks/queues actually are at a later point). This video introduces monotonic stacks with the problem of finding the next greater height value (left to right) for a row of people lined up (or -1 if a next greater height does not exist):

The heights, heights = [12, 11, 12, 14, 13], are listed above each person in magenta, and the final reported answer is the cyan box on the bottom: ans = [14, 12, 14, -1, -1]; that is, the next greater height for the first person of height 12 is the fourth person of height 14, and the next greater height for the second person of height 11 is the third person of height 12, and so on. Let's go through some solution approaches for obtaining these answers.

Approach 0 (brute force)

How would you solve this problem if you were out in the wild (i.e., if you really had a row of people in front of you with their heights labeled above them)? You would probably do what I would do along with most other people:

Start with the first (leftmost) person. Then move left to right across the row (beginning at the second person) until you've identified a person with a height greater than the first person. Record that height (or -1 if the search was unsuccessful).
Start with the next (second) person. Move left to right across the row (beginning at the third person) until you've identified a person with a height greater than the second person. Record that height (or -1 if the search was unsuccessful).
Start with the next (third) person. And so on.

This brute force approach is intuitive and not too difficult to implement with code (we pre-fill the answer array with -1 to avoid having to manually make such assignments after unsuccessful searches):

def next_greater_height_0(heights):
    # pre-fill the answer array with -1
    ans = [-1] * len(heights)

    # start with the leftmost person
    for i in range(len(heights) - 1):
        curr_height = heights[i]

        # begin looking for the next greater height
        for j in range(i + 1, len(heights)):
            next_height = heights[j]

            # if a greater height is found, update the answer array
            if curr_height < next_height:
                ans[i] = next_height
                break

    return ans

What's the computational burden of the approach above (i.e., what is the time and space complexity of the next_greater_height_0 function)?

Time: If heights has $n$ elements, then how many total iterations can we possibly perform? The worst-case scenario is if the heights input array is strictly decreasing (because then no height will have a next greater height and we must exhaust the search space every time we look for a next greater height). Our function appears to be $O(n^2)$ in terms of time complexity, but let's confirm this — the inner loop is where the heavy lifting is done. How many times can we possibly enter the innermost loop and perform an operation in the worst-case scenario? The table below shows how many times the innermost loop can fire (i.e., how many elements are traversed or "people searched" in service of looking for a next greater height for index i):
$\begin{array}{l|cccccc} i\ \text{index} & 0 & 1 & 2 & \cdots & n-3 & n-2\\\hline j\ \text{iterations} & n-1 & n-2 & n-3 & \cdots & 2 & 1 \end{array}$
We can have a total of $(n-1) + (n-2) + \cdots + 2 + 1$ iterations. This is the sum of the first $n-1$ positive integers. Since the sum of the first $n$ positive integers is given by the formula $n(n+1)/2$ , we can see that our sum amounts to $(n-1)((n-1) + 1) / 2 = n(n-1)/2 = O(n^2)$ , as expected. Hence, the brute force approach above is $O(n^2)$ in terms of time complexity.
Space: For space complexity, no additional memory is consumed as the size of the input array heights scales to infinity; hence, the space complexity is $O(1)$ .

There's nothing wrong with the approach above. But a time complexity of $O(n^2)$ is often not considered to be that great unless it's completely unavoidable. Is this completely unavoidable when trying to solve this problem?

Approach 1 (right to left, single pass)

Is there a way to improve on the $O(n^2)$ time complexity for the brute force solution above? Is it possible for us to compromise on space to get a solution that is $O(n)$ time and $O(n)$ space (e.g., the same compromise is made for the intended solution to LC 1. Two Sum), where we maintain some sort of data structure to help us figure out each person's next greater height? Maybe. Let's see if we can figure this example problem out manually/verbally first before coding anything up.

Process description

If we started processing the height of each person from the right, then maybe we could use the heights we've seen thus far to determine the next greater height for each element as we proceed from right to left. Here's one possible way we could do this (the people-indexing is 0-based), first recalling the heights of the people to be processed, heights = [12, 11, 12, 14, 13]:

Person	Height	Process Description
`4`	`13`	This is the rightmost person so there cannot be another person to the right with a greater height. We report `-1` for this person since there is no next greater height, and we store the height we've just seen so we can reference it later, if needed: `[13]`.
`3`	`14`	What heights have we seen thus far? We have `[13]` and that's it. But that's not greater than `14`. So we report `-1` for this person too. How should we store the height of `14` we've just encountered so that we can effectively reference it later, if needed? Should we still keep the `13` in the collection of heights we've seen so far: `[13]`? No, because any height that could have `13` as its next greater height would certainly have `14` as its actual next greater height since `14` comes before `13` in the left-to-right row of people. It does not benefit us at all to keep the `13` so we remove it. Then we add `14`: `[14]`.
`2`	`12`	Do we have a height greater than `12` that we can reference that might be a candidate for its next greater height? Yes! We can finally use our small collection `[14]` effectively. The height of `14` is the next greater height. So we report `14` for this person. What should we do with the height of `12` we just saw? Should we add it to our collection or not? If we didn't add it to our collection, then we could potentially see a height in the near future that is smaller than `12`, say `1`, and reporting `14` as the next greater height would be inaccurate (because `12` would actually be the next greater height). So we should add `12` to the collection: `[14, 12]`.
`1`	`11`	Do we have a height greater than `11` that we can reference that might be a candidate for its next greater height? Yes! Our collection right now is `[14, 12]`, but the `14` comes after the `12` in terms of the order in which these heights are encountered; hence, we will report `12` for this person. What should we do with the height of `11`? For the same reasons as noted above, we should add `11` to our collection: `[14, 12, 11]`.
`0`	`12`	Do we have a height greater than `12` that we can reference that might be a candidate for its next greater height? Yes! Our collection right now is `[14, 12, 11]`. How does this help? Because of how we've arranged the collection (from biggest height to smallest and in the order we've encountered them). This means we first test `11` as a candidate. It's not greater than `12` so we remove it from our collection: `[14, 12]`. What about `12`? It is also not greater than `12` so we remove it from our collection too: `[14]`. What about `14`? It is greater than `12` so we will report `14` as the next greater height for this person. We now add `12` to our collection and continue to process heights as we've been doing. But we're now at the end of the row of people we're considering for this specific example; hence, the state of our final collection we've been maintaining is as follows: `[14, 12]`.

It may be illustrative to show a condensed table where the reported next greater height for each person is included as well as what our height reference collection looks like after processing each person:

Person	Height	Next greater height	Height collection after person processed
`4`	`13`	`-1`	`[13]`
`3`	`14`	`-1`	`[14]`
`2`	`12`	`14`	`[14, 12]`
`1`	`11`	`12`	`[14, 12, 11]`
`0`	`12`	`14`	`[14, 12]`

Code implementation

Now for the code implementation of the process described above:

def next_greater_height_1(heights):
    height_collection = []
    ans = [None] * len(heights)
    for i in range(len(heights) - 1, -1, -1):
        curr_height = heights[i]

        # remove all height collection references less than or equal to the current height
        while height_collection and height_collection[-1] <= curr_height:
            height_collection.pop()
        
        # if collection of height references is empty, then there's no next greater height: -1
        if not height_collection:
            ans[i] = -1

        # if height collection is non-empty, then next greater height must be the
        # most recently seen height in our collection that is greater than the current height
        else:
            ans[i] = height_collection[-1]
        
        # add the current height to the height collection,
        # which is guaranteed to be less than all other heights in the collection
        height_collection.append(curr_height)
            
    return ans

Code implementation confirms process description

The code above closely follows the process described previously; in fact, if we add a simple print statement at the end of each for loop iteration (i.e., after each person has been processed), then we can see this more clearly for ourselves:

print(
    f'Person: {i}; '
    f'Height: {curr_height}; '
    f'Next greater height: {ans[i]}; '
    f'Height collection: {height_collection}; '
    f'Answer so far: {ans}'
)

The console output then confirms the work we did previously (horizontal spacing adjustments added after printing):

Person: 4;  Height: 13;  Next greater height: -1;  Height collection: [13];          Answer so far: [None, None, None, None, -1]
Person: 3;  Height: 14;  Next greater height: -1;  Height collection: [14];          Answer so far: [None, None, None, -1, -1]
Person: 2;  Height: 12;  Next greater height: 14;  Height collection: [14, 12];      Answer so far: [None, None, 14, -1, -1]
Person: 1;  Height: 11;  Next greater height: 12;  Height collection: [14, 12, 11];  Answer so far: [None, 12, 14, -1, -1]
Person: 0;  Height: 12;  Next greater height: 14;  Height collection: [14, 12];      Answer so far: [14, 12, 14, -1, -1]

Approach 2 (left to right, single pass)

The approach described above was kind of clever, specifically how we kept a sort of "history" or collection of previous heights encountered to facilitate the determination of each person's next greater height. Iterating from right to left can sometimes provide a number of advantages, and that's on full display in the solution approach above. But something worth considering is whether or not it's even possible to solve this problem by iterating from left to right in a single pass; that is, we'd like to keep our computational improvement from $O(n^2)$ to $O(n)$ , and we're still willing to compromise on the space requirement from $O(1)$ to $O(n)$ , but we'd like to move from left to right, if possible.

Process intuition

Iterating from left to right to solve the next greater heights problem is possible, but we need to get a little more creative in how we keep track of the heights we've seen thus far to facilitate "next greater height" determinations. Recall the heights we're trying to process: heights = [12, 11, 12, 14, 13]. How we actually start processing peoples' heights from left to right presents a clear problem: what do we do with the first 12 we encounter? When iterating from right to left, it was very clear what to do with the 13 that we encountered on the first iteration: it couldn't possibly have a next greater height (it represented the height of the rightmost person). That's not the case here with the 12 on the first iteration from left to right. It's not just possible for this height to have a next greater height — we know this height has a next greater height of 14, but we need some way of easily determining that. How? What's the strategy?

Part of the strategy harkens back to the intuitive strategy employed in the brute force approach: the next height we see that is greater than the current height becomes the current height's next greater height. If we start with 12, then we cannot yet make a determination about what its next greater height is. So let's just try to "remember" somehow that this height still needs a next greater height.

We could model the situation as follows, where we start by placing an "answer box" below each person's height. The value in the box, if present, represents that person's next greater height. For example, the first person of height 12 would have 14 in its answer box since the next greater height for the first person is the person with a height of 14. Our job is to fill in all answer boxes somehow. The boxes below illustrate this description from our starting state (all empty answer boxes) to our ending state (all answer boxes filled with values reflective of our previous work, which we know to be correct):

Starting state
  12   11   12   14   13 
 ---- ---- ---- ---- ----
|    |    |    |    |    |
 ---- ---- ---- ---- ----

Final state
  12   11   12   14   13 
 ---- ---- ---- ---- ----
| 14 | 12 | 14 | -1 | -1 |
 ---- ---- ---- ---- ----

As noted above, we cannot yet make a determination for the leftmost 12 so we'll simply fill its answer box with ?? until we have more information we can act on:

After first iteration
  12   11   12   14   13 
 ---- ---- ---- ---- ----
| ?? |    |    |    |    |
 ---- ---- ---- ---- ----

In fact, for every current height we encounter, it is not possible for us to know its next greater height yet since we're iterating from left to right. Consequently, each current height we encounter should have its answer box filled with ??. The real question is whether or not any previously encountered heights have the current height as their next greater height; that is, whenever we encounter a new height as the current height, we should look at all heights previously whose answer boxes hold ?? and see if the current height is greater (if so, then this height becomes the next greater height for all such previous heights). This may sound confusing at first, but working out the mechanics for the rest of this example will help clarify the process.

For the new current height of 11, we fill its answer box with ??, and we can see all previous heights whose answer boxes hold ?? (just the leftmost 12 in this case) are not less than 11; hence, no updates are needed and we move on:

After second iteration
  12   11   12   14   13 
 ---- ---- ---- ---- ----
| ?? | ?? |    |    |    |
 ---- ---- ---- ---- ----

Now we encounter the second 12. We fill its answer box with ?? and we look at previous heights whose answer boxes hold ??. The only height less than 12 whose answer box has ?? is the 11 we encountered in the previous iteration. Its next greater height must be 12. We make the update to the answer box for 11 and move on:

After third iteration
  12   11   12   14   13 
 ---- ---- ---- ---- ----
| ?? | 12 | ?? |    |    |
 ---- ---- ---- ---- ----

What about the new height of 14? The heights of 12 encountered previously both have 14 as their next greater height. We make the updates and move on:

After fourth iteration
  12   11   12   14   13 
 ---- ---- ---- ---- ----
| 14 | 12 | 14 | ?? |    |
 ---- ---- ---- ---- ----

For the 13, it is clear no previous height has 13 as its next greater height. Hence, the (almost) final state of the answer boxes is as follows:

After fifth (and final) iteration
  12   11   12   14   13 
 ---- ---- ---- ---- ----
| 14 | 12 | 14 | ?? | ?? |
 ---- ---- ---- ---- ----

The only thing left to do to reach the desired final state is to replace all ?? remaining in answer boxes with -1 (since all such heights have no next greater heights once we've made a full pass iterating from left to right):

Final state
  12   11   12   14   13 
 ---- ---- ---- ---- ----
| 14 | 12 | 14 | -1 | -1 |
 ---- ---- ---- ---- ----

And we're done! How can we get started on translating the process outlined above into an actual code implementation? Two points are probably worthy of consideration before embarking on this task:

-1 autofilling: This is a minor point, but the last step above where we had to convert all remaining ?? to -1 is unnecessary. The solution approach outlined in the previous section autofilled the answer array with None: ans = [None] * len(heights). And that was fine for that solution because the answer slot for every single height was updated to be the next greater height or -1 if no such height existed.

For the process we've described above, however, we only update an answer box if we've found a next greater height; hence, we can simply initialize the answer array with -1 and overwrite answer slots if we find next greater heights.
Updating the next greater height for previous heights based on the current height: This is a more pressing issue. Specifically, the transition from "after the third iteration" to "after the fourth iteration" may raise some eyebrows depending on how we actually plan to do this with code:
After third iteration
12 11 12 14 13 ---- ---- ---- ---- ---- | ?? | 12 | ?? | | | ---- ---- ---- ---- ----
After fourth iteration
12 11 12 14 13 ---- ---- ---- ---- ---- | 14 | 12 | 14 | ?? | | ---- ---- ---- ---- ----
We need to execute this transition efficiently somehow. If we tried updating the answer boxes by iterating from left to right from each height without a next greater height to the current height, then that process would look like the following:
- person 12 has an empty answer box: update to 14
- person 11 has a non-empty answer box: skip
- person 12 has an empty answer box: update to 14
- person 14 is the current height: stop
Imagine if we had to follow the process above every time we encountered a new height. The time complexity would end up being similar to that of the brute force approach. That is not what we want. But for our current consideration we still need to be able to refer to the height values of 12 somehow in order to update their answer boxes to 14. How can we do this as efficiently as possible?

In the previous solution approach, we maintained a collection of heights that decreased from left to right. For example, the collection [14, 12, 11] represented heights that we encountered from oldest to newest, largest to smallest. And we removed smaller heights as needed until we encountered a height greater than the current height. But that approach will not work here. We need to update both answer boxes for the height of 12 — simply keeping a single height of 12 in some sort of collection will not suffice because there's no way to distinguish between these two heights based on value alone.

How can we make a distinction between two heights that have the same numeric value? Consider the original input array: heights = [12, 11, 12, 14, 13]. It may be true that heights[0] == heights[2] (i.e., 12 == 12), but it's certainly not the case that 0 == 2; that is, the index values of the heights make each height uniquely distinct. What if instead of keeping a collection of heights for reference we kept a collection of index values for previously encountered heights? Index values make it possible to access both a height's numeric value as well as where its answer box needs to be updated (i.e., its indexed position). This might be just what we need.

Process description

If we started processing the height of each person from the left using the process alluded to above, where we kept track of index values for previously encountered heights, then what would each step of the process look like? Let's draw this up in tabular form, as with the previous solution approach (the people-indexing is 0-based), first recalling the heights of the people to be processed, heights = [12, 11, 12, 14, 13]. (An index-to-height correspondence array is provided in the table below to help clarify what heights correspond to which indexes.)

Person	Height	Process Description
`0`	`12`	This is the leftmost person, and the collection of index values for previously encountered heights is currently empty. Hence, we add the current height's index value to the collection: `[0]`. Collection's index-to-height correspondence: `[12]`. Current answer array: `[-1, -1, -1, -1, -1]`.
`1`	`11`	The current height is now `11`. Are there any index values in the collection that represent a height less `11`? No. We now add the current height's index value to the collection: `[0, 1]`. Collection's index-to-height correspondence: `[12, 11]`. Current answer array: `[-1, -1, -1, -1, -1]`.
`2`	`12`	The current height is now `12`. Are there any index values in the collection that represent a height less than `12`? Yes. Our current collection is `[0, 1]`, and the index value of `1` corresponds to a height of `11`. We update the corresponding slot in the answer array by using our collection of index values (i.e., the next greater height for the person with height `11` is the current height of `12`): `ans[1] = 12`. We now remove `1` from the collection since the person's next greater height at this position has now been determined. Current collection: `[0]`. Is the height of the person at index `0` less than the current height of `12`? No. We now add the current height's index value to the collection: `[0, 2]`. Collection's index-to-height correspondence: `[12, 12]`. Current answer array: `[-1, 12, -1, -1, -1]`.
`3`	`14`	The current height is now `14`. Are there any index values in the collection that represent a height less than `14`? Yes. Our current collection is `[0, 2]`, and the index value of `2` corresponds to a height of `12`. We update the corresponding answer slot by using our collection of index values (i.e., the next greater height for the person at index `2` with height `12` is the current height of `14`): `ans[2] = 14`. We now remove `2` from the collection since the person's next greater height at this position has now been determined. Current collection: `[0]`. Is the height of the person at index `0` less than the current height of `14`? Yes. We update the corresponding answer slot by using our collection of index values: `ans[0] = 14`. We now remove `0` from the collection since the person's next greater height at this position has now been determined. Current collection: `[]`. The collection is now empty so we have no previous heights to compare with the current height. We now add the current height's index value to the collection: `[3]`. Collection's index-to-height correspondence: `[14]`. Current answer array: `[14, 12, 14, -1, -1]`.
`4`	`13`	The current height is now `13`. Are there any index values in the collection that represent a height less than `13`? No. We now add the current height's index value to the collection: `[3, 4]`. Collection's index-to-height correspondence: `[14, 13]`. Current answer array: `[14, 12, 14, -1, -1]`. We have now finished processing the heights for all people. The final answer array is `[14, 12, 14, -1, -1]`, as desired.

As before, it may be illustrative to show a condensed table where the reported next greater height for each person is included as well as what our reference collection of index values looks like after processing each person (along with the heights that correspond to these index values):

Person	Height	Index collection after person processed	Index-height correspondence	Answer array
`0`	`12`	`[0]`	`[12]`	`[-1, -1, -1, -1, -1]`
`1`	`11`	`[0, 1]`	`[12, 11]`	`[-1, -1, -1, -1, -1]`
`2`	`12`	`[0, 2]`	`[12, 12]`	`[-1, 12, -1, -1, -1]`
`3`	`14`	`[3]`	`[14]`	`[14, 12, 14, -1, -1]`
`4`	`13`	`[3, 4]`	`[14, 13]`	`[14, 12, 14, -1, -1]`

The table above shows more clearly how the answer array is updated in conjunction with index values being removed from our collection; that is, for example, after person 2 was processed, we removed index 1 from our collection and updated the value at index 1 in the answer array to be equal to the height of the current person being processed, the next greater height for the person at index 1, namely the height of 12.

Code implementation

Now for the code implementation of the process described above:

def next_greater_height_2(heights):
    height_collection = []
    ans = [-1] * len(heights)
    
    for i in range(len(heights)):
        curr_height = heights[i]

        # remove all index values in our collection that correspond to
        # previously encountered heights less than the current height
        # (and then update the answer array to point to the curren height as
        # the next greater height for the people positioned at those index values)
        while height_collection and heights[height_collection[-1]] < curr_height:
            prev_height_index = height_collection.pop()
            ans[prev_height_index] = curr_height

        # add the index for the current person's height to the collection,
        # which is guaranteed to correspond to a height less than all
        # other correspondent heights in the index collection
        height_collection.append(i)
    
    return ans

Code implementation confirms process description

The code above closely follows the process described previously; in fact, if we add a simple print statement at the end of each for loop iteration (i.e., after each person has been processed), then we can see this more clearly for ourselves:

print(
    f'Person: {i}; '
    f'Height: {heights[i]}; '
    f'Index collection: {index_collection}; '
    f'Index-height correspondence: {[heights[i] for i in index_collection]}; '
    f'Answer array: {ans}'
)

The console output then confirms the work we did previously (horizontal spacing adjustments added after printing):

Person: 0;  Height: 12;  Index collection: [0];     Index-height correspondence: [12];      Answer array: [-1, -1, -1, -1, -1]
Person: 1;  Height: 11;  Index collection: [0, 1];  Index-height correspondence: [12, 11];  Answer array: [-1, -1, -1, -1, -1]
Person: 2;  Height: 12;  Index collection: [0, 2];  Index-height correspondence: [12, 12];  Answer array: [-1, 12, -1, -1, -1]
Person: 3;  Height: 14;  Index collection: [3];     Index-height correspondence: [14];      Answer array: [14, 12, 14, -1, -1]
Person: 4;  Height: 13;  Index collection: [3, 4];  Index-height correspondence: [14, 13];  Answer array: [14, 12, 14, -1, -1]

Approach 3 (single pass, modified question)

Was all of the pain and suffering involved in hammering out the approach above worth it? Maybe. The truth is that many problems won't just be about what an element's next greater or smaller element is; instead, the problem will have something to do with how these elements relate to each other in some way.

Modifed problem statement

For example, for the "next greater height" problem we've been considering, what if the question were tweaked slightly to not be about what a height's next greater height is but how many spaces there are between people with these heights?

Modified solution

Consider again how the people are lined up:

Given the heights [12, 11, 12, 14, 13], we know from our previous work that each height's next greater height is given by [14, 12, 14, -1, -1], where -1 conveys there is no next greater height for the height of the person at that position. If the answer array is now comprised of values that denote how many spaces there are between the current person and the person with the next greater height, then our answer array becomes [3, 1, 1, 0, 0], where 0 conveys the person at that position does not have someone to their right with a greater height.

How is it possible to assemble this answer array? Do we have to significantly revise our previous solution approach(es)? No. In fact, the second approach above, where we used a collection of index values, gives us all we need because the positional information we need for each person is provided by the index values themselves:

Person 0: When we encounter the next greater height of 14, we note that this next greater height occurs at position or index 3 (i.e., heights[3] == 14). The current height of 12 for person 0 occurs at position or index 0 (here we can take advantage of the fact that the numeric label for each person corresponds to the index value of the corresponding height; that is, person x will have height heights[x]). We can use the difference in index values to compute how many spaces there are between these people: 3 - 0 = 3.
Person 1: Current height of 11 occurs at index 1 and next greater height of 12 occurs at index 2. The number of spaces between these people: 2 - 1 = 1.
Person 2: Current height of 12 occurs at index 2 and next greater height of 14 occurs at index 3. The number of spaces between these people: 3 - 2 = 1.
Person 3: Current height of 14 occurs at index 3 and there is no next greater height; hence, report 0.
Person 4: Current height of 13 occurs at index 4 and there is no next greater height; hence, report 0.

That's it. That's all there is to do. The code modifications required, hightlighted below, are quite minor:

Approach 3 (spaces between people)
def next_greater_height_3(heights):
    index_collection = []
    ans = [0] * len(heights)
    
    for i in range(len(heights)):
        curr_height = heights[i]
        while index_collection and heights[index_collection[-1]] < curr_height:
            prev_height_index = index_collection.pop()
            spaces_between = i - prev_height_index
            ans[prev_height_index] = spaces_between
        index_collection.append(i)
    
    return ans

Approach 2 (next greater height)
def next_greater_height_2(heights):
    index_collection = []
    ans = [-1] * len(heights)
    
    for i in range(len(heights)):
        curr_height = heights[i]
        while index_collection and heights[index_collection[-1]] < curr_height:
            prev_height_index = index_collection.pop()
            ans[prev_height_index] = curr_height

        index_collection.append(i)
    
    return ans

LC 739. Daily Temperatures

Problem statement

Let's now turn our attention to LC 739. Daily Temperatures for some practice. Here's the problem statement for ease of reference:

Given an array of integers temperatures that represents the daily temperatures, return an array answer such that answer[i] is the number of days you have to wait after the ith day to get a warmer temperature. If there is no future day for which this is possible, keep answer[i] == 0 instead.

For example, if temperatures = [73,74,75,71,69,72,76,73] is given as input, then the desired output would be as follows: [1,1,4,2,1,1,0,0].

Solution

This is virtually the same problem as the modified question for the next greater height problem where we looked at the number of spaces between each person and the next person of greater height. The solution to this LeetCode problem is almost identical (except here we're dealing with temperatures instead of heights, of course):

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        index_collection = []
        answer = [0] * len(temperatures)
        
        for i in range(len(temperatures)):
            curr_temp = temperatures[i]
            while index_collection and temperatures[index_collection[-1]] < curr_temp:
                prev_temp_index = index_collection.pop()
                days_between = i - prev_temp_index
                answer[prev_temp_index] = days_between
            index_collection.append(i)
        
        return answer

Arguably the main challenge for this problem (and most other kinds of problems) is to actually identify that our solution approach is relevant and then to implement it without issues. That's often where the real difficulty lies.

Sliding window minimum

Let's try one last problem before bothering ourselves with technical terms and concepts: the sliding window minimum problem.

Problem statement

You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Return an answer array that contains the minimum value for each sliding window of size k.

For example, if the input array is nums = [11, 13, -11, -13, 15, 13, 16, 17] and k = 3, then the desired output or answer array would be [-11, -13, -13, -13, 13, 13]:

Window position Min ------------------------ ----- [11 13 -11] -13 15 13 16 17 -11 11 [13 -11 -13] 15 13 16 17 -13 11 13 [-11 -13 15] 13 16 17 -13 11 13 -11 [-13 15 13] 16 17 -13 11 13 -11 -13 [15 13 16] 17 13 11 13 -11 -13 15 [13 16 17] 13

False start

In the next greater height problem at the beginning of this post, we saw that it was an effective strategy to maintain a collection that we could use to reference previously encountered heights where the collection was comprised of either the heights themselves (Approach 1) or indexes that we could use to obtain the heights themselves (Approach 2). For both approaches, the collections we maintained effectively corresponded to heights that were weakly decreasing (i.e., values that were decreasing or possibly equivalent).

Approach 1: The height collections after processing people 4, 3, 2, 1, and 0 were as follows, respectively:
- [13]
- [14]
- [14, 12]
- [14, 12, 11]
- [14, 12]
Approach 2: The index collections after processing people 0, 1, 2, 3, and 4 were as follows, respectively (height correspondence shown to the right):
${\small \begin{array}{lcl} \texttt{[0]} &\longrightarrow & \texttt{[12]}\\ \texttt{[0, 1]} &\longrightarrow & \texttt{[12, 11]}\\ \texttt{[0, 2]} &\longrightarrow & \texttt{[12, 12]}\\ \texttt{[3]} &\longrightarrow & \texttt{[14]}\\ \texttt{[3, 4]} &\longrightarrow & \texttt{[14, 13]} \end{array}}$

As demonstrated above, the heights we could reference by means of these collections we were maintaining in both approaches were weakly decreasing (strictly decreasing in Approach 1 and weakly decreasing in Approach 2). Specifically, the heights in the collection progressed from largest to smallest and went from "oldest" to "newest"; that is, the leftmost height was encountered before any other heights that followed, and the "newest" height was always the current height we just encountered.

The last part in the sentence above bears repeating because it indicates how we actually go about maintaining the collection: the "newest" height was always the current height we just encountered. If the collection of heights is decreasing and the current height is always the newest height in the collection, then this means we need to keep removing heights from the collection until the current height is the smallest one. Doing so ensures we maintain the "collection is decreasing" invariant. For example, if our height collection is [18, 16, 14, 11, 8, 4] and we encounter a new height of 13, then we need to remove every element of the collection less than 13 before we add this "newest" current height: [18, 16, 14, 13].

How does all of this help for the current problem of finding the minimum value in each three-element sliding window as we move from left to right? Since we're interested in the minimum value for each window and the rightmost value in the collections we maintained previously was always the smallest value, maybe this means we could dynamically maintain a "window collection" where we always picked off the rightmost value as the minimum? Let's try (first recall our input array: nums = [11, 13, -11, -13, 15, 13, 16, 17]):

The first value is 11 with index 0. Right now our collection is empty and the window is not yet of size k = 3. Hence, we add 0 to our collection and proceed. Current collection: [0].
The second value is 13 with index 1. Our collection right now is [0] which corresponds to the value of 11. Oops. We've already run into a problem: what do we do with index 1 that corresponds to value 13? If we add it to the collection, then we'll actually need to remove what's currently in the collection to maintain the "collection is decreasing" invariant. Our collection would go from [0] to [1], which corresponds to the value of [13], and this respects the "decreasing invariant" of our collection. If we did not remove 0 from our collection before adding 1, then our collection would be [0, 1], which corresponds to values [11, 13], and that would violate the "decreasing invariant" of our collection.

Simply removing index 0 from our collection is really not an option here. If the first three elements of the input array were, for example, [11, 13, 12], then removing the ability to reference 11 means we've actually lost the ability to accurately determine the minimum value for the first three-element window.

We need a different strategy. What if our collection referred to increasing values from left to right instead of decreasing values? Then the leftmost value would now be the smallest value (i.e., minimum) and we would not have to remove it whenever we encountered a larger value. Let's try again (input array for quick reference: nums = [11, 13, -11, -13, 15, 13, 16, 17]):

The first value is 11 with index 0. Right now our collection is empty and the window is not yet of size k = 3. Hence, we add 0 to our collection and proceed. Current collection: [0].
The second value is 13 with index 1. Our collection right now is [0] which corresponds to value [11]. Since 13 is greater than 11, we can simply add its index to our collection and proceed. Current collection: [0, 1].
The third value is -11 with index 2. Our collection right now is [0, 1] which corresponds to values [11, 13]. But we want our collection to be increasing, where each newly added index corresponds to the greatest value referenced in the collection. To accommodate the addition of -11 to our collection (while maintaining the "increasing invariant"), we need to remove all indexes from our collection that correspond to values smaller than -11, namely all indexes in this case since both 11 and 13 are greater than -11. Our new collection becomes [2] which corresponds to value [-11]. Also, since we've now encountered the third value, we now have a 3-element window, and its minimum is the leftmost value referenced by our collection (i.e., nums[2] == -11).

This strategy seems like it might work. Let's write things out in tabular form as we did with the previous approaches, where this time we'll have six columns (each row's column values will refer to the state of things after the current indexed value has been processed):

Index: This is the index of the value being processed.
Value: This is the value that corresponds to the row's index value.
Index collection: This is the increasing index collection (i.e., indexes correspond to values that increase from smaller to larger).
Index-value correspondence: Translation of indexes in the collection to their correspondent values (for ease of reference).
Window indexes: We're told that the window is of size k = 3 and moves one unit from left to right. Hence, the sliding window indexes are [0, 1, 2] for the first window, [1, 2, 3] for the second window, and so on. This should be useful as a sanity check to ensure we don't include as a window minimum a value that is not actually in the window!
Window minimum: This is the minimum value for the current window of size k = 3.

First recall our input: nums = [11, 13, -11, -13, 15, 13, 16, 17], k = 3. Now let's try to implement the strategy discussed above in tabular form:

Index	Value	Index collection	Index-value correspondence	Window indexes	Window minimum
`0`	`11`	`[0]`	`[11]`	`[0, x, x]`
`1`	`13`	`[0, 1]`	`[11, 13]`	`[0, 1, x]`
`2`	`-11`	`[2]`	`[-11]`	`[0, 1, 2]`	`-11`
`3`	`-13`	`[3]`	`[-13]`	`[1, 2, 3]`	`-13`
`4`	`15`	`[3, 4]`	`[-13, 15]`	`[2, 3, 4]`	`-13`
`5`	`13`	`[3, 5]`	`[-13, 13]`	`[3, 4, 5]`	`-13`
`6`	`16`	`[3, 5, 6]`	`[-13, 13, 16]`	`[4, 5, 6]`	`-13`

Oh no. The strategy seemed to be working great, but the last row above cannot be correct — the index of 3 in the index collection [3, 5, 6] is not valid when we encounter index 6 because the window of length k = 3 with index 6 as its right endpoint has the following indexes: [4, 5, 6]. We've included an invalid index!

Is the strategy we were working on implementing above in tabular form completely doomed? Do we need to pursue a different strategy altogether? Or can we make a slight adjustment to fix everything?

Fixed start

Fortunately, the exact issue of what went wrong in the last row above is easy to identify: the index collection we were maintaining has an index value that is invalid for the sliding window; that is, when our sliding window of length k = 3 ends at index 6, this means the sliding window extends across indexes [4, 5, 6]. The index 3 is thus invalid. What should we do? What if we just removed this invalid index from our collection? Would that work? If we removed only the invalid index, then our collection would become [5, 6], which would correspond to values [13, 16]. Does this work?

The sliding window that extends across indexes [4, 5, 6] corresponds to the following values: [15, 13, 16]; hence, the minimum value for this window is 13, which occurs at index 5. And this is now the leftmost value in our index collection since we only removed the invalid index! This isn't just a happy coincidence or chance.

Recall that for each new value we encounter, we ensure it is the largest value referred to in our index collection, where are our index collection represents corresponding values that increase. Furthermore, what's the largest size our index collection should ever possibly be? Answer: The size of the sliding window, k. Why? If the index collection were larger than the size of the sliding window itself, k = 3 in this case, then our collection would automatically have an invalid index. So how do we ensure the index collection never exceeds a size of k and only ever has valid indexes? The manner in which the sliding window moves is a hint.

Once the initial window size of k has been reached, every time the window shifts a single unit to the right, the window's previous leftmost index must be removed as a valid index from our index collection (if it is present); that is, if i is the index of the value we have currently processed to maintain our collection's increasing or decreasing invariant, and our sliding window is of size k, then the leftmost index that must be removed (if it is part of our collection) is i - k. For example, if i = 7, and k = 3, then the valid window indexes are [5, 6, 7], and the leftmost index of the previous window which is no longer valid and would need to be removed from our collection (if it was present) would be i - k = 7 - 3 = 4.

When can the scenario described above actually happen? This can happen when the index in need of removal corresponds to the minimum value for k windows of size k, and this is exactly what happened when we were progressing through the table above when we encountered our issue:

Indexes [1, 2, 3] corresponded to values [13, -11, -13]. Minimum: -13 (index 3).
Indexes [2, 3, 4] corresponded to values [-11, -13, 15]. Minimum: -13 (index 3).
Indexes [3, 4, 5] corresponded to values [-13, 15, 13]. Minimum: -13 (index 3).
Indexes [4, 5, 6] corresponded to values [15, 13, 16]. Minimum: 13, not -13 (index 5, not 3).

The value nums[3] == -13 was the minimum value for k = 3 windows. This index value is no longer valid for this window because it was the leftmost index of the previous window.

How do we "just remove" the invalid index of 3 when our increasing index collection of [3, 5, 6] corresponds to values [-13, 13, 16] even though the sliding window only covers indexes [4, 5, 6] which corresponds to values [15, 13, 16]? In all of the approaches thus far, we have always added/removed values to/from our collection from the right in order to maintain the collection's increasing or decreasing invariant as well as the order in which we've encountered elements ("oldest" to "newest" from left to right, respectively). We are still doing that in this approach that we've been describing, but what's to stop us from removing invalid values in our collection from the left (when needed)?

Removing 3 from the left of [3, 5, 6] means we now have [5, 6] (correspondent values [13, 16]), which are valid window indexes for the window that extends across indexes [4, 5, 6]. Hence, removing an element from the left did not disturb the increasing invariant of our collection that we've been trying to maintain — we simply removed an invalid value. The reward is that the new leftmost index in our collection, 5, corresponds to the minimum value of the current three-element window: nums[5] == 13.

Let's try our tabular approach again, but this time we'll remove invalid indexes from the left of our collection if we encounter them before reporting a window minimum:

Index	Value	Index collection	Index-value correspondence	Window indexes	Index to remove (if present)	Window minimum
`0`	`11`	`[0]`	`[11]`	`[0, x, x]`
`1`	`13`	`[0, 1]`	`[11, 13]`	`[0, 1, x]`
`2`	`-11`	`[2]`	`[-11]`	`[0, 1, 2]`		`-11`
`3`	`-13`	`[3]`	`[-13]`	`[1, 2, 3]`	`3 - 3 = 0 != 3`	`-13`
`4`	`15`	`[3, 4]`	`[-13, 15]`	`[2, 3, 4]`	`4 - 3 = 1 != 3`	`-13`
`5`	`13`	`[3, 5]`	`[-13, 13]`	`[3, 4, 5]`	`5 - 3 = 2 != 3`	`-13`
`6`	`16`	`[5, 6]`	`[13, 16]`	`[4, 5, 6]`	`6 - 3 = 3 == 3` (removed)	`13`
`7`	`17`	`[5, 6, 7]`	`[13, 16, 17]`	`[5, 6, 7]`	`7 - 3 = 4 != 5`	`13`

If we collect the window minimums from the table above into an array, then we get [-11, -13, -13, -13, 13, 13], as desired.

Code implementation

Now for the code implementation of the process described above:

def sliding_window_min_1(nums, k):
    index_collection = []
    ans = []
    
    for i in range(len(nums)):
        curr_num = nums[i]

        # remove all index values in our collection that correspond to
        # previously encountered numbers greater than the current number
        # (note that removals are made from the right)
        while index_collection and nums[index_collection[-1]] > curr_num:
            index_collection.pop()
        
        # add the index for the current number to the collection,
        # which is guaranteed to correspond to a number greater than all
        # other correspondent numbers in the index collection;
        # importantly, the leftmost index of the collection corresponds 
        # to the smallest number represented in the collection
        # (note that additions are made to the right)
        index_collection.append(i)
        
        # if the leftmost index in our collection corresponds 
        # to the leftmost index of the previous window, 
        # then remove this index in the collection _from the left_
        if index_collection[0] == i - k:
            index_collection.pop(0)
        
        # do not start adding window minimums to the answer array
        # until our window has reached a size of k
        if i >= k - 1:
            ans.append(nums[index_collection[0]])
            
    return ans

The highlighted lines above are meant to serve as warnings in a way. Why? The code above clearly provides the correct output and respects every detail of our process and strategy:

print(sliding_window_min_1([11, 13, -11, -13, 15, 13, 16, 17], 3))
# [-11, -13, -13, -13, 13, 13]

The reason why the lines above are highlighted in warning colors is because of the data structure we are using for our index_collection, namely a Python list or "dynamic array." Python lists are excellent if we're mostly adding or removing elements from the end (i.e., the right) because these operations are $O(1)$ on average. We're executing such operations whenever we move to a new index and add it to the index_collection — we remove all indexes from the right of the collection until the only remaining indexes correspond to values less than or equal to the current value. But what if we then discover that the leftmost index in our collection is the leftmost index of the previous window and is therefore an invalid index? We remove this index in our collection from the left.

Removing elements in arrays from the left on a regular basis is not performant because each removal is $O(n)$ , where $n$ represents the number of elements in the array (all array elements need to be shifted in memory once the first element is deleted). It would be ideal if we could use a data structure that supported efficient additions/removals from the right and from the left. What we're looking for is the so-called double-ended queue or "deque" for short, and Python has just the thing in its collections module: collections.deque:

class collections.deque([iterable[, maxlen]])

Returns a new deque object initialized left-to-right (using append()) with data from iterable. If iterable is not specified, the new deque is empty.

Deques are a generalization of stacks and queues (the name is pronounced "deck" and is short for "double-ended queue"). Deques support thread-safe, memory efficient appends and pops from either side of the deque with approximately the same $O(1)$ performance in either direction.

Though list objects support similar operations, they are optimized for fast fixed-length operations and incur $O(n)$ memory movement costs for pop(0) and insert(0, v) operations which change both the size and position of the underlying data representation.

[...]

As noted on Stack Overflow and confirmed in CPython's source code, the deque in Python is implemented under the hood with a doubly-linked list. A comment on a separate Stack Overflow thread summarizes the takeaway rather neatly:

In my case, the time went down from 1:31 min. with pop(0) to 200 - 250 ms by using deque.

If we're going to be regularly adding and removing elements from the left and from the right, which is all we're actually doing with our index_collection in the solution above, then the data structure we should use is a double-ended queue. The code changes required, highlighted below, are minimal for the optimal solution:

# import the deque from the collections module in Python's standard library
from collections import deque

def sliding_window_min_2(nums, k):
    # initialize empty deque for O(1) additions/removals from both ends
    index_collection = deque()
    ans = []
    
    for i in range(len(nums)):
        curr_num = nums[i]
        while index_collection and nums[index_collection[-1]] > curr_num:
            index_collection.pop()
        index_collection.append(i)

        if index_collection[0] == i - k:
            # remove elements from the left in O(1) time
            index_collection.popleft()
        
        if i >= k - 1:
            ans.append(nums[index_collection[0]])
            
    return ans

It's worth noting that, until now with the advent of a double-ended queue for the optimal solution above, we have not explicitly mentioned using stacks or queues in any of our problem-solving approaches, much less "monotonic" stacks or queues. And that's because we haven't really needed to use that terminology — we used the ideas without knowing the names for these ideas. All of the terminology will soon be defined and made clear (once we wrap up this sliding window problem).

Code implementation confirms process description

The code above closely follows the process described previously; unfortunately, in this case, adding a print statement after each for loop (i.e., after each index has been processed) is not as simple as it was in the previous problem. Nonetheless, if you want to modify the solution code to accomplish this, then you can.

Modified solution code to print tabular values for each iteration

def sliding_window_min_2_print(nums, k):
    index_collection = deque()
    ans = []
    
    for i in range(len(nums)):
        removing_index = False
        window_min_exists = False
        curr_num = nums[i]
        while index_collection and nums[index_collection[-1]] > curr_num:
            index_collection.pop()
        index_collection.append(i)
        
        if index_collection[0] == i - k:
            removing_index = True
            removed_index = index_collection.popleft()
            
        if i >= k - 1:
            window_min_exists = True
            window_min = nums[index_collection[0]]
            ans.append(nums[index_collection[0]])
            
        print(
            f'Index: {i}; '
            f'Value: {nums[i]}; '
            f'Index collection: {list(index_collection)}; '
            f'Index-value correspondence: {[nums[idx] for idx in index_collection]}; '
            f'Window indexes: {[0, "x", "x"] if i == 0 else [0, 1, "x"] if i == 1 else [ val + (i - k) for val in range(1, k + 1)]}; '
            f'Index to remove (if present): {i} - {k} = {i - k} {"==" if removing_index else "!="} {removed_index if removing_index else index_collection[0]} {"(removed)" if removing_index else ""}; '
            f'Window minimum: {window_min if window_min_exists else ""}'
        )
            
    return ans

The console output then confirms the work we did previously (horizontal spacing adjustments added after printing):

Index: 0;  Value:  11;  Index collection: [0];        Index-value correspondence: [11];          Window indexes: [0, 'x', 'x'];   Index to remove (if present): 0 - 3 = -3 != 0;            Window minimum: 
Index: 1;  Value:  13;  Index collection: [0, 1];     Index-value correspondence: [11, 13];      Window indexes: [0, 1, 'x'];     Index to remove (if present): 1 - 3 = -2 != 0;            Window minimum: 
Index: 2;  Value: -11;  Index collection: [2];        Index-value correspondence: [-11];         Window indexes: [0, 1, 2];       Index to remove (if present): 2 - 3 = -1 != 2;            Window minimum: -11
Index: 3;  Value: -13;  Index collection: [3];        Index-value correspondence: [-13];         Window indexes: [1, 2, 3];       Index to remove (if present): 3 - 3 = 0  != 3;            Window minimum: -13
Index: 4;  Value:  15;  Index collection: [3, 4];     Index-value correspondence: [-13, 15];     Window indexes: [2, 3, 4];       Index to remove (if present): 4 - 3 = 1  != 3;            Window minimum: -13
Index: 5;  Value:  13;  Index collection: [3, 5];     Index-value correspondence: [-13, 13];     Window indexes: [3, 4, 5];       Index to remove (if present): 5 - 3 = 2  != 3;            Window minimum: -13
Index: 6;  Value:  16;  Index collection: [5, 6];     Index-value correspondence: [13, 16];      Window indexes: [4, 5, 6];       Index to remove (if present): 6 - 3 = 3  == 3 (removed);  Window minimum: 13
Index: 7;  Value:  17;  Index collection: [5, 6, 7];  Index-value correspondence: [13, 16, 17];  Window indexes: [5, 6, 7];       Index to remove (if present): 7 - 3 = 4  != 5;            Window minimum: 13

LC 239. Sliding Window Maximum

Problem statement

Let's now turn our attention to LC 239. Sliding Window Maximum for some practice. Here's the problem statement for ease of reference:

You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position.

Return the max sliding window.

For example, if nums = [1,3,-1,-3,5,3,6,7], k = 3 is given as input, then the desired output would be as follows: [3,3,5,5,6,7]. The following illustration can help us see this more clearly (just like we did for the sliding window minimum problem earlier):

Window position                Max

---------------               -----

[1  3  -1] -3  5  3  6  7       3

 1 [3  -1  -3] 5  3  6  7       3

 1  3 [-1  -3  5] 3  6  7       5

 1  3  -1 [-3  5  3] 6  7       5

 1  3  -1  -3 [5  3  6] 7       6

 1  3  -1  -3  5 [3  6  7]      7

Solution

The problem above is virtually identical to the sliding window minimum problem we worked so hard to solve. In fact, the only difference is that now we're looking for the maximum of each window instead of the minimum. This means the index_collection we maintain should be decreasing (so that the leftmost value will always be a maximum). The rest of the logic stays the exact same. Hence, the only thing we need to do is change the comparison in the while loop from > to <; that is, we need to change

while index_collection and nums[index_collection[-1]] > curr_num:

while index_collection and nums[index_collection[-1]] < curr_num:

Everything else stays as it was in our original solution:

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        index_collection = deque()
        ans = []
        
        for i in range(len(nums)):
            curr_num = nums[i]
            while index_collection and nums[index_collection[-1]] < curr_num:
                index_collection.pop()
            index_collection.append(i)
            
            if index_collection[0] == i - k:
                index_collection.popleft()
                
            if i >= k - 1:
                ans.append(nums[index_collection[0]])
                
        return ans

Interestingly, we can actually get away with not using a deque here (i.e., we just use a list instead and left removals cost more computationally than they might otherwise). The answer is still accepted by LeetCode even though it's notably slower than the solution using a deque. The test cases LeetCode uses are not public/visible, but presumably the reason the list-based solution is still acceptable is because most operations on index_collection are additions and removals from the right, where these list operations are still $O(1)$ . Only on certain occasions do we need to remove an element from the left, which will be $O(k)$ instead of $O(1)$ since the largest size of the index collection we're maintaining is of size $k$ .

We should note that the performance concern remarked on above (i.e., $O(k)$ left-removals instead of $O(1)$ ) pales in comparison to the most significant computational gains of crafting a solution that performs in $O(n)$ with a single pass instead of processing every single subarray on its own in a brute force fashion, which would be $O(n^2)$ . That kind of solution would definitely not be accepted for this hard problem.

List-based solution to LC 239 that is less performant than deque-based solution but accepted nonetheless

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        index_collection = []
        ans = []

        for i in range(len(nums)):
            curr_num = nums[i]
            while index_collection and nums[index_collection[-1]] < curr_num:
                index_collection.pop()
            index_collection.append(i)

            if index_collection[0] == i - k:
                index_collection.pop(0)

            if i >= k - 1:
                ans.append(nums[index_collection[0]])

        return ans

Monotonic stacks and queues (deques)

Definition of "monotonic"

Mathematical background (not necessary but still helpful)

The Wiki article on monotonic functions is surprisingly helpful. The relevant portions have been reproduced below (with slight adjustments).

A function $f$ defined on a subset of the real numbers with real values is said to be monotonic if and only if $f$ is either entirely non-increasing or entirely non-decreasing:

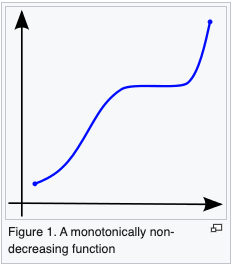
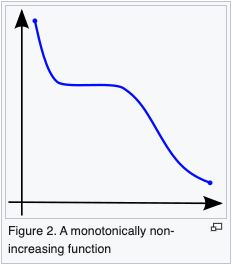
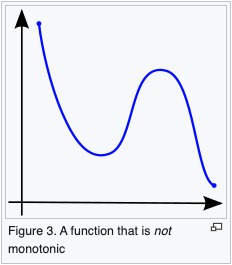
A function is said to be monotonically increasing (also increasing or non-decreasing) if for all $x$ and $y$ such that $x\leq y$ one has $f(x)\leq f(y)$ , so $f$ preserves the order (Figure 1). Likewise, a function is said to be monotonically decreasing (also decreasing or non-increasing) if, whenever $x\leq y$ , then $f(x)\geq f(y)$ , so it reverses the order (Figure 2).

If the order $\leq$ in the definition of monotonicity is replaced by the strict order $<$ , one obtains a stronger requirement. A function with this property is said to be strictly increasing (also increasing). Again, by inverting the order symbol, one finds a corresponding concept called strictly decreasing (also decreasing). A function with either property is called strictly monotone.

To avoid ambiguity, the terms weakly monotone, weakly increasing and weakly decreasing are often used to refer to non-strict monotonicity.

The terms "non-decreasing" and "non-increasing" should not be confused with the (much weaker) negative qualifications "not decreasing" and "not increasing". For example, the non-monotonic function shown in Figure 3 first falls, then rises, then falls again. It is therefore not decreasing and not increasing, but it is neither non-decreasing nor non-increasing.

Let's first provide a working definition of the word monotonic:

Mathematics. (of a function or sequence) either consistently increasing in value and never decreasing, or consistently decreasing in value and never increasing:

A monotonic sequence can either converge or diverge, but it can never oscillate.

In the context of programming, we're generally concerned with a collection or "sequence" of values (as opposed to a function). Whether or not the sequence is deemed monotonic depends on how the values relate to each other in progression from left to right:

Strictly decreasing (each value is less than all preceding values)
Weakly decreasing (each value is less than or equal to all preceding values)
Strictly increasing (each value is greater than all preceding values)
Weakly increasing (each value is greater than or equal to all preceding values)

Basic code examples are illustrative in clarifying these definitions:

Strictly decreasing
[14, 13, 12, 11, 8, 6]

Weakly decreasing
[14, 13, 13, 12, 12, 11, 8, 6]

Strictly increasing
[-13, 13, 16, 18, 21]

Weakly increasing
[-13, 13, 13, 16, 18, 18, 18, 21]

Important observations due to "monotonic" definition

Avoid this section at your own risk!

This section is, without question, the most important section in this entire post. The observations detailed below serve as the foundation for all subsequently solved problems as well as all templates. Take whatever time is necessary to grok these important observations!

There are several important observations worth noting that stem directly from the definitions illustrated above:

Unique or duplicate values: "Strictly decreasing" and "strictly increasing" are both strict (all values are unique) whereas their "weak" variants are not (adjacent values may be equal which means duplicate values are permitted). The following terms are equivalent (I personally use the strict/weak terminology because I find them to be clearer than their alternatives):
```
Strictly increasing  =  increasing
Weakly increasing    =  non-decreasing

Strictly decreasing  =  decreasing
Weakly decreasing    =  non-increasing
```
Alternate terminology for "weakly": Sometimes the terms non-decreasing and non-increasing are used instead of weakly increasing and weakly decreasing, respectively (as shown above). Unfortunately, while such terminology is technically accurate, it arguably obscures the important behavior being highlighted; that is, for a sequence like [1, 2, 2, 3], calling it "non-decreasing" arguably obscures what we actually want to highlight, namely that the collection is increasing except when adjacent values can be equal. Saying the collection is "weakly increasing" seems to be a better choice of words.

It's also arguably clearer to use the words "strictly increasing" instead of just "increasing" so as to be completely unambiguous.
Minimum/maximum values: If a sequence is strictly decreasing or weakly decreasing, then the leftmost value represents the maximum value in the collection. Similarly, if a sequence is strictly increasing or weakly increasing, then the leftmost value represents the minimum value in the collection.
Monotonicity invariant: The definition for invariant is what it sounds like:

Mathematics. a quantity or expression that is constant throughout a certain range of conditions.

The idea of an invariant in computer science is effectively the same but slightly nuanced:

In computer science, an invariant is a logical assertion that is always held to be true during a certain phase of execution of a computer program. For example, a loop invariant is a condition that is true at the beginning and the end of every iteration of a loop.

How is the idea of an invariant relevant to our work with monotonic stacks and queues? Imagine adding 3 to the weakly increasing monotonic stack [0, 1, 1, 4] without first removing any elements: [0, 1, 1, 4, 3]. The weakly increasing monotonic stack we had previously is now just a stack because its special property of monotonicity has been violated. "Maintaining" a monotonic stack or deque really means maintaining its invariant: monotonicity. The (weakly) increasing/decreasing stack or deque should remain (weakly) increasing/decreasing whenever elements are added or removed.
Adding elements: As noted above, special care must be taken when adding values to a monotonic stack or deque to ensure its monotonicity invariant remains intact. Specifically, adding value x means first removing all other values that would cause the invariant to be broken should x be added to the stack or queue in its current state — only then should x be added. Since the collection of values being maintained is a stack or deque, additions generally happen from the right. (If we are using a double-ended queue, then it is conceivable that we could add elements from the left, but this is usually not the case.)
Removing elements: Adding values generally happens from the right. Removal of values, which typically precedes the addition of new values, also generally happens from the right. Why? Because values that would otherwise break the invariant are effectively popped from the top/right before adding the new value to the top/right. Consider the following examples that illustrate what elements must be removed to keep the invariant intact in order to accommodate the addition of the value 5:
Strictly decreasing
[12, 10, 9, 5, 3, 2, 1] # Before addition of 5 [12, 10, 9, 5] # After addition of 5
Weakly decreasing
[12, 10, 10, 9, 5, 3, 1, 0] # Before addition of 5 [12, 10, 10, 9, 5, 5] # After addition of 5
Strictly increasing
[0, 1, 3, 5, 6, 10, 11] # Before addition of 5 [0, 1, 3, 5] # After addition of 5
Weakly increasing
[1, 2, 2, 3, 5, 7, 8, 10] # Before addition of 5 [1, 2, 2, 3, 5, 5] # After addition of 5
It's clear visually from above that values are being removed from the right in order to accommodate the addition of the new value 5.
Removing elements from the left (when a queue-like operation is needed): In some cases (e.g., sliding windows), we may want to remove an element in our collection from the left. As illustrated previously, our collection's invariant is maintained with stack-like operations, namely popping old values from the top before pushing a new value to the top. This means values in our collection progress left to right from "oldest" to "newest" in terms of the recency in which each value was added.

For sliding window problems especially, window values are generally added as the right endpoint advances and removed as the left endpoint advances. Since the leftmost values in our collection are always the "oldest", it makes sense that in certain scenarios we might want to remove the leftmost value. For example, suppose we have the strictly increasing collection [2, 4, 6] that represents the values of the following sliding window:
```
12, 4, [2, 4, 7, 6], 8, 10
```
What happens to our collection once the left boundary of the window advances? It's clear that 2 is no longer a valid value, and we must remove it from our collection.

But stacks are not optimized for removing elements from the left. This is why double-ended queues (i.e., deques) are needed for some problems: the right end permits the stack-like push and pop operations for maintaining the (weakly) increasing/decreasing monotonicity invariant while the left end permits the queue-like operation of popping elements from the left. Note that the invariant is always left intact when elements are removed.

Next larger/smaller (or equal) value: See again the examples above for what elements must be removed in order to accommodate the addition of the 5 and what this means for each removed element's next larger or smaller value (first recall that elements in the collection progress left to right from "oldest" to "newest" in terms of the recency in which they were added to the collection):

Monotonic invariant for collection	Added `5`'s relation to removed elements	Explanation
Strictly decreasing	Larger than or equal	The original value collection `[12, 10, 9, 5, 3, 2, 1]` is transformed to `[12, 10, 9]` before the addition of `5`; hence, the following values are removed (in this order): `1`, `2`, `3`, `5`. Each value removed is less than or equal to the newly added value of `5`. This means that the removed values `1`, `2`, `3`, `5` all have `5` as their next "larger than or equal" value.
Weakly decreasing	Larger than	The original value collection `[12, 10, 10, 9, 5, 3, 1, 0]` is transformed to `[12, 10, 10, 9, 5]` before the addition of `5`; hence, the following values are removed (in this order): `0`, `1`, `3`. Each value removed is less than the newly added value of `5`. This means that the removed values `0`, `1`, `3` all have `5` as their next "larger than" value.
Strictly increasing	Smaller than or equal	The original value collection `[0, 1, 3, 5, 6, 10, 11]` is transformed to `[0, 1, 3]` before the addition of `5`; hence, the following values are removed (in this order): `11`, `10`, `6`, `5`. Each value removed is greater than or equal to the newly added value of `5`. This means that the removed values `11`, `10`, `6`, `5` all have `5` as their next "smaller than or equal" value.
Weakly increasing	Smaller than	The original value collection `[1, 2, 2, 3, 5, 7, 8, 10]` is transformed to `[1, 2, 2, 3, 5]` before the addition of `5`; hence, the following values are removed (in this order): `10`, `8`, `7`. Each value removed is greater than the newly added value of `5`. This means that the removed values `10`, `8`, `7` all have `5` as their next "smaller than" value.

As all of the examples above indicate, if B is the value being added to the collection, then every value A popped from the collection has B as their next "larger/smaller (or equal)" value, where the larger/smaller (or equal) determination completely depends on what kind of monotonic invariant is being maintained for the collection.

Furthermore, once every element in an input array has been iterated over, all remaining elements in the collection are those which had no such next larger/smaller (or equal) value based on the monotonic invariant being maintained for the collection. For example, if strictly increasing is the monotonic invariant being maintained, then, once the input array has been fully iterated over, all remaining elements in the collection have no next "smaller than or equal" value.

Previous larger/smaller (or equal) value: This is a bit harder to conceptualize at first, but it's worth it. In the "next larger/smaller (or equal) value" bullet point above, we were effectively trying to determine how 5 related to each element removed from the collection; that is, the value 5 was each removed element's "next larger/smaller (or equal)" value.

If, however, we think about what happens when we stop removing elements, then we have actually obtained some useful information about a value previous to the 5 that we're trying to add to the collection. Since our collection holds values from "oldest" to "newest" (left to right), once we stop removing elements from the collection, the rightmost element still in the collection is actually 5's "previous larger/smaller (or equal)" value, where the larger/smaller (or equal) determination again depends on what kind of monotonic invariant is being maintained for the collection. If the collection happens to be empty once we stop removing elements before adding 5, then 5 has no "previous larger/smaller (or equal)" value. A table of examples will aid a great deal in clarification:

Monotonic invariant for collection	Relation of rightmost element still in collection to added `5`	Explanation
Strictly decreasing	Previous larger	The original value collection `[12, 10, 9, 5, 3, 2, 1]` is transformed to `[12, 10, 9]` before the addition of `5`. The rightmost value still in the collection is `9`. This means that `9` is `5`'s "previous larger" value.
Weakly decreasing	Previous larger or equal	The original value collection `[12, 10, 10, 9, 5, 3, 1, 0]` is transformed to `[12, 10, 10, 9, 5]` before the addition of `5`. The rightmost value still in the collection is `5`. This means that `5` is `5`'s "previous larger or equal" value.
Strictly increasing	Previous smaller	The original value collection `[0, 1, 3, 5, 6, 10, 11]` is transformed to `[0, 1, 3]` before the addition of `5`. The rightmost value still in the collection is `3`. This means that `3` is `5`'s "previous smaller" value.
Weakly increasing	Previous smaller or equal	The original value collection `[1, 2, 2, 3, 5, 7, 8, 10]` is transformed to `[1, 2, 2, 3, 5]` before the addition of `5`. The rightmost value still in the collection is `5`. This means that `5` is `5`'s "previous smaller or equal" value.

As all of the examples above indicate, if A is the value being added to the collection, then the rightmost value B still in the collection after all removals have taken place (if it exists) is A's "previous larger/smaller (or equal)" value, where the larger/smaller (or equal) determination completely depends on what kind of monotonic invariant is being maintained for the collection (there is no such previous value for A if all elements of the collection have been removed before adding A).

For example, suppose we're given the following array of numbers (indexes drawn above array values for the sake of clarity):

         0  1  2  3  4  5  6  7  8   9
nums = [ 8, 4, 5, 5, 6, 9, 9, 7, 10, 3 ]

If we are maintaining a monotonic collection that is weakly decreasing, then our collection will be [8, 6] by the time we reach index 5. Since our collection is weakly decreasing, we must remove both of the elements currently in the collection before we can add the 9. Thus, there is no rightmost value in the collection once we remove these elements before adding the 9. This means that the 9 at index 5 has no "previous larger or equal" value.

What happens for the value at the next index? The value at index 6 is 9. Since our collection is weakly decreasing, and our current collection is [9], this means we do not need to remove any elements to maintain the monotonic invariant. The rightmost element in the collection before adding the current element is 9, and this means that the 9 at index 6 has 9 as its "previous larger or equal" value. Our collection then becomes [9, 9] once we add the current value of 9.
For the value of 7 at index 7, we do not need to remove any elements from the collection. The current collection's rightmost element is 9, which means the 7 at index 7 has 9 as its "previous larger or equal" value. Add 7 to the collection, which gives us [9, 9, 7] as the current collection.
For the value of 10 at index 8, we must remove all elements of the collection before we can add the 10, which means the 10 at index 8 has no "previous larger or equal" value.

And so on. For each number encountered, we immediately determine that number's "previous value" by first popping all elements from the collection that would break the collection's monotonic invariant. The rightmost element remaining in the collection, if there is one, is the current element's "previous value"; otherwise, if the collection is empty, the current element has no such "previous value", as demonstrated above.

Previous AND next larger/smaller (or equal) values: Take a closer look at the tables from the two bullet points above. Note how "next" and "previous" values are obtained in relation to the current element we're about to add to the collection:

Next values: Each value removed from the collection has the current element we're trying to add to the collection as its next larger/smaller (or equal) value.
Previous values: We cannot add the current element to the collection until all values have been removed from the collection that would otherwise cause the collection's monotonic invariant to be broken with the addition of the current element.

Once the removals from the collection have taken place, and before adding the current element to the collection, we note that the current element's previous larger/smaller (or equal) value is the rightmost value remaining in the collection (if there is one). If no values remain in the collection after the removals above, then the current element has no previous larger/smaller (or equal) value.

The key observation is that both "next" and "previous" value determinations above can be made while processing the same element; that is, "next" values are determined first while elements are being removed from the collection, and then the current element's "previous" value is determined second by checking whether or not the collection still has any values, specifically the rightmost value, after all the removals. These determinations are made in sequence before adding the current element to the collection.

The takeaway is that we get both pieces of information above without any extra computational work. Determining each element's "next" value in some comparative capacity is often how monotonic stacks are used to solve various problems, but what we've noticed above is that, if it's relevant to solving the given problem, then we can also obtain information about each element's "previous" value at no extra cost. The following table, which combines the examples from the previous two tables, makes all of this more concrete:

Monotonic invariant	NEXT value relation of removed elements to added element	PREVIOUS value relation to added element	Explanation
Strictly decreasing	Larger than or equal	Larger than	The original value collection `[12, 10, 9, 5, 3, 2, 1]` is transformed to `[12, 10, 9]` before the addition of `5`; hence, the following values are removed (in this order): `1`, `2`, `3`, `5`. Each value removed is smaller than or equal to the newly added value of `5`. This means that the removed values `1`, `2`, `3`, `5` all have `5` as their next "larger than or equal" value. Before adding `5` to the updated collection `[12, 10, 9]`, note that the collection's rightmost element is `9`, which means `9` is `5`'s previous "larger than" value. We finally add `5` to the collection.
Weakly decreasing	Larger than	Larger than or equal	The original value collection `[12, 10, 10, 9, 5, 3, 1, 0]` is transformed to `[12, 10, 10, 9, 5]` before the addition of `5`; hence, the following values are removed (in this order): `0`, `1`, `3`. Each value removed is smaller than the newly added value of `5`. This means that the removed values `0`, `1`, `3` all have `5` as their next "larger than" value. Before adding `5` to the updated collection `[12, 10, 10, 9, 5]`, note that the collection's rightmost element is `5`, which means `5` is `5`'s previous "larger than or equal" value. We finally add `5` to the collection.
Strictly increasing	Smaller than or equal	Smaller than	The original value collection `[0, 1, 3, 5, 6, 10, 11]` is transformed to `[0, 1, 3]` before the addition of `5`; hence, the following values are removed (in this order): `11`, `10`, `6`, `5`. Each value removed is larger than or equal to the newly added value of `5`. This means that the removed values `11`, `10`, `6`, `5` all have `5` as their next "smaller than or equal" value. Before adding `5` to the updated collection `[0, 1, 3]`, note that the collection's rightmost element is `3`, which means `3` is `5`'s previous "smaller than" value. We finally add `5` to the collection.
Weakly increasing	Smaller than	Smaller than or equal	The original value collection `[1, 2, 2, 3, 5, 7, 8, 10]` is transformed to `[1, 2, 2, 3, 5]` before the addition of `5`; hence, the following values are removed (in this order): `10`, `8`, `7`. Each value removed is larger than the newly added value of `5`. This means that the removed values `10`, `8`, `7` all have 5 as their next "smaller than" value. Before adding `5` to the updated collection `[1, 2, 2, 3, 5]`, note that the collection's rightmost element is `5`, which means `5` is `5`'s previous "smaller than or equal" value. We finally add `5` to the collection.

The table above hints at the fact that, after only a single pass, we can completely process an array of numbers to determine the following depending on which monotonic invariant is being maintained for our collection:

(strictly decreasing) each number's previous larger value as well as its next larger than or equal value

This effectively allows us to determine over what range of values the current number can be considered a maximum (just exclude the number's previous larger value as well as its next larger than or equal value from the range — then the current number must be the largest value in the range).
(weakly decreasing) each number's previous larger or equal value as well as its next larger value

This also effectively allows us to determine over what range of values the current number can be considered a maximum (just exclude the number's previous larger or equal value as well as its next larger value from the range — then the current number must be the largest value in the range).
(strictly increasing) each number's previous smaller value as well as its next smaller than or equal value

This effectively allows us to determine over what range of values the current number can be considered a minimum (just exclude the number's previous smaller value as well as its next smaller than or equal value from the range — then the current number must be the smallest value in the range).
(weakly increasing) each number's previous smaller or equal value as well as its next smaller value

This also effectively allows us to determine over what range of values the current number can be considered a minimum (just exclude the number's previous smaller or equal value as well as its next smaller value from the range — then the current number must be the smallest value in the range).

The insights from the bulleted points above are largely responsible for how we can come up with the optimal solutions to LC 907. Sum of Subarray Minimums and LC 2104. Sum of Subarray Ranges, two problems that would otherwise be exceedingly difficult to solve efficiently. These problems are remarked on in great detail in this post's epilogue, but solutions directly based on the comments above are included as "Approach 2" for each problem in the solved practice problems section.

Monotonic stack definition

Observations are much more important than definitions

The important observations discussed previously are far more important than the simple definitions that follow.

A monotonic stack is a stack whose values demonstrate monotonicity in some capacity: strictly decreasing, weakly decreasing, strictly increasing, or weakly increasing. The following are all examples of monotonic stacks (with an illustration of how monotonicity is maintained when a new value, 5, is added):

Monotonic stack (strictly decreasing)
[12, 10, 9, 5, 3, 2, 1] # Before addition of 5
[12, 10, 9, 5]          # After addition of 5

Monotonic stack (weakly decreasing)
[12, 10, 10, 9, 5, 3, 1, 0] # Before addition of 5
[12, 10, 10, 9, 5, 5]       # After addition of 5

Monotonic stack (strictly increasing)
[0, 1, 3, 5, 6, 10, 11] # Before addition of 5
[0, 1, 3, 5]            # After addition of 5

Monotonic stack (weakly increasing)
[1, 2, 2, 3, 5, 7, 8, 10] # Before addition of 5
[1, 2, 2, 3, 5, 5]        # After addition of 5

What defines the stack, however, is its interface, namely pushing and popping values from the right.

Monotonic queue (deque) definition

Observations are much more important than definitions

The important observations discussed previously are far more important than the simple definitions that follow.

A monotonic queue is really a double-ended queue or deque whose values demonstrate monotonicity in some capacity: strictly decreasing, weakly decreasing, strictly increasing, or weakly increasing. The following are all examples of monotonic deques (with an illustration of how monotonicity is maintained when a new value, 5, is added):

Monotonic deque (strictly decreasing)
[12, 10, 9, 5, 3, 2, 1] # Before addition of 5
[12, 10, 9, 5]          # After addition of 5

Monotonic deque (weakly decreasing)
[12, 10, 10, 9, 5, 3, 1, 0] # Before addition of 5
[12, 10, 10, 9, 5, 5]       # After addition of 5

Monotonic deque (strictly increasing)
[0, 1, 3, 5, 6, 10, 11] # Before addition of 5
[0, 1, 3, 5]            # After addition of 5

Monotonic deque (weakly increasing)
[1, 2, 2, 3, 5, 7, 8, 10] # Before addition of 5
[1, 2, 2, 3, 5, 5]        # After addition of 5

What defines the queue, however, is its interface, namely pushing new elements to the right and popping old elements from the left. The illustrations above clearly show collections of values where all old values are popped from the right, not from the left. This means the popping and pushing of values illustrated above are fundamentally stack-like in nature.

This is why the label of "monotonic queue" is a misnomer — it's misleading. We only claim to use a monotonic queue when removing elements from the left is necessary. In such cases, we use a double-ended queue or deque because the right end still needs the stack-like operations to maintain the invariant while the left end needs the queue-like operation of efficiently removing an element(s) from the left. Hence, it would be more accurate to call a monotonic queue a monotonic deque.

Common use cases for monotonic stacks and deques

Monotonic stacks and deques can crop up in unexpected ways and places, but the following are some conventional areas where these structures shine:

efficiently adding or removing values to a sorted collection of values while maintaining the sorted order
efficiently accessing a value's next larger/smaller (or equal) value
efficiently accessing a value's previous larger/smaller (or equal) value
efficiently accessing the maximum or minimum value of a contiguous subarray or sliding window

A simple stack (or list in Python) is sufficient for the first three points above, but a deque is needed for the last point. In general, deques are needed in the following circumstances:

sliding window problems where efficient access to the maximum or minimum is important
there's a bidirectional nature to the problem where values need to be processed in the order they appear and removed when no longer relevant
old values need to be discarded as new values are processed
insertion of new values causes invalidation of previously stored values (the deque allows efficient insertion of new values from the right and efficient removal of invalidated values from the left)

Monotonic deques can be used for more than just contiguous subarray or sliding window problems where access to the maximum or minimum is needed, but these are clearly situations where all of the points above apply and the use of a deque is warranted. Monotonic stacks can be used for everything else when removals from the left are not needed (e.g., next/previous larger/smaller (or equal) value, largest area or volume problems, stock span problems, etc.). A general safe rule of thumb to follow:

Start with a stack and only move to a deque if you realize you need to remove elements from the left for some reason.

The next few sections are devoted to probably two of the most common use cases for monotonic stacks: given an array of values, identify each value's next/previous larger/smaller (or equal) value (or indicate with -1 if it does not exist). The "next" and "previous" value problems can essentially be solved by means of two templates (one for the "next" value problems and one for the "previous" value problems), where only the comparison operator used to maintain the stack invariant dictates what kinds of values we can expect. Also, as alluded to in the important observations section, we can determine "next" and "previous" values in one pass — this approach is also covered below (after considering "next" and "previous" value determinations separately).

Templates for finding an element's "next" or "previous" value based on monotonic invariant being maintained

tip

The templates below will likely be much easier to understand if you first read the following bullet points in the important observations section, respectively:

"Next greater/smaller (or equal) value"
"Previous greater/smaller (or equal) value"
"Previous AND next larger/smaller (or equal) values"

Memorization suggestion

caution

If you're thoroughly familiar with the structure and rationale of the templates below and your while loop conditional for maintaining the stack invariant is always written in the flavor

while stack and nums[stack[-1]] ? curr_val:

where nums[stack[-1]] appears on the left of the comparison nums[stack[-1]] ? curr_val, then the tables below present easy ways to remember what kinds of values you can expect in your answer array based on what kind of comparison is being used to maintain the stack invariant.

NEXT value (flipped phonetic comparison operator):

NEXT values obtained	Phonetic comparsion	Comparison operator for maintaining stack (flipped)
Next larger	`>`	`<`
Next larger or equal to	`>=`	`<=`
Next smaller	`<`	`>`
Next smaller or equal to	`<=`	`>=`

PREVIOUS value (negated phonetic comparison operator):

PREVIOUS values obtained	Phonetic comparsion	Comparison operator for maintaining stack (negated)
Previous larger	`>`	`<=`
Previous larger or equal to	`>=`	`<`
Previous smaller	`<`	`>=`
Previous smaller or equal to	`<=`	`>`

Next value template
def fn_next(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_B = nums[i]
        # the comparison operator (?) dictates what A's next value B represents
        # (<)  next larger value (weakly decreasing stack)
        # (<=) next larger or equal value (strictly decreasing stack)
        # (>)  next smaller value (weakly increasing stack)
        # (>=) next smaller or equal value (strictly increasing stack)
        while stack and nums[stack[-1]] ? val_B:
            idx_val_A = stack.pop()
            ans[idx_val_A] = val_B
        stack.append(i)
    
    # process elements that never had a "next" value that satisfied the criteria
    while stack:
        idx_val_A = stack.pop()
        ans[idx_val_A] = -1
    
    return ans

Previous value template
def fn_previous(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_A = nums[i]
        # the comparison operator (?) dictates what A's previous value B represents
        # (<=) previous larger (strictly decreasing)
        # (<)  previous larger or equal value (weakly decreasing)
        # (>=) previous smaller value (strictly increasing)
        # (>)  previous smaller or equal value (weakly increasing)
        while stack and nums[stack[-1]] ? val_A:
            stack.pop()
            
        if stack:
            idx_val_B = stack[-1]
            val_B = nums[idx_val_B]
            ans[i] = val_B
        else:
            ans[i] = -1
        
        stack.append(i)
        
    return ans

Combined templates for previous and next values
def fn(nums):
    n = len(nums)
    ans = [[-1, -1] for _ in range(n)] # default values for missing PREVIOUS and NEXT values, respectively
    stack = [] # monotonic stack
    
    # the comparison operator (?) dictates what each element's PREVIOUS and NEXT values will be
    # (<=) PREVIOUS larger value and NEXT larger or equal value (strictly decreasing stack)
    # (<)  PREVIOUS larger or equal value and NEXT larger value (weakly decreasing stack)
    # (>=) PREVIOUS smaller value and NEXT smaller or equal value (strictly increasing stack)
    # (>)  PREVIOUS smaller or equal value and NEXT smaller value (weakly increasing stack)
    for i in range(n):
        while stack and nums[stack[-1]] ? nums[i]:
            # NEXT values processed
            idx = stack.pop()
            ans[idx][1] = i # use nums[i] instead of i to directly record array values instead of indexes
        # PREVIOUS values processed
        ans[i][0] = -1 if not stack else stack[-1] # use nums[stack[-1]] instead of stack[-1] 
                                                   # to directly record array values instead of indexes 
        stack.append(i)
    
    return ans

It's most important to become very familiar with the structure of each template above (i.e., why things are structured the way they are). Remembering which comparison operator corresponds to which kind of monotonic stack being maintained, and thus what kind of criteria-satisfying value we're searching for, is much less important: this can easily be attained by providing yourself with a sample stack of values and asking yourself what you would need to do if you tried inserting a new value into the stack (make it concrete by giving yourself a monotonic stack with a few elements and then trying to insert another element). Answering your own question in this way will tell you what kind of comparison needs to be made to find the values you're searching for, but none of this will help unless you know the structure for maintaining the stack.

The following three sections separately consider each problem that leads to each template above.

Common problem (with template): Find a value's "next" larger/smaller (or equal) value

Monotonic stacks below contain index values

Monotonic stacks will very often not contain the input array's values themselves but the indexes which point to these values. This makes it possible for us to not only get access to the array values themselves but also to positional information about where the array values reside. This can be confusing at first though if you are only used to seeing monotonic stacks that directly use array values.

Consult the template and/or tabular summary as reference points

The next value template and/or next value "tabular summary", which appear after the provided solutions/approaches to the questions posed in the bulleted list below, can be quite helpful to use as reference points while working through the various approaches.

One of the most common use cases for a monotonic stack is to determine each value's "next" larger/smaller (or equal) value (i.e., the value that comes to the right of a given value that meets the desired criteria):

Next larger value: Given value A, what is the next value B such that A < B?
Next larger or equal value: Given value A, what is the next value B such that A <= B?
Next smaller value: Given value A, what is the next value B such that A > B?
Next smaller or equal value: Given value A, what is the next value B such that A >= B?

Note that the value B referred to above will always be in reference to the current value being processed since we will be processing the values from left to right (the monotonic stack will always be comprised of previous elements we've encountered, oldest to newest, left to right, whose next value that meets the criteria is the current value we are considering). To illustrate this more clearly, each problem variation in the bulleted list above is solved below where the roles of "values A and B" have been explicitly designated in each solution (i.e., value B always refers to value A's next value that meets the specified criteria).

The following array of numbers will be used as input in each solution approach for the sake of clarity and consistency:

nums = [14, 17, 13, 14, 14, 19, 12, 14, 18]

Values that ultimately end up having no next value that satisfies the specified criteria will report a "next value" of -1 in the answer array to communicate this. The answer array, ans, is always initialized to the length of the input array and filled with None values. This is done to concretely show how every element is processed (i.e., as opposed to initializing the answer array with -1 and then not processing values that never have a next value that satisfies the criteria).

Next larger value

def fn(nums):
    n = len(nums)
    ans = [None] * n
    dec_stack = [] # monotonic stack (weakly decreasing)
    for i in range(n):
        val_B = nums[i]
        while dec_stack and nums[dec_stack[-1]] < val_B:
            idx_val_A = dec_stack.pop()
            ans[idx_val_A] = val_B
        dec_stack.append(i)
    
    # process elements that never had a next larger value
    while dec_stack:
        idx_val_A = dec_stack.pop()
        ans[idx_val_A] = -1
    
    return ans

nums =            [14, 17, 13, 14, 14, 19, 12, 14, 18]
print(fn(nums)) # [17, 19, 14, 19, 19, -1, 14, 18, -1]

Intuition

The current value being processed, val_B, is always the next value in relation to whatever values are in the stack (since the stack is comprised of values encountered before the current value); hence, for another value, val_A, to have val_B as its next larger value, the value val_A will need to be popped from the stack, and it will need to be smaller than (<) the current value, val_B.

Maintaining a weakly decreasing monotonic stack is perfectly suited for solving this problem. To see why, consider what would need to happen if we tried adding 5 to the following stack: [8, 6, 5, 4, 4].

Is 4 less than 5? Yes. Pop 4 from the stack, and note that 4's next larger value is 5. Stack's new state: [8, 6, 5, 4].
Is 4 less than 5? Yes. Pop 4 from the stack, and note that 4's next larger value is 5. Stack's new state: [8, 6, 5].
Is 5 less than 5? No. Push 5 to the stack. Stack's new state: [8, 6, 5, 5]. Continue to next element.

This is how each "next larger value" is determined.

Next larger or equal value

def fn(nums):
    n = len(nums)
    ans = [None] * n
    dec_stack = [] # monotonic stack (strictly decreasing)
    for i in range(n):
        val_B = nums[i]
        while dec_stack and nums[dec_stack[-1]] <= val_B:
            idx_val_A = dec_stack.pop()
            ans[idx_val_A] = val_B
        dec_stack.append(i)
    
    # process elements that never had a next larger or equal value
    while dec_stack:
        idx_val_A = dec_stack.pop()
        ans[idx_val_A] = -1
    
    return ans

nums =            [14, 17, 13, 14, 14, 19, 12, 14, 18]
print(fn(nums)) # [17, 19, 14, 14, 19, -1, 14, 18, -1]

Intuition

The current value being processed, val_B, is always the next value in relation to whatever values are in the stack (since the stack is comprised of values encountered before the current value); hence, for another value, val_A, to have val_B as its next larger or equal value, the value val_A will need to be popped from the stack, and it will need to be smaller than or equal (<=) to the current value, val_B.

Maintaining a strictly decreasing monotonic stack is perfectly suited for solving this problem. To see why, consider what would need to happen if we tried adding 5 to the following stack: [8, 6, 5, 4].

Is 4 less than or equal to 5? Yes. Pop 4 from the stack, and note that 4's next larger or equal value is 5. Stack's new state: [8, 6, 5].
Is 5 less than or equal to 5? Yes. Pop 5 from the stack, and note that 5's next larger or equal value is 5. Stack's new state: [8, 6].
Is 6 less than or equal to 5? No. Push 5 to the stack. Stack's new state: [8, 6, 5]. Continue to next element.

This is how each "next larger or equal value" is determined.

Next smaller value

def fn(nums):
    n = len(nums)
    ans = [None] * n
    inc_stack = [] # monotonic stack (weakly increasing)
    for i in range(n):
        val_B = nums[i]
        while inc_stack and nums[inc_stack[-1]] > val_B:
            idx_val_A = inc_stack.pop()
            ans[idx_val_A] = val_B
        inc_stack.append(i)
    
    # process elements that never had a next smaller value
    while inc_stack:
        idx_val_A = inc_stack.pop()
        ans[idx_val_A] = -1
    
    return ans

nums =            [14, 17, 13, 14, 14, 19, 12, 14, 18]
print(fn(nums)) # [13, 13, 12, 12, 12, 12, -1, -1, -1]

Intuition

The current value being processed, val_B, is always the next value in relation to whatever values are in the stack (since the stack is comprised of values encountered before the current value); hence, for another value, val_A, to have val_B as its next smaller value, the value val_A will need to be popped from the stack, and it will need to be larger than (>) the current value, val_B.

Maintaining a weakly increasing monotonic stack is perfectly suited for solving this problem. To see why, consider what would need to happen if we tried adding 8 to the following stack: [3, 4, 8, 9, 9].

Is 9 greater than 8? Yes. Pop 9 from the stack, and note that 9's next smaller value is 8. Stack's new state: [3, 4, 8, 9].
Is 9 greater than 8? Yes. Pop 9 from the stack, and note that 9's next smaller value is 8. Stack's new state: [3, 4, 8].
Is 8 less than 8? No. Push 8 to the stack. Stack's new state: [3, 4, 8, 8]. Continue to next element.

This is how each "next smaller value" is determined.

Next smaller or equal value

def fn(nums):
    n = len(nums)
    ans = [None] * n
    inc_stack = [] # monotonic stack (strictly increasing)
    for i in range(n):
        val_B = nums[i]
        while inc_stack and nums[inc_stack[-1]] >= val_B:
            idx_val_A = inc_stack.pop()
            ans[idx_val_A] = val_B
        inc_stack.append(i)
    
    # process elements that never had a next smaller or equal value
    while inc_stack:
        idx_val_A = inc_stack.pop()
        ans[idx_val_A] = -1
    
    return ans

nums =            [14, 17, 13, 14, 14, 19, 12, 14, 18]
print(fn(nums)) # [13, 13, 12, 14, 12, 12, -1, -1, -1]

Intuition

The current value being processed, val_B, is always the next value in relation to whatever values are in the stack (since the stack is comprised of values encountered before the current value); hence, for another value, val_A, to have val_B as its next smaller or equal value, the value val_A will need to be popped from the stack, and it will need to be larger than or equal (>=) to the current value, val_B.

Maintaining a strictly increasing monotonic stack is perfectly suited for solving this problem. To see why, consider what would need to happen if we tried adding 8 to the following stack: [3, 4, 8, 9].

Is 9 greater than or equal to 8? Yes. Pop 9 from the stack, and note that 9's next smaller or equal value is 8. Stack's new state: [3, 4, 8].
Is 8 greater than or equal to 8? Yes. Pop 8 from the stack, and note that 8's next smaller or equal value is 8. Stack's new state: [3, 4].
Is 4 greater than or equal to 8? No. Push 8 to the stack. Stack's new state: [3, 4, 8]. Continue to next element.

This is how each "next smaller or equal value" is determined.

General template for "next value" problems

All of the approaches above are very similar except largely the kind of monotonic stack used to find elements satisfying the specified criteria. The following is a generalized template that can be slightly tweaked to get the desired result (only the comparison operator ? in the while loop's conditional, nums[stack[-1]] ? val_B, has to be changed):

def fn(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_B = nums[i]
        # the comparison operator (?) dictates what A's next value B represents
        # (<)  next larger value (weakly decreasing stack)
        # (<=) next larger or equal value (strictly decreasing stack)
        # (>)  next smaller value (weakly increasing stack)
        # (>=) next smaller or equal value (strictly increasing stack)
        while stack and nums[stack[-1]] ? val_B:
            idx_val_A = stack.pop()
            ans[idx_val_A] = val_B
        stack.append(i)
    
    # process elements that never had a "next" value that satisfied the criteria
    while stack:
        idx_val_A = stack.pop()
        ans[idx_val_A] = -1
    
    return ans

What happens if we use == or != for value comparison when managing our collection?

caution

It's probably best to skip this for now unless you're fully comfortable with everything that has been previously discussed in this post. The brief considerations we're about to make are likely to cause confusion and will add little to no (maybe negative?) benefit. If you're not yet deterred, then it might possibly be useful to concretely see why using these comparisons adds little value to our analyses.

Using the equality comparison: ==

TLDR: The answer array is only ever updated (i.e., ans[i] = curr_num) when equivalent values are adjacent: if nums[i] == nums[i+1], then the assignment ans[i] = nums[i+1] will be made. But this is the only scenario where updates are made (probably not a desirable nor useful effect).

It's tempting to think we're asking, "What is the next value equal to the current value?" This is somewhat of a ridiculous question since any value will clearly be its own next equal value if this value is ever repeated (the question of whether or not the value is ever repeated is the real question here). If our code actually attempted to answer this question by only changing the comparison operator to ==, then we would expect the following input-output result:

# Input
[14, 17, 13, 14, 14, 19, 12, 14, 18]

# Output
[14, -1, -1, 14, 14, -1, -1, -1, -1]

Let's run the code and see what we get (we'll add a helpful print statement too for clarification):

Input-Output
def fn(nums):
    collection = []
    ans = [-1] * len(nums)
    
    for i in range(len(nums)):
        curr_num = nums[i]
        while collection and nums[collection[-1]] == curr_num:
            prev_index = collection.pop()
            ans[prev_index] = curr_num
        collection.append(i)
        print(
            f'collection: {collection}; '
            f'number correspondence: {[nums[idx] for idx in collection]}'
        )
        
    return ans

nums = [14, 17, 13, 14, 14, 19, 12, 14, 18] # Input
fn(nums)                                    # Output: [-1, -1, -1, 14, -1, -1, -1, -1, -1]

Printed information
Index: 0;  Value: 14  Index collection: [0]                       Collection values: [14];                              Answer array: [-1, -1, -1, -1, -1, -1, -1, -1, -1]
Index: 1;  Value: 17  Index collection: [0, 1]                    Collection values: [14, 17];                          Answer array: [-1, -1, -1, -1, -1, -1, -1, -1, -1]
Index: 2;  Value: 13  Index collection: [0, 1, 2]                 Collection values: [14, 17, 13];                      Answer array: [-1, -1, -1, -1, -1, -1, -1, -1, -1]
Index: 3;  Value: 14  Index collection: [0, 1, 2, 3]              Collection values: [14, 17, 13, 14];                  Answer array: [-1, -1, -1, -1, -1, -1, -1, -1, -1]
Index: 4;  Value: 14  Index collection: [0, 1, 2, 4]              Collection values: [14, 17, 13, 14];                  Answer array: [-1, -1, -1, 14, -1, -1, -1, -1, -1]
Index: 5;  Value: 19  Index collection: [0, 1, 2, 4, 5]           Collection values: [14, 17, 13, 14, 19];              Answer array: [-1, -1, -1, 14, -1, -1, -1, -1, -1]
Index: 6;  Value: 12  Index collection: [0, 1, 2, 4, 5, 6]        Collection values: [14, 17, 13, 14, 19, 12];          Answer array: [-1, -1, -1, 14, -1, -1, -1, -1, -1]
Index: 7;  Value: 14  Index collection: [0, 1, 2, 4, 5, 6, 7]     Collection values: [14, 17, 13, 14, 19, 12, 14];      Answer array: [-1, -1, -1, 14, -1, -1, -1, -1, -1]
Index: 8;  Value: 18  Index collection: [0, 1, 2, 4, 5, 6, 7, 8]  Collection values: [14, 17, 13, 14, 19, 12, 14, 18];  Answer array: [-1, -1, -1, 14, -1, -1, -1, -1, -1]

What's going on here? Why is the answer array only updated once (after the value at index 4 is processed)? The answer isn't obvious at first and even gave ChatGPT 4 quite a few issues (you can ignore the first two messages in the ChatGPT thread). We can answer our own question by looking at the code more closely and determining what changing the comparison to == actually does. Here's the core part of the function:

for i in range(len(nums)):
    curr_num = nums[i]
    while collection and nums[collection[-1]] == curr_num:
        prev_index = collection.pop()
        ans[prev_index] = curr_num
    collection.append(i)

When exactly are values added to collection? Once all previous values that equal the current value have been removed. For example, if the current number is x and the collection before processing this number somehow corresponded to the numbers [a, b, d, c, g, f, x, x, x], then the collection's number correspondence' after processing the current number would be [a, b, d, c, g, f, x], where the three equivalent x values previously in the collection were removed (and their corresponding spots in the answer array updated). This explains the crucial logic in the function above, but we should note that the collection itself will never have adjacent indexes that represent equivalent values due to how the collection is being maintained; that is, to use the example above, we would never actually reach the state of [a, b, d, c, g, f, x, x, x]. We would first reach [a, b, d, c, g, f, x] and the collection would stay this way until we encountered a new value not equal to x.

This may be easier to understand if we introduce an actual number array that models the situation above (the number above each value corresponds to that value's index):

        0  1  2  3  4  5  6   7   8   9
nums = [1, 2, 4, 3, 7, 6, 24, 24, 24, 24]

Eventually our collection of index values reaches the state [0, 1, 2, 3, 4, 5, 6], where nums[6] == 24, and we know the next three values are all 24; that is, nums[6] == nums[7] == nums[8] == nums[9]. How is collection maintained and how is our answer array updated?

Collection: [0, 1, 2, 3, 4, 5, 6]. Current value (index 7): 24. We have nums[6] == nums[7].
- Pop 6
- Update answer array: ans[6] = 24
- Append 7 to the collection
Collection: [0, 1, 2, 3, 4, 5, 7]. Current value (index 8): 24. We have nums[7] == nums[8].
- Pop 7
- Update answer array: ans[7] = 24
- Append 8 to the collection
Collection: [0, 1, 2, 3, 4, 5, 8]. Current value (index 9): 24. We have nums[8] == nums[9].
- Pop 8
- Update answer array: ans[8] = 24
- Append 9 to the collection

This is where we'd stop because we just processed the last value in nums at index 9. Since the answer array is not updated at all until index 6, and is then updated in the manner above, our final answer array would be [-1, -1, -1, -1, -1, 24, 24, 24, -1]. If we execute the fn function above with nums = [1, 2, 4, 3, 7, 6, 24, 24, 24, 24] as the input, then this is exactly what we will get as the output.

For the sake of completeness, here's a way to answer the question we originally thought we might be asking (i.e., what is the next equal value or -1 if no such value exists):

def fn(nums):
    collection = set()
    ans = [None] * len(nums)
    for i in range(len(nums) - 1, -1, -1):
        curr_num = nums[i]
        if curr_num in collection:
            ans[i] = curr_num
        else:
            ans[i] = -1
            collection.add(curr_num)
    return ans

nums =     [14, 17, 13, 14, 14, 19, 12, 14, 18]
fn(nums) # [14, -1, -1, 14, 14, -1, -1, -1, -1]

Using the inequality comparison: !=

TLDR: The answer array is updated whenever unequal values are adjacent. If two or more adjacent values are equal, then the indexes that represent these values are all added to the index collection, and the answer array is not updated until an unequal value is found, at which point all previous equal adjacent values are assigned this current unequal value in the answer array.

Due to the last in first out nature of how values are being maintained in the index collection, the effect of changing the comparison operator to != is that the answer array effectively tells us what each value's next unequal value will be (or -1 if no such value exists). This isn't entirely worthless, but it is also probably not the most desired effect nor all that useful a result.

If we change the comparison operator to !=, then it seems like we may be asking the following question: "What is the next value not equal to the current value?" And we'd be right (unlike before with ==) even though the result is unlikely to be all that useful! If we change the comparison operator to !=, then we would expect our code to produce the following input-output result:

# Input
[14, 17, 13, 14, 14, 19, 12, 14, 18]

# Output
[17, 13, 14, 19, 19, 12, 14, 18, -1]

Let's run the code and see what we get (we'll again add a helpful print statement for clarification):

Input-Output
def fn(nums):
    collection = []
    ans = [-1] * len(nums)
    
    for i in range(len(nums)):
        curr_num = nums[i]
        while collection and nums[collection[-1]] != curr_num:
            prev_index = collection.pop()
            ans[prev_index] = curr_num
        collection.append(i)
        print(
            f'Index: {i}; ',
            f'Value: {nums[i]}',
            f'Index collection: {collection}',
            f'Collection values: {[nums[idx] for idx in collection]}; ',
            f'Answer array: {ans}'
        )
        
    return ans

nums = [14, 17, 13, 14, 14, 19, 12, 14, 18] # Input
fn(nums)                                    # Output: [17, 13, 14, 19, 19, 12, 14, 18, -1]

Printed information
Index: 0;  Value: 14  Index collection: [0]     Collection values: [14];      Answer array: [-1, -1, -1, -1, -1, -1, -1, -1, -1]
Index: 1;  Value: 17  Index collection: [1]     Collection values: [17];      Answer array: [17, -1, -1, -1, -1, -1, -1, -1, -1]
Index: 2;  Value: 13  Index collection: [2]     Collection values: [13];      Answer array: [17, 13, -1, -1, -1, -1, -1, -1, -1]
Index: 3;  Value: 14  Index collection: [3]     Collection values: [14];      Answer array: [17, 13, 14, -1, -1, -1, -1, -1, -1]
Index: 4;  Value: 14  Index collection: [3, 4]  Collection values: [14, 14];  Answer array: [17, 13, 14, -1, -1, -1, -1, -1, -1]
Index: 5;  Value: 19  Index collection: [5]     Collection values: [19];      Answer array: [17, 13, 14, 19, 19, -1, -1, -1, -1]
Index: 6;  Value: 12  Index collection: [6]     Collection values: [12];      Answer array: [17, 13, 14, 19, 19, 12, -1, -1, -1]
Index: 7;  Value: 14  Index collection: [7]     Collection values: [14];      Answer array: [17, 13, 14, 19, 19, 12, 14, -1, -1]
Index: 8;  Value: 18  Index collection: [8]     Collection values: [18];      Answer array: [17, 13, 14, 19, 19, 12, 14, 18, -1]

This is nice because we're actually getting the expected behavior here! But why though? Let's take a closer look at the core part of the function where the comparison operator for maintaining our index collection is now !=:

for i in range(len(nums)):
    curr_num = nums[i]
    while collection and nums[collection[-1]] != curr_num:
        prev_index = collection.pop()
        ans[prev_index] = curr_num
    collection.append(i)

This effectively means the answer array gets updated every time we encounter a value not equal to the value represented at the top of the collection. But if the values are equal, as is the case above when the values of 14 are adjacent, then the answer array is not updated, and we wait until the next unequal value is encountered, at which point all previous adjacent values that are equivalent will be popped from the collection and assigned the current uneqal value in the answer array. This is actually the desired effect (even though it doesn't seem particularly useful).

Tabular summary

The tabular summary below compactly describes the examples used to illustrate the approaches in each solution above.

NEXT criteria	comparison	monotonic stack type	example stack	current value	description
next larger value	`<`	weakly decreasing	`[8, 6, 5, 4, 4]`	`5`	The current value of `5` serves as the next larger value for both `4`'s on the stack, which are popped in order to make room for the `5`, resulting in the following new weakly decreasing monotonic stack: `[8, 6, 5, 5]`.
next larger or equal value	`<=`	strictly decreasing	`[8, 6, 5, 4]`	`5`	The current value of `5` serves as the next larger or equal value for the `4` and `5` currently on the stack, which are popped in order to make room for the `5`, resulting in the following new strictly decreasing monotonic stack: `[8, 6, 5]`.
next smaller value	`>`	weakly increasing	`[3, 4, 8, 9, 9]`	`8`	The current value of `8` serves as the next smaller value for both `9`'s on the stack, which are popped in order to make room for the `8`, resulting in the following new weakly increasing monotonic stack: `[3, 4, 8, 8]`.
next smaller or equal value	`>=`	strictly increasing	`[3, 4, 8, 9]`	`8`	The current value of `8` serves as the next smaller or equal value for the `9` and `8` currently on the stack, which are popped in order to make room for the `8`, resulting in the following new strictly increasing monotonic stack: `[3, 4, 8]`.

Common problem (with template): Find a value's "previous" larger/smaller (or equal) value

Monotonic stacks below contain index values

Consult the template and/or tabular summary as reference points

The previous value template and/or previous value "tabular summary", which appear after the provided solutions/approaches to the questions posed in the bulleted list below, can be quite helpful to use as reference points while working through the various approaches.

Another common use case for a monotonic stack (although not as common as the ones immediately above) is to determine each value's "previous" larger/smaller (or equal) value (i.e., the value that comes to the left of a given value that meets the desired criteria):

Previous larger value: Given value A, what is the previous value B such that A < B?
Previous larger or equal value: Given value A, what is the previous value B such that A <= B?
Previous smaller value: Given value A, what is the previous value B such that A > B?
Previous smaller or equal value: Given value A, what is the previous value B such that A >= B?

Note that the value A referred to above will always be in reference to the current value being processed (i.e., the element we're about to add to the stack). Its previous value, which satisfies some criteria, must be in the monotonic stack (since the monotonic stack is always comprised of previous elements we've encountered, oldest to newest, left to right). The idea is to keep popping elements from the monotonic stack that do not meet our desired criteria until either the stack is empty (no previous value meeting the criteria was found) or the last element in the stack does satisfy the criteria, in which case it will be value A's previous value that meets the criteria. To illustrate this more clearly, each problem variation in the bulleted list above is solved below where the roles of "values A and B" have been explicitly designated in each solution (i.e., value B always refers to value A's previous value that meets the specified criteria).

The following array of numbers will be used as input in each solution approach for the sake of clarity and consistency:

nums = [14, 17, 13, 14, 14, 19, 12, 14, 18]

Values that ultimately end up having no previous value that satisfies the specified criteria will report a "previous value" of -1 in the answer array to communicate this. The answer array, ans, is always initialized to the length of the input array and filled with None values. This is done to concretely show how every element is processed.

Previous larger value

def fn(nums):
    n = len(nums)
    ans = [None] * n
    dec_stack = [] # monotonic stack (strictly decreasing)
    for i in range(n):
        val_A = nums[i]
        while dec_stack and nums[dec_stack[-1]] <= val_A:
            dec_stack.pop()
        
        if dec_stack:
            idx_val_B = dec_stack[-1]
            val_B = nums[idx_val_B]
            ans[i] = val_B
        else:
            ans[i] = -1
        
        dec_stack.append(i)
        
    return ans

nums =            [14, 17, 13, 14, 14, 19, 12, 14, 18]
print(fn(nums)) # [-1, -1, 17, 17, 17, -1, 19, 19, 19]

Intuition

The current value being processed, val_A, is always looking for its criteria-satisfying previous value from the stack (since the stack is comprised of values encountered previously to the current value). All previously encountered values that do not satisfy the specified criteria should be removed from the stack. There are two possibilities once such removals are made: either the stack is empty, in which case val_A has no criteria-satisfying previous value, or the stack is not empty, in which case the element on the top of the stack, val_B, is val_A's previous value that satisfies the specified criteria.

For this problem, if the current value, val_A, has a previous larger value, val_B, then val_B must reside in the stack. To access this value, we remove all elements from the stack that are smaller than or equal (<=) to val_A, ensuring the next value on top of the stack (if it exists) is larger than val_A, which is what we want. If the stack is empty after removing all values smaller than or equal to val_A, then there cannot be a previous value, val_B, such that val_B > val_A. If, however, the stack is not empty after removing all values smaller than or equal to val_A, then whatever element resides at the top of the stack is val_B, where val_B > val_A.

Is 4 less than or equal to 5? Yes. Pop 4 from the stack. Stack's new state: [8, 6, 5].
Is 5 less than or equal to 5? Yes. Pop 5 from the stack. Stack's new state: [8, 6].
Is 6 less than or equal to 5? No. Since the stack is not empty, 6 must be 5's previous larger value. Push 5 to the stack. Stack's new state: [8, 6, 5]. Continue to next element.

This is how each "previous larger value" is determined.

Previous larger or equal value

def fn(nums):
    n = len(nums)
    ans = [None] * n
    dec_stack = [] # monotonic stack (weakly decreasing)
    for i in range(n):
        val_A = nums[i]
        while dec_stack and nums[dec_stack[-1]] < val_A:
            dec_stack.pop()
            
        if dec_stack:
            idx_val_B = dec_stack[-1]
            val_B = nums[idx_val_B]
            ans[i] = val_B
        else:
            ans[i] = -1
        
        dec_stack.append(i)
        
    return ans

nums =            [14, 17, 13, 14, 14, 19, 12, 14, 18]
print(fn(nums)) # [-1, -1, 17, 17, 14, -1, 19, 19, 19]

Intuition

For this problem, if the current value, val_A, has a previous larger or equal value, val_B, then val_B must reside in the stack. To access this value, we remove all elements from the stack that are smaller (<) than val_A, ensuring the next value on top of the stack (if it exists) is larger than or equal to val_A, which is what we want. If the stack is empty after removing all values smaller than val_A, then there cannot be a previous value, val_B, such that val_B >= val_A. If, however, the stack is not empty after removing all values smaller than or equal to val_A, then whatever element resides at the top of the stack is val_B, where val_B >= val_A.

Is 4 less than 5? Yes. Pop 4 from the stack. Stack's new state: [8, 6, 5, 4].
Is 4 less than 5? Yes. Pop 4 from the stack. Stack's new state: [8, 6, 5].
Is 5 less than 5? No. Since the stack is not empty, 5 must be 5's previous larger or equal value. Push 5 to the stack. Stack's new state: [8, 6, 5, 5]. Continue to next element.

This is how each "previous larger or equal value" is determined.

Previous smaller value

def fn(nums):
    n = len(nums)
    ans = [None] * n
    inc_stack = [] # monotonic stack (strictly increasing)
    for i in range(n):
        val_A = nums[i]
        while inc_stack and nums[inc_stack[-1]] >= val_A:
            inc_stack.pop()
            
        if inc_stack:
            idx_val_B = inc_stack[-1]
            val_B = nums[idx_val_B]
            ans[i] = val_B
        else:
            ans[i] = -1
        
        inc_stack.append(i)
        
    return ans

nums =            [14, 17, 13, 14, 14, 19, 12, 14, 18]
print(fn(nums)) # [-1, 14, -1, 13, 13, 14, -1, 12, 14]

Intuition

For this problem, if the current value, val_A, has a previous smaller value, val_B, then val_B must reside in the stack. To access this value, we remove all elements from the stack that are larger than or equal (>=) to val_A, ensuring the next value on top of the stack (if it exists) is smaller than val_A, which is what we want. If the stack is empty after removing all values larger than or equal to val_A, then there cannot be a previous value, val_B, such that val_B < val_A. If, however, the stack is not empty after removing all values larger than or equal to val_A, then whatever element resides at the top of the stack is val_B, where val_B < val_A.

Maintaining a strictly increasing monotonic stack is perfectly suited for solving this problem. To see why, consider what would need to happen if we tried adding 5 to the following stack: [4, 5, 6, 8].

Is 8 greater than or equal to 5? Yes. Pop 8 from the stack. Stack's new state: [4, 5, 6].
Is 6 greater than or equal to 5? Yes. Pop 6 from the stack. Stack's new state: [4, 5].
Is 5 greater than or equal to 5? Yes. Pop 5 from the stack. Stack's new state: [4].
Is 4 greater than or equal to 5? No. Since the stack is not empty, 4 must be 5's previous smaller value. Push 5 to the stack. Stack's new state: [4, 5]. Continue to next element.

This is how each "previous smaller value" is determined.

Previous smaller or equal value

def fn(nums):
    n = len(nums)
    ans = [None] * n
    inc_stack = [] # monotonic stack (weakly increasing)
    for i in range(n):
        val_A = nums[i]
        while inc_stack and nums[inc_stack[-1]] > val_A:
            inc_stack.pop()
            
        if inc_stack:
            idx_val_B = inc_stack[-1]
            val_B = nums[idx_val_B]
            ans[i] = val_B
        else:
            ans[i] = -1
        
        inc_stack.append(i)
        
    return ans

nums =            [14, 17, 13, 14, 14, 19, 12, 14, 18]
print(fn(nums)) # [-1, 14, -1, 13, 14, 14, -1, 12, 14]

Intuition

For this problem, if the current value, val_A, has a previous smaller or equal value, val_B, then val_B must reside in the stack. To access this value, we remove all elements from the stack that are larger (>) than val_A, ensuring the next value on top of the stack (if it exists) is smaller than or equal to val_A, which is what we want. If the stack is empty after removing all values larger than val_A, then there cannot be a previous value, val_B, such that val_B <= val_A. If, however, the stack is not empty after removing all values larger than val_A, then whatever element resides at the top of the stack is val_B, where val_B <= val_A.

Maintaining a weakly increasing monotonic stack is perfectly suited for solving this problem. To see why, consider what would need to happen if we tried adding 5 to the following stack: [4, 5, 8, 8].

Is 8 greater than 5? Yes. Pop 8 from the stack. Stack's new state: [4, 5, 8].
Is 8 greater than 5? Yes. Pop 8 from the stack. Stack's new state: [4, 5].
Is 5 greater than 5? No. Since the stack is not empty, 5 must be 5's previous smaller or equal value. Push 5 to the stack. Stack's new state: [4, 5, 5]. Continue to next element.

This is how each "previous smaller or equal value" is determined.

General template for "previous value" problems

def fn(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_A = nums[i]
        # the comparison operator (?) dictates what A's previous value B represents
        # (<=) previous larger (strictly decreasing)
        # (<)  previous larger or equal value (weakly decreasing)
        # (>=) previous smaller value (strictly increasing)
        # (>)  previous smaller or equal value (weakly increasing)
        while stack and nums[stack[-1]] ? val_A:
            stack.pop()
            
        if stack:
            idx_val_B = stack[-1]
            val_B = nums[idx_val_B]
            ans[i] = val_B
        else:
            ans[i] = -1
        
        stack.append(i)
        
    return ans

Tabular summary

The tabular summary below compactly describes the examples used to illustrate the approaches in each solution above.

PREVIOUS criteria	comparison	monotonic stack type	example stack	current value	description
previous larger value	`<=`	strictly decreasing	`[8, 6, 5, 4]`	`5`	The previously encountered values of `4` and `5` are popped off the stack, respectively. Since the stack is now `[8, 6]`, this means the previous larger value for `5` is `6`, the element now on top of the stack (if the stack were empty after the removals, then `5` would have no previous larger value). We now add `5` to the stack and continue processing elements: `[8, 6, 5]`.
previous larger or equal value	`<`	weakly decreasing	`[8, 6, 5, 4, 4]`	`5`	The previously encountered values of `4` and `4` are popped off the stack, respectively. Since the stack is now `[8, 6, 5]`, this means the previous larger value for `5` is `5`, the element now on top of the stack (if the stack were empty after the removals, then `5` would have no previous larger value). We now add `5` to the stack and continue processing elements: `[8, 6, 5, 5]`.
previous smaller value	`>=`	strictly increasing	`[4, 5, 6, 8]`	`5`	The previously encountered values of `8`, `6`, and `5` are popped off the stack, respectively. Since the stack is now `[4]`, this means the previous smaller value for `5` is `4`, the element now on top of the stack (if the stack were empty after the removals, then `5` would have no previous smaller value). We now add `4` to the stack and continue processing elements: `[4, 5]`.
previous smaller or equal value	`>`	weakly increasing	`[4, 5, 8, 8]`	`5`	The previously encountered values of `8` and `8` are popped off the stack, respectively. Since the stack is now `[4, 5]`, this means the previous smaller value for `5` is `4`, the element now on top of the stack (if the stack were empty after the removals, then `5` would have no previous smaller value). We now add `4` to the stack and continue processing elements: `[4, 5]`.

Common problems combined: In one pass, find each value's "next" AND "previous" value based on monotonic invariant

The last bullet point in the important observations section (i.e., the bullet point right above the monotonic stack definition) illustrates how it's possible to make "next" and "previous" value determinations as we process each element before adding it to the monotonic stack. Let's examine how we might be able to do this efficiently by combining the two templates from the two sections above:

General template for "next value" problems
def fn(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_B = nums[i]
        # the comparison operator (?) dictates what A's next value B represents
        # (<)  next larger value (weakly decreasing stack)
        # (<=) next larger or equal value (strictly decreasing stack)
        # (>)  next smaller value (weakly increasing stack)
        # (>=) next smaller or equal value (strictly increasing stack)
        while stack and nums[stack[-1]] ? val_B:
            idx_val_A = stack.pop()
            ans[idx_val_A] = val_B

        # why shouldn't we make a "previous value" determination here
        # before adding the current element to the stack?

        stack.append(i)
    
    # process elements that never had a "next" value that satisfied the criteria
    while stack:
        idx_val_A = stack.pop()
        ans[idx_val_A] = -1
    
    return ans

General template for "previous value" problems
def fn(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_A = nums[i]
        # the comparison operator (?) dictates what A's previous value B represents
        # (<=) previous larger (strictly decreasing)
        # (<)  previous larger or equal value (weakly decreasing)
        # (>=) previous smaller value (strictly increasing)
        # (>)  previous smaller or equal value (weakly increasing)
        while stack and nums[stack[-1]] ? val_A:
            stack.pop() # this template currently does not do anything with this value

            # why shouldn't we make "next value" determinations here
            # instead of doing nothing with the values popped from the stack?

            
        if stack:
            idx_val_B = stack[-1]
            val_B = nums[idx_val_B]
            ans[i] = val_B
        else:
            ans[i] = -1
        
        stack.append(i)
        
    return ans

Let's try to combine these templates by resolving the issues highlighted above. Our answer array will now be a list of lists structured in the following way: ans[i] == [prev, next], where prev and next indicate the "previous" and "next" values for each element at index i (i.e., the element nums[i]). Here's one way of doing this:

def fn(nums):
    n = len(nums)
    ans = [[None, None] for _ in range(n)]
    stack = []
    
    # the comparison operator (?) dictates what each element's PREVIOUS and NEXT values will be
    # (<=) PREVIOUS larger value and NEXT larger or equal value (strictly decreasing stack)
    # (<)  PREVIOUS larger or equal value and NEXT larger value (weakly decreasing stack)
    # (>=) PREVIOUS smaller value and NEXT smaller or equal value (strictly increasing stack)
    # (>)  PREVIOUS smaller or equal value and NEXT smaller value (weakly increasing stack)
    for i in range(n):
        while stack and nums[stack[-1]] ? nums[i]:
            idx = stack.pop() # NEXT values are now processed for each element popped from the stack
            ans[idx][1] = i
        
        # PREVIOUS value for current element is now processed (before adding it to the stack)
        if stack:
            ans[i][0] = stack[-1]
        else:
            ans[i][0] = -1
            
        stack.append(i)
    
    # process remaining values that had no "next" value
    while stack:
        idx = stack.pop()
        ans[idx][1] = -1
        
    return ans

Initialization of answer array

Answer arrays are often initialized as ans = [-1] * n, ans = [None] * n, etc., but it would be a mistake if we tried initializing ans in the combined template above as ans = [[None, None]] * n. Why? This expression essentially creates a list containing n references to the same list: [None, None]; hence, if one of these lists is modified, then all of them get modified (because they all refer to the same list in memory). That's definitely not the intention! This is because entities such as -1, None, etc., are values and not references whereas lists are references. The simple fix for this issue is to simply create n distinct lists in ans, where each list starts as [None, None].

If we allow ourselves the freedom to tidy things up a bit, then we can express the code above in a much more concise manner (by condensing logic as well as removing code comments):

def fn(nums):
    n = len(nums)
    ans = [[-1, -1] for _ in range(n)]
    stack = []
    for i in range(n):
        while stack and nums[stack[-1]] ? nums[i]:
            idx = stack.pop()
            ans[idx][1] = i
        ans[i][0] = -1 if not stack else stack[-1]
        stack.append(i)
    return ans

What changes were made above to condense things so much? See if you can determine that for yourself before looking at the final template below which contains several code comments:

Combined templates for finding previous and next values in a single pass
def fn(nums):
    n = len(nums)
    ans = [[-1, -1] for _ in range(n)] # default values for missing PREVIOUS and NEXT values, respectively
    stack = [] # monotonic stack
    
    # the comparison operator (?) dictates what each element's PREVIOUS and NEXT values will be
    # (<=) PREVIOUS larger value and NEXT larger or equal value (strictly decreasing stack)
    # (<)  PREVIOUS larger or equal value and NEXT larger value (weakly decreasing stack)
    # (>=) PREVIOUS smaller value and NEXT smaller or equal value (strictly increasing stack)
    # (>)  PREVIOUS smaller or equal value and NEXT smaller value (weakly increasing stack)
    for i in range(n):
        while stack and nums[stack[-1]] ? nums[i]:
            # NEXT values processed
            idx = stack.pop()
            ans[idx][1] = i # use nums[i] instead of i to directly record array values instead of indexes
        # PREVIOUS values processed
        ans[i][0] = -1 if not stack else stack[-1] # use nums[stack[-1]] instead of stack[-1] 
                                                   # to directly record array values instead of indexes 
        stack.append(i)
    
    return ans

The template above is remarkably powerful given what it accomplishes in a single pass. If we execute fn on the sample input array nums = [3, 4, 4, 5, 4, 1], then we get the following outputs for each comparison operator used to maintain the stack invariant:

(<=) PREVIOUS larger, NEXT larger or equal
#  0  1  2  3  4  5  (index values)
# [3, 4, 4, 5, 4, 1] (input array)
# output:
[
  [-1,  1], # previous larger value for nums[0] == 3 does not exist (-1)
            # next larger or equal value for nums[0] == 3 is nums[1] == 4

  [-1,  2], # previous larger value for nums[1] == 4 does not exist (-1)
            # next larger or equal value for nums[1] == 4 is nums[2] == 4
  
  [-1,  3], # previous larger value for nums[2] == 4 does not exist (-1)
            # next larger or equal value for nums[2] == 4 is nums[3] == 5

  [-1, -1], # previous larger value for nums[3] == 5 does not exist (-1)
            # next larger or equal value for nums[3] == 5 does not exist (-1)
  
  [ 3, -1], # previous larger value for nums[4] == 4 is nums[3] == 5
            # next larger or equal value for nums[4] == 4 does not exist (-1)
  
  [ 4, -1], # previous larger value for nums[5] == 1 is nums[4] == 5
            # next larger or equal value for nums[5] == 1 does not exist (-1)
]

(<) PREVIOUS larger or equal, NEXT larger
#  0  1  2  3  4  5  (index values)
# [3, 4, 4, 5, 4, 1] (input array)
# output:
[
  [-1,  1], # previous larger or equal value for nums[0] == 3 does not exist (-1)
            # next larger value for nums[0] == 3 is nums[1] == 4

  [-1,  3], # previous larger or equal value for nums[1] == 4 does not exist (-1)
            # next larger value for nums[1] == 4 is nums[3] == 5
  
  [ 1,  3], # previous larger or equal value for nums[2] == 4 does not exist (-1)
            # next larger value for nums[2] == 4 is nums[3] == 5

  [-1, -1], # previous larger or equal value for nums[3] == 5 does not exist (-1)
            # next larger value for nums[3] == 5 does not exist (-1)
  
  [ 3, -1], # previous larger or equal value for nums[4] == 4 is nums[3] == 5
            # next larger value for nums[4] == 4 does not exist (-1)
  
  [ 4, -1], # previous larger or equal value for nums[5] == 1 is nums[4] == 5
            # next larger value for nums[5] == 1 does not exist (-1)
]

(>=) PREVIOUS smaller, NEXT smaller or equal
#  0  1  2  3  4  5  (index values)
# [3, 4, 4, 5, 4, 1] (input array)
# output:
[
  [-1,  5], # previous smaller value for nums[0] == 3 does not exist (-1)
            # next smaller or equal value for nums[0] == 3 is nums[5] == 1

  [ 0,  2], # previous smaller value for nums[1] == 4 is nums[0] == 3
            # next smaller or equal value for nums[1] == 4 is nums[2] == 4
  
  [ 0,  4], # previous smaller value for nums[2] == 4 is nums[0] == 3
            # next smaller or equal value for nums[2] == 4 is nums[4] == 4

  [ 2,  4], # previous smaller value for nums[3] == 5 is nums[2] == 4
            # next smaller or equal value for nums[3] == 5 is nums[4] == 4
  
  [ 0,  5], # previous smaller value for nums[4] == 4 is nums[0] == 3
            # next smaller or equal value for nums[4] == 4 is nums[5] == 1
  
  [-1, -1], # previous smaller value for nums[5] == 1 does not exist (-1)
            # next smaller or equal value for nums[5] == 1 does not exist (-1)
]

(>) PREVIOUS smaller or equal, NEXT smaller
#  0  1  2  3  4  5  (index values)
# [3, 4, 4, 5, 4, 1] (input array)
# output:
[
  [-1,  5], # previous smaller or equal value for nums[0] == 3 does not exist (-1)
            # next smaller value for nums[0] == 3 is nums[5] == 1

  [ 0,  5], # previous smaller or equal value for nums[1] == 4 is nums[0] == 3
            # next smaller value for nums[1] == 4 is nums[5] == 1
  
  [ 1,  5], # previous smaller or equal value for nums[2] == 4 is nums[1] == 4
            # next smaller value for nums[2] == 4 is nums[5] == 1

  [ 2,  4], # previous smaller or equal value for nums[3] == 5 is nums[2] == 4
            # next smaller value for nums[3] == 5 is nums[4] == 4
  
  [ 2,  5], # previous smaller or equal value for nums[4] == 4 is nums[2] == 4
            # next smaller value for nums[4] == 4 is nums[5] == 1
  
  [-1, -1], # previous smaller or equal value for nums[5] == 1 does not exist (-1)
            # next smaller value for nums[5] == 1 does not exist (-1)
]

Templates for generalized monotonic stacks and deques

note

The content in this section is largely meant for standalone reference (i.e., it contains repeated information if you've read all of the previous content in this post). You can safely skip ahead to the LeetCode practice problems and/or the solved practice problems if you've read everything above in this post.

The templates below are constructed in a way such that the index values are being added to the stack or (double-ended) queue as opposed to the values themselves. This is because index values are often needed since they supply additional information and make it possible to distinguish between values that might otherwise be considered identical. For example, if nums = [1, 1], then nums[0] == nums[1] but 0 != 1; that is, the values of 1 are identicial but their indexed positions are not.

The foundation of all possible monotonic stack and queue templates is the same and hinges on two important pieces of information:

Will elements possibly need to be removed from the left of the index collection at some point? If so, use a deque (otherwise use a simple stack). An element(s) is generally removed from the left of the deque after the deque's increasing/decreasing invariant has been maintained and the current element has been added to the right of the deque — usually some condition is violated that stipulates deque elements should be removed from the left (e.g., an invalid index for a sliding window is a common example).

Maintaining the increasing/decreasing invariant for the collection (stack or deque) always uses stack-like operations: we remove from the right or top (i.e., "pop") every single value that would result in the invariant being violated once the current element is added to the right or top (i.e., "push"). In this sense, a monotonic "queue" is really a misnomer since the addition and removal of elements to maintain the invariant is always performed in LIFO fashion (last in first out); that is, the "push" and "pop" operations needed to maintain the deque invariant are fundamentally stack-like in nature. It's only if we need to remove elements from the left that the idea of a queue enters the picture, where a FIFO operation is needed (i.e., first in first out). Hence, we only ever really consider monotonic stacks or deques (double-ended queues).

How do the values referred to in your index collection need to progress from left to right? Should the values be strictly increasing or strictly decreasing? Should duplicate values be allowed (i.e., weakly increasing or weakly decreasing)? The value comparison you use in the condition of the while loop determines what kind of invariant you will maintain for your index collection.

The core part of maintaining the invariant for any index collection is the following:

# ...
for i in range(len(nums)):
    curr_num = nums[i]
    while index_collection and nums[index_collection[-1]] ? curr_num:
        index_collection.pop()
    index_collection.append(i)
# ...

Above, ? refers to the value comparison used to maintain the index collection's invariant. Solutions involving monotonic stacks generally involve finding each element's "next" or "previous" value in some comparative way (i.e., greater/smaler or equal to):

Template for finding A's next value B
def fn(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_B = nums[i]
        # the comparison operator (?) dictates what A's next value B represents
        # (<)  next larger value (weakly decreasing stack)
        # (<=) next larger or equal value (strictly decreasing stack)
        # (>)  next smaller value (weakly increasing stack)
        # (>=) next smaller or equal value (strictly increasing stack)
        while stack and nums[stack[-1]] ? val_B:
            idx_val_A = stack.pop()
            ans[idx_val_A] = val_B
        stack.append(i)
    
    # process elements that never had a "next" value that satisfied the criteria
    while stack:
        idx_val_A = stack.pop()
        ans[idx_val_A] = -1
    
    return ans

Template for finding A's previous value B
def fn(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_A = nums[i]
        # the comparison operator (?) dictates what A's previous value B represents
        # (<=) previous larger (strictly decreasing)
        # (<)  previous larger or equal value (weakly decreasing)
        # (>=) previous smaller value (strictly increasing)
        # (>)  previous smaller or equal value (weakly increasing)
        while stack and nums[stack[-1]] ? val_A:
            stack.pop()
            
        if stack:
            idx_val_B = stack[-1]
            val_B = nums[idx_val_B]
            ans[i] = val_B
        else:
            ans[i] = -1
        
        stack.append(i)
        
    return ans

Combined templates for previous and next values
def fn(nums):
    n = len(nums)
    ans = [[-1, -1] for _ in range(n)] # default values for missing PREVIOUS and NEXT values, respectively
    stack = [] # monotonic stack
    
    # the comparison operator (?) dictates what each element's PREVIOUS and NEXT values will be
    # (<=) PREVIOUS larger value and NEXT larger or equal value (strictly decreasing stack)
    # (<)  PREVIOUS larger or equal value and NEXT larger value (weakly decreasing stack)
    # (>=) PREVIOUS smaller value and NEXT smaller or equal value (strictly increasing stack)
    # (>)  PREVIOUS smaller or equal value and NEXT smaller value (weakly increasing stack)
    for i in range(n):
        while stack and nums[stack[-1]] ? nums[i]:
            # NEXT values processed
            idx = stack.pop()
            ans[idx][1] = i # use nums[i] instead of i to directly record array values instead of indexes
        # PREVIOUS values processed
        ans[i][0] = -1 if not stack else stack[-1] # use nums[stack[-1]] instead of stack[-1] 
                                                   # to directly record array values instead of indexes 
        stack.append(i)
    
    return ans

Solutions involving monotonic deques are usually almost identical to their monotonic stack equivalents but with the inclusion of some CONDITION being met that necessitates the removal of collection elements from the left. For example, suppose we're trying to find each element's next greater value, but we now have some CONDITION that, when met, means we need to remove the leftmost element of our collection:

Monotonic deque (weakly decreasing)
from collections import deque
def fn(nums):
    dec_queue = deque()
    ans = []
    
    for i in range(len(nums)):
        curr_num = nums[i]
        while dec_queue and nums[dec_queue[-1]] < curr_num:
            dec_queue.pop()
        dec_queue.append(i)
        
        if CONDITION:
            dec_queue.popleft()
        
    return ans

Monotonic stack (weakly decreasing)

def fn(nums):
    dec_stack = []
    ans = []
    
    for i in range(len(nums)):
        curr_num = nums[i]
        while dec_stack and nums[dec_stack[-1]] < curr_num:
            dec_stack.pop()
        dec_stack.append(i)
        



    return ans

Monotonic stack

"Next height" problems solved with code template

All of the problems below use heights = [14, 17, 13, 14, 14, 19, 12, 14, 18] as the input. Each problem requests a height value in relation to the current height value — if such a value is not found, then -1 should be reported.

Next height greater than current height

def next_greater_height(heights):
    dec_stack = [] # monotonically decreasing stack (duplicates allowed)
    ans = [-1] * len(heights)
    
    for i in range(len(heights)):
        curr_height = heights[i]
        while dec_stack and heights[dec_stack[-1]] < curr_height:
            prev_height_index = dec_stack.pop()
            ans[prev_height_index] = curr_height
        dec_stack.append(i)
        
    return ans

# Input
[14, 17, 13, 14, 14, 19, 12, 14, 18]

# Output
[17, 19, 14, 19, 19, -1, 14, 18, -1]

Next height greater than or equal to current height

def next_greater_than_or_equal_to_height(heights):
    dec_stack = [] # monotonically decreasing stack (duplicates not allowed)
    ans = [-1] * len(heights)
    
    for i in range(len(heights)):
        curr_height = heights[i]
        while dec_stack and heights[dec_stack[-1]] <= curr_height:
            prev_height_index = dec_stack.pop()
            ans[prev_height_index] = curr_height
        dec_stack.append(i)
        
    return ans

# Input
[14, 17, 13, 14, 14, 19, 12, 14, 18]

# Output
[17, 19, 14, 14, 19, -1, 14, 18, -1]

Next height smaller than current height

def next_smaller_height(heights):
    inc_stack = [] # monotonically increasing stack (duplicates allowed)
    ans = [-1] * len(heights)
    
    for i in range(len(heights)):
        curr_height = heights[i]
        while inc_stack and heights[inc_stack[-1]] > curr_height:
            prev_height_index = inc_stack.pop()
            ans[prev_height_index] = curr_height
        inc_stack.append(i)
        
    return ans        

# Input
[14, 17, 13, 14, 14, 19, 12, 14, 18]

# Output
[13, 13, 12, 12, 12, 12, -1, -1, -1]

Next height smaller than or equal to current height

def next_smaller_than_or_equal_to_height(heights):
    inc_stack = [] # monotonically increasing stack (duplicates not allowed)
    ans = [-1] * len(heights)
    
    for i in range(len(heights)):
        curr_height = heights[i]
        while inc_stack and heights[inc_stack[-1]] >= curr_height:
            prev_height_index = inc_stack.pop()
            ans[prev_height_index] = curr_height
        inc_stack.append(i)
        
    return ans  

# Input
[14, 17, 13, 14, 14, 19, 12, 14, 18]

# Output
[13, 13, 12, 14, 12, 12, -1, -1, -1]

Monotonic stack (template for finding A's next value B)
def fn(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_B = nums[i]
        # the comparison operator (?) dictates what A's next value B represents
        # (<)  next larger value (weakly decreasing stack)
        # (<=) next larger or equal value (strictly decreasing stack)
        # (>)  next smaller value (weakly increasing stack)
        # (>=) next smaller or equal value (strictly increasing stack)
        while stack and nums[stack[-1]] ? val_B:
            idx_val_A = stack.pop()
            ans[idx_val_A] = val_B
        stack.append(i)
    
    # process elements that never had a "next" value that satisfied the criteria
    while stack:
        idx_val_A = stack.pop()
        ans[idx_val_A] = -1
    
    return ans

Monotonic stack (template for finding A's previous value B)
def fn(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_A = nums[i]
        # the comparison operator (?) dictates what A's previous value B represents
        # (<=) previous larger (strictly decreasing)
        # (<)  previous larger or equal value (weakly decreasing)
        # (>=) previous smaller value (strictly increasing)
        # (>)  previous smaller or equal value (weakly increasing)
        while stack and nums[stack[-1]] ? val_A:
            stack.pop()
            
        if stack:
            idx_val_B = stack[-1]
            val_B = nums[idx_val_B]
            ans[i] = val_B
        else:
            ans[i] = -1
        
        stack.append(i)
        
    return ans

Monotonic stack (combined templates for previous and next values)
def fn(nums):
    n = len(nums)
    ans = [[-1, -1] for _ in range(n)] # default values for missing PREVIOUS and NEXT values, respectively
    stack = [] # monotonic stack
    
    # the comparison operator (?) dictates what each element's PREVIOUS and NEXT values will be
    # (<=) PREVIOUS larger value and NEXT larger or equal value (strictly decreasing stack)
    # (<)  PREVIOUS larger or equal value and NEXT larger value (weakly decreasing stack)
    # (>=) PREVIOUS smaller value and NEXT smaller or equal value (strictly increasing stack)
    # (>)  PREVIOUS smaller or equal value and NEXT smaller value (weakly increasing stack)
    for i in range(n):
        while stack and nums[stack[-1]] ? nums[i]:
            # NEXT values processed
            idx = stack.pop()
            ans[idx][1] = i # use nums[i] instead of i to directly record array values instead of indexes
        # PREVIOUS values processed
        ans[i][0] = -1 if not stack else stack[-1] # use nums[stack[-1]] instead of stack[-1] 
                                                   # to directly record array values instead of indexes 
        stack.append(i)
    
    return ans

Monotonic queue (deque)

Sliding window minimum problem solved with code template

Recall the problem statement:

You are given an array of integers nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Return an answer array that contains the minimum value for each sliding window of size k. For example, if the input array is nums = [11, 13, -11, -13, 15, 13, 16, 17] and k = 3, then the desired output or answer array would be [-11, -13, -13, -13, 13, 13].

The following illustration shows why the example above has the input and output it does:

Now for the solution based on the template code:

from collections import deque

def sliding_window_min(nums, k):
    queue = deque() # monotonic deque (weakly increasing)
    ans = []
    
    for i in range(len(nums)):
        curr_num = nums[i]
        while queue and nums[queue[-1]] > curr_num:
            queue.pop()
        queue.append(i)

        # remove the leftmost deque element if it is the leftmost index of the previous window
        # (i.e., it is not a valid index for the _current_ window)
        if queue[0] == i - k:
            queue.popleft()
        
        # only start adding to the answer array 
        # once the window has grown to the required size
        if i >= k - 1:
            ans.append(nums[queue[0]])
            
    return ans

from collections import deque

def fn(nums):
    queue = deque() # monotonic deque
    ans = []
    
    for i in range(n):
        val_B = nums[i]
        # the comparison operator (?) dictates what A's next value B represents
        # (<)  next larger value (weakly decreasing queue)
        # (<=) next larger or equal value (strictly decreasing queue)
        # (>)  next smaller value (weakly increasing queue)
        # (>=) next smaller or equal value (strictly increasing queue)
        while queue and nums[queue[-1]] ? val_B:
            idx_val_A = queue.pop()
            ans[idx_val_A] = val_B
        queue.append(i)

        if CONDITION:
            queue.popleft()
    
    # process elements that never had a "next" value that satisfied the criteria
    while queue:
        idx_val_A = queue.pop()
        ans[idx_val_A] = -1
    
    return ans

LeetCode practice problems

There are many ways to practice solving problems where monotonic stacks or (double-ended) queues play a pivotal role in crafting an optimal solution. LeetCode itself is a treasure trove for these kinds of problems.

Monotonic stacks

There are currently 58 problems on LeetCode tagged as being monotonic stack problems:

Monotonic queues

There are currently 15 problems on LeetCode tagged as being monotonic queue problems:

Solved practice problems

The problems below all appear on the LeetCode platform. The notation used in many of the provided solutions matches the notation used in the templates for "next" and "previous" values for the sake of clarity (this arguably makes it easier to see exactly how each template is being applied and/or modified).

Each solved practice problem consists of three elements:

The problem statement (followed by a horizontal dividing line). If you want to see examples of desired outputs for different inputs, then right-click the problem title in each widget to visit the link to view the problem in its entirety on the LeetCode platform.
An accepted solution (i.e., a solution which is accepted for the given problem on the LeetCode platform).
Commentary on the provided solution that is accepted (minimal in some cases and quite extensive in others).

The final two solved practice problems, LC 907. Sum of Subarray Minimums and LC 2104. Sum of Subarray Ranges, are addressed more thoroughly in this post's "epilogue".

LC 739. Daily Temperatures

Given an array of integers temperatures that represents the daily temperatures, return an array answer such that answer[i] is the number of days you have to wait after the ith day to get a warmer temperature. If there is no future day for which this is possible, keep answer[i] == 0 instead.

class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        n = len(temperatures)
        ans = [None] * n
        stack = []
        
        for i in range(n):
            val_A = temperatures[i]
            # try to find the next larger temperature, val_B,
            # for the current temperature, val_A
            while stack and temperatures[stack[-1]] < val_A:
                idx_val_B = stack.pop()
                ans[idx_val_B] = i - idx_val_B
            stack.append(i)
        
        # remaining temperatures, val_A, have no next larger temperature, val_B
        while stack:
            idx_val_A = stack.pop()
            ans[idx_val_A] = 0
            
        return ans

The approach above is almost a direct application of the template for next value problems, where we're trying to find the next larger value for each value we encounter. We use the difference in indexes to determine how many days there are to wait.

LC 239. Sliding Window Maximum

Return the max sliding window.

class Solution:
    def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
        n = len(nums)
        dec_queue = deque() # monotonic deque (weakly decreasing)
        ans = []
        for i in range(n):
            curr_num = nums[i]
            # maintain the weakly decreasing deque
            while dec_queue and nums[dec_queue[-1]] < curr_num:
                dec_queue.pop()
            
            # check to see if leftmost value of the deque
            # is now actually an invalid index
            if dec_queue and dec_queue[0] == i - k:
                dec_queue.popleft()
            
            dec_queue.append(i)
            
            # only add window maximums to the answer array
            # once the required length has been reached
            if i >= k - 1:
                ans.append(nums[dec_queue[0]])
                
        return ans

We're not trying to find a "next" or "previous" anything. We're trying to maintain a sliding window maximum. A monotonic deque that is weakly decreasing is the tool of choice here (weakly decreasing instead of strictly since the same window can have duplicated maxima) since access to the leftmost element will always be the maximum. Additionally, if sliding the window results in invalidating the leftmost index of the deque pointing to the maximum, then we can simply pop from the left.

LC 1438. Longest Continuous Subarray With Absolute Diff Less Than or Equal to Limit

Given an array of integers nums and an integer limit, return the size of the longest non-empty subarray such that the absolute difference between any two elements of this subarray is less than or equal to limit.

class Solution:
    def longestSubarray(self, nums: List[int], limit: int) -> int:
        n = len(nums)
        dec_queue = deque() # monotonic deque (weakly decreasing) for the maximums
        inc_queue = deque() # monotonic deque (weakly increasing) for the minimums
        left = ans = 0
        
        for right in range(n):
            curr_num = nums[right]
            
            # maintain the deque invariants
            while dec_queue and nums[dec_queue[-1]] < curr_num:
                dec_queue.pop()
            while inc_queue and nums[inc_queue[-1]] > curr_num:
                inc_queue.pop()
                
            dec_queue.append(right)
            inc_queue.append(right)
                
            # update sliding window to ensure the window is valid
            while left <= right and nums[dec_queue[0]] - nums[inc_queue[0]] > limit:
                # remove possibly invalidated indexes from the deques once the window has shifted
                if dec_queue[0] == left:
                    dec_queue.popleft()
                if inc_queue[0] == left:
                    inc_queue.popleft()
                left += 1

            # update the answer with the length of the current valid window
            ans = max(ans, right - left + 1)
        
        return ans

We're not trying to find a "next" or "previous" anything. We need to somehow process all subarrays to find the longest one such that the absolute difference between any two elements in the subarray is less than or equal to limit. The absolute difference is biggest (and thus threatens to exceed limit) when we take the difference between the subarray's maximum and its minimum. Hence, we're essentially trying to maintain a subarray's maximum and minimum. The previous practice problem, LC 239. Sliding Window Maximum, showed how to artfully handle maintaining a sliding window maximum. We employ similar logic here to maintain a sliding window maximum and minimum. Two deques are needed in order to do this effectively.

LC 496. Next Greater Element I

You are given two integer arrays nums1 and nums2 both of unique elements, where nums1 is a subset of nums2.

Find all the next greater numbers for nums1's elements in the corresponding places of nums2.

The Next Greater Number of a number x in nums1 is the first greater number to its right in nums2. If it does not exist, return -1 for this number.

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        queries = {}
        stack = []
        
        # determine "next greater" values in nums2
        for i in range(len(nums2)):
            val_B = nums2[i]
            while stack and nums2[stack[-1]] < val_B:
                idx_val_A = stack.pop()
                val_A = nums2[idx_val_A]
                queries[val_A] = val_B
            stack.append(i)
        
        # remaining values have no next greater value (default to -1)
        while stack:
            idx_val_A = stack.pop()
            val_A = nums2[idx_val_A]
            queries[val_A] = -1
            
        # the queries hash map tells us the next greater value
        # for each value queried from nums1
        ans = [None] * len(nums1)
        for i in range(len(nums1)):
            ans[i] = queries[nums1[i]]
            
        return ans

The framing for this problem is somewhat odd at first. Nonetheless, once we can wrap our heads around what exactly is being asked, our approach is almost a direct application of the template for next value problems (specifically next greater value, of course). The code above can be cleaned up a little by using defaultdict from the collections module and not adhering so closely to the syntax of the template:

class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        queries = defaultdict(lambda: -1)
        stack = []
        
        for i in range(len(nums2)):
            val_B = nums2[i]
            while stack and nums2[stack[-1]] < val_B:
                idx_val_A = stack.pop()
                val_A = nums2[idx_val_A]
                queries[val_A] = val_B
            stack.append(i)
        
        ans = [None] * len(nums1)
        for i in range(len(nums1)):
            ans[i] = queries[nums1[i]]
            
        return ans

LC 503. Next Greater Element II

Given a circular integer array nums (i.e., the next element of nums[nums.length - 1] is nums[0]), return the next greater number for every element in nums.

The next greater number of a number x is the first greater number to its traversing-order next in the array, which means you could search circularly to find its next greater number. If it doesn't exist, return -1 for this number.

class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        n = len(nums)
        ans = [None] * n
        stack = []
        
        for i in range(n * 2):
            val_B = nums[i % n]
            while stack and nums[stack[-1]] < val_B:
                idx_val_A = stack.pop()
                ans[idx_val_A] = val_B

            # only add elements to the stack on the first full pass
            if i < n:
                stack.append(i)
            else:
                # otherwise the remaining values (if there are any)
                # never had a next greater element; hence, we simply
                # make another full pass to see if any element is greater
                # than the current element in the stack and then pop the
                # element from the stack if the answer is affirmative
                if stack and nums[stack[-1]] < nums[i % n]:
                    idx_val_A = stack.pop()
                    ans[idx_val_A] = nums[i % n]
        
        # the remaining values in the stack are those that do not have a next
        # greater element despite two full passes; we report -1 for these values
        while stack:
            idx_val_A = stack.pop()
            ans[idx_val_A] = -1
            
        return ans

This problem is the same as LC 496. Next Greater Element I, but there's a significant twist where now we're considering the array to be circular. This may sound wild at first, but the change in approach is actually quite simple: we can cycle back through the original array by iterating a total of 2 * n times where n = len(nums). To ensure we don't get an "index out of bounds" error, we use a standard trick, namely the modulus operator %: i % n. Hence, if n = 10, and i = 10, then we're really looking at the element at index i = 0 since 10 % 10 == 0.

The approach above is a slightly tweaked application of the template for next value problems.

LC 901. Online Stock Span

Write a class StockSpanner which collects daily price quotes for some stock, and returns the span of that stock's price for the current day.

The span of the stock's price today is defined as the maximum number of consecutive days (starting from today and going backwards) for which the price of the stock was less than or equal to today's price.

For example, if the price of a stock over the next 7 days were [100, 80, 60, 70, 60, 75, 85], then the stock spans would be [1, 1, 1, 2, 1, 4, 6].

Approach 1 (conventional approach for finding previous larger value; recommended)

class StockSpanner:
    def __init__(self):
        self.stack = []
        self.idx = 0

    def next(self, price: int) -> int:
        val_A = price
        while self.stack and self.stack[-1][0] <= price:
            self.stack.pop()
            
        if self.stack:
            idx_val_B = self.stack[-1][1]
            val_B = self.stack[-1][0]
            stock_span = self.idx - idx_val_B
        else:
            stock_span = self.idx + 1
            
        self.stack.append([val_A, self.idx])
        self.idx += 1
        
        return stock_span

The approach above is almost a direct application of the template for previous value problems, where we're finding the previous larger value. It's not necessary to use the val_A/val_B nomenclature in the solution above — it's simply done to show how similar an acceptable solution is to the bare bones previous value template.

Why are we interested in finding the previous larger value for each new value we encounter? Because the stock span of the new/current value is effectively defined as the total number of previous less than or equal to values. Finding the previous larger value tells us where the current value's stock span begins.

Approach 2 (more sophisticated approach by cleverly accumulating stock spans; instructional)

class StockSpanner:
    def __init__(self):
        self.dec_stack = [] # monotonic stack (strictly decreasing)

    def next(self, price: int) -> int:
        curr_span = 1
        while self.dec_stack and self.dec_stack[-1][0] <= price:
            prev_span = self.dec_stack.pop()[1]
            curr_span += prev_span
        self.dec_stack.append([price, curr_span])
        return curr_span

Additional complexity with minimal gains

The solution approach below is characteristic of more advanced monotonic stack problems, where we cleverly manipulate elements on the stack itself, where the elements aren't just array values or even indexes of array values but collections of values, specifically 2-element arrays where the first element is the price itself and the second element is the price's stock span. In the previous approach, we used 2-element arrays as well, but we used what people normally use with monotonic stacks, namely the array values and the indexes of the array values. Encoding stock span values within the monotonic stack itself makes this a more sophisticated approach. There may be fewer lines of code in this more sophisticated approach, but it may not be worth the hassle to understand at first since there aren't any notable gains in performance.

It turns out we can solve this problem in a slightly more nuanced way than what was outlined in the previous approach, specifically by how we modify and use elements on the stack.

What information do we truly need at each step in order for next to report the appropriate value for each newly added price quote? We need the cumulative span between

the current price (included) and
the most recent price greater than the current price (not included)

Is it possible to maintain our stack in a way that supports this? Yes, if we allow ourselves to encode additional information in the stack:

The stack should store pairs of stock prices and their corresponding stock spans (as opposed to stock prices and their corresponding index values in the previous approach).
Each stack entry is a pair consisting of the stock price and the maximum number of consecutive days the price was the highest (i.e., the price's stock span).
When a new price is processed, all previous pairs for which the stock prices were less than or equal to the current price should be removed from the stack and their corresponding stock spans added to the current price's stock span. The current price and its new stock span should now be added to the stack.

Removing the pairs in the way referenced above ensures invalid stock prices are not used in future stock span calculations; for example, if the current price is 1000, then previous prices less than 1000 are no longer relevant and should be removed. If, however, a previous pair in our stack had a price equal to 1000, then would removing such a pair cause an issue? No, because the current price and its new stock span will be added to the stack.

Everything outlined above is easier to understand by means of a more robust example. Suppose the prices we'll encounter in sequence are the following: [70, 100, 90, 83, 84, 73, 74, 75, 76, 61, 62, 90, 42]. The block below shows how these prices would be processed using the ideas discussed above. The right side shows the next return value associated with each price (that price's stock span), where the span calculation always begins with 1 since the current price always contributes at least 1 to its stock span:

# Stock prices processed so far                       # MONOTONIC STACK (strictly decreasing) ... price's stock span
[70]                                                  # [[70, 1]] ... 1
[70, 100]                                             # [[100, 2]] ... 1 + 1 
[70, 100, 90]                                         # [[100, 2], [90, 1]] ... 1
[70, 100, 90, 83]                                     # [[100, 2], [90, 1], [83, 1]] ... 1
[70, 100, 90, 83, 84]                                 # [[100, 2], [90, 1], [84, 2]] ... 1 + 1
[70, 100, 90, 83, 84, 73]                             # [[100, 2], [90, 1], [84, 2], [73, 1]] ... 1
[70, 100, 90, 83, 84, 73, 74]                         # [[100, 2], [90, 1], [84, 2], [74, 2]] ... 1 + 1
[70, 100, 90, 83, 84, 73, 74, 75]                     # [[100, 2], [90, 1], [84, 2], [75, 3]] ... 1 + 2
[70, 100, 90, 83, 84, 73, 74, 75, 76]                 # [[100, 2], [90, 1], [84, 2], [76, 4]] ... 1 + 3
[70, 100, 90, 83, 84, 73, 74, 75, 76, 61]             # [[100, 2], [90, 1], [84, 2], [76, 4], [61, 1]] ... 1
[70, 100, 90, 83, 84, 73, 74, 75, 76, 61, 62]         # [[100, 2], [90, 1], [84, 2], [76, 4], [62, 2]] ... 1 + 1
[70, 100, 90, 83, 84, 73, 74, 75, 76, 61, 62, 90]     # [[100, 2], [90, 10]] ... 1 + 2 + 4 + 2 + 1
[70, 100, 90, 83, 84, 73, 74, 75, 76, 61, 62, 90, 42] # [[100, 2], [90, 10], [42, 1]] ... 1

The example above illustrates the mechanics behind how the stack is maintained in service of reporting each new price's stock span (i.e., the next function's return value). Observe how the reported stock span grows whenever an element gets popped from the stack. More important though is that no information is lost about previous stock prices when an element is popped from the stack since this information is effectively captured in each new element added to the stack. Specifically, each newly added element to the stack is a 2D-array whose first value is a stock price and its second value is the stock span of that stock price in relation to all previous stock prices.

In the longer example presented above, what would the return value be for the next function if we tried adding each of the following values separately (i.e., standalone addition, not in sequence):

41: The stack starts as [[100, 2], [90, 10], [42, 1]].
- The current stock span starts as 1.
- Since 42 is greater than 41, we should not remove anything from the stack. We just add the pair for the current price and its stock span [41, 1], to the stack: [[100, 2], [90, 10], [42, 1], [41, 1]].
- Return 1.
42: The stack starts as [[100, 2], [90, 10], [42, 1]].
- The current stock span starts as 1.
- Since 42 is less than or equal to 42, we pop the last element from the stack and add its stock span to the current price's stock span: 1 + 1 = 2.
- Add the pair of current price and its stock span, [42, 2], to the stack: [[100, 2], [90, 10], [42, 2]].
- Return 2.
150: The stack starts as [[100, 2], [90, 10], [42, 1]].
- The current stock span starts as 1.
- Since 42 is less than or equal to 150, we pop [42, 1] from the stack and add its stock span to the current stock span: 1 + 1 = 2.
- Since 90 is less than or equal to 150, we pop [90, 10] from the stack and add its stock span to the current stock span: 2 + 10 = 12.
- Since 100 is less than or equal to 150, we pop [100, 2] from the stack and add its stock span to the current stock span: 12 + 2 = 14.
- Add the pair of current price and its stock span, [150, 14], to the stack: [[150, 14]].
- Return 14.

LC 1475. Final Prices With a Special Discount in a Shop

Given the array prices where prices[i] is the price of the ith item in a shop. There is a special discount for items in the shop, if you buy the ith item, then you will receive a discount equivalent to prices[j] where j is the minimum index such that j > i and prices[j] <= prices[i], otherwise, you will not receive any discount at all.

Return an array where the ith element is the final price you will pay for the ith item of the shop considering the special discount.

class Solution:
    def finalPrices(self, prices: List[int]) -> List[int]:
        n = len(prices)
        stack = []
        
        for i in range(n):
            val_B = prices[i]
            while stack and prices[stack[-1]] >= val_B:
                idx_val_A = stack.pop()
                prices[idx_val_A] -= val_B # val_B is discount since it is next less or equal value to val_A
            stack.append(i)
        
        return prices

The approach above is almost a direct application of the template for next value problems, specifically the "next less or equal value" problem. For each price, we want to determine if we can obtain a discount, and a discount is only possible if a subsequent value is less than or equal to the current value, hence the approach outlined above.

LC 1063. Number of Valid Subarrays

Given an array A of integers, return the number of non-empty continuous subarrays that satisfy the following condition:

The leftmost element of the subarray is not larger than other elements in the subarray.

class Solution:
    def validSubarrays(self, nums: List[int]) -> int:
        n = len(nums)
        queries = [n] * n
        stack = []
        ans = 0
        
        for i in range(n):
            val_B = nums[i]
            while stack and nums[stack[-1]] > val_B:
                idx_val_A = stack.pop()
                queries[idx_val_A] = i
            stack.append(i)
        
        # query the next smaller value for each index of nums
        # the current index will be the included left endpoint 
        # and the queried value will be the excluded right endpoint
        # total number of subarrays contributed where the left endpoint
        # is the minimum: right - left (since right is excluded)
        for left in range(n):
            right = queries[left]
            ans += right - left # NOT "right - left + 1" because right is not included here
        
        return ans

The template for next value problems is valuable here since we're effectively looking for each value's "next smaller" value. Why? Because until we've found the current value's next smaller value, the current value is the minimum value (there may be other equal minimum values that contribute to the subarray count).

The deeper intuition for solving this problem strongly depends on understanding that if the window [left, right] and all its "sub-windows" satisfy some constraint for a subarray (i.e., leftmost element being minimal in this problem), then the number of valid subarrays is given by right - left + 1.

Brief explanation for number of valid subarrays being right - left + 1

If the subarray [left, right] and all its subarrays are valid, then how many such valid subarrays are there? This number is given by right - left + 1. Why? Because this number gives us the number of subarrays that end at index right:

[left, right]
[left + 1, right]
[left, + 2, right]
...
[right - 1, right]
[right, right] (single element, right)

The idea is that we can fix the right bound and then choose any value between left and right, inclusive, for the left bound such that the newly bounded subarray is valid. The total number of values to choose from is the length of the [left, right] subarray: right - left + 1.

LC 1673. Find the Most Competitive Subsequence

Given an integer array nums and a positive integer k, return the most competitive subsequence of nums of size k.

An array's subsequence is a resulting sequence obtained by erasing some (possibly zero) elements from the array.

We define that a subsequence a is more competitive than a subsequence b (of the same length) if in the first position where a and b differ, subsequence a has a number less than the corresponding number in b. For example, [1,3,4] is more competitive than [1,3,5] because the first position they differ is at the final number, and 4 is less than 5.

class Solution:
    def mostCompetitive(self, nums: List[int], k: int) -> List[int]:
        n = len(nums)
        stack = []
        
        for i in range(n):
            curr_num = nums[i]
            while stack and stack[-1] > curr_num and (n - i + len(stack) > k):
                stack.pop()
            
            if len(stack) < k:
                stack.append(nums[i])
        
        return stack

This is a really neat monotonic stack problem because the monotonic stack itself serves as part (or all) of the solution. The intuition is that the most competitive subsequence will be the one whose leftmost elements are as small as possible. A weakly increasing monotonic stack is almost all we need, but the main wrinkle for this problem is that the subsequence we return must be of length k. Hence, the goal effectively becomes the following: use a weakly increasing monotonic stack "as long as possible" (to ensure its leftmost elements are as small as possible) until we're forced to indiscriminately add elements in order to reach the required size of k.

Providing code comments may help in order to see the logic outlined above more clearly:

class Solution:
    def mostCompetitive(self, nums: List[int], k: int) -> List[int]:
        n = len(nums)
        stack = [] # monotonic stack (weakly increasing)
        
        for i in range(n):
            curr_num = nums[i]
            # number of elements remaining in nums (including curr_num): n - i
            # current number of elements in stack: len(stack)
            # goal: stack must ultimately have a total of k elements; hence,
            #   only consider popping an element from the stack if there are enough remaining
            #   elements in nums to ensure the final size of the stack is k
            while stack and stack[-1] > curr_num and (n - i + len(stack) > k):
                stack.pop()
            
            # the stack should never exceed k elements
            if len(stack) < k:
                stack.append(nums[i])
        
        return stack

LC 1944. Number of Visible People in a Queue

There are n people standing in a queue, and they numbered from 0 to n - 1 in left to right order. You are given an array heights of distinct integers where heights[i] represents the height of the ith person.

A person can see another person to their right in the queue if everybody in between is shorter than both of them. More formally, the ith person can see the jth person if i < j and min(heights[i], heights[j]) > max(heights[i+1], heights[i+2], ..., heights[j-1]).

Return an array answer of length n where answer[i] is the number of people the ith person can see to their right in the queue.

class Solution:
    def canSeePersonsCount(self, heights: List[int]) -> List[int]:
        n = len(heights)
        ans = [0] * n
        stack = [] # monotonic stack (decreasing)
        
        for i in range(n):
            curr_height = heights[i]
            while stack and heights[stack[-1]] < curr_height:
                idx_prev_smaller_height = stack.pop()
                ans[idx_prev_smaller_height] += 1
            
            if stack:
                ans[stack[-1]] += 1
                
            stack.append(i)
            
        return ans

The intuition for solving this problem is a bit harder to grok at first than some other monotonic stack problems. The picture LeetCode uses to illustrate its first example input of heights = [10,6,8,5,11,9] is actually quite helpful (which goes to show just how effective drawing things out can be sometimes!):

The desired output for this input is [3,1,2,1,1,0], and LeetCode gives the following explanation as to why:

Person 0 can see person 1, 2, and 4.
Person 1 can see person 2.
Person 2 can see person 3 and 4.
Person 3 can see person 4.
Person 4 can see person 5.
Person 5 can see no one since nobody is to the right of them.

Arguably the hardest part of this problem is figuring out how to deal with shorter people who are hidden behind taller people. This can lead to mistakes if we're not careful. For example, the number of visible people to the right of the person of height 10 (at index i = 0) must end at height 11 (at index i = 4) since 10 < 11, but the number of visible people is not 4 - 0 = 4 (the current person of height 10 would not be included in the count). The answer is actually 3 because the shorter person tucked behind the person of height 8 is not actually visible from the perspective of the person with height 10.

If we did try to use a monotonic stack to solve this problem, should our stack be increasing or decreasing? An increasing stack would mean we always have access to the person of minimum height and that doesn't seem to be to our advantage. What about a decreasing stack? We'd have access to the person of maximum height encountered so far, and that could possibly help. But how?

A possible hint is to generally consider when it makes sense to no longer keep track of someone of a certain height (i.e., essentially when this height should be popped from the stack). When height val_A encounters its next greater height, val_B, it no longer makes sense to keep track of val_A because the person with this height definitely cannot see anymore people to the right. It sounds more and more likely that our tool of choice here should be a decreasing monotonic stack (because each newly encountered height is the "next" height for heights on the stack, which we should start popping if any of them are smaller than this newly encountered height). But how do we account for the issue highlighted above where shorter people can be hidden behind taller people?

The answer reveals itself by working through the mechanics of maintaining a decreasing monotonic stack for the first example input: heights = [10,6,8,5,11,9]. We can initialize the corresponding answer array to be 0-filled and of the same length: [0,0,0,0,0,0]. Let's look at what happens when we try to process each height from left to right:

Height 10. This is the first height so the stack is currently empty. Push 10 to the stack (really its index) and move to the next element.
Height 6. Stack state: [10]. Is 10 < 6? No. We push 6 to the stack. Since 10 directly precedes the height of 6 in the stack, we add 1 to the answer slot for the person of height 10: ans = [1,0,0,0,0,0].
Height 8. Stack state: [10, 6]. Is 6 < 8? Yes. First add 1 to the answer slot for the person of height 6 (since the person of height 8 is visible to the right of person of height 6): ans = [1,1,0,0,0,0]. Pop 6 from the stack. The stack is non-empty which means the person of height 10 can see the person of height 8; hence, add 1 to the answer slot for the person of height 10: ans = [2,1,0,0,0,0]. Now push 8 to the stack.
Height 5. Stack state: [10, 8]. Is 8 < 5? No. We push 5 to the stack and also add 1 to the answer slot for height 8: ans = [2,1,1,0,0,0].
Height 11. Stack state: [10, 8, 5].
- Is 5 < 11? Yes. Add 1 to height 5's answer slot: ans = [2,1,1,1,0,0]. Pop 5 from the stack.
- Is 8 < 11? Yes. Add 1 to height 8's answer slot: ans = [2,1,2,1,0,0]. Pop 8 from the stack.
- Is 10 < 11? Yes. Add 1 to height 10's answer slot: ans = [3,1,2,1,0,0]. Pop 10 from the stack.
- The stack is now empty so no more comparisons can be made. Push 11 to the stack.
Height 9. Stack state: [11]. Is 11 < 9? No. We push 9 to the stack and add 1 to the answer slot for the person of height 11: ans = [3,1,2,1,1,0].

There are no more heights to process so we return the answer array [3,1,2,1,1,0], as desired.

The mechanics of working through the example above suggest the provided solution. The strategy is basically to maintain a monotonic decreasing stack:

If element height_A is popped from the stack because height_A < height_B, then this means height_A can see height_B to its right. So add 1 to the answer slot for height_A. We make these comparisons and pop elements from the stack (while updating the answer array) until either the stack is empty or we've reached an element greater than height_B.
If the stack is empty, then simply push height_B to the stack and move on. If, however, the stack is non-empty after all the removals above, then the element at the top of the stack can see height_B so its answer slot should have 1 added to it. Then push height_B to the stack.

The process above continues until we've exhausted all heights.

LC 2398. Maximum Number of Robots Within Budget

You have n robots. You are given two 0-indexed integer arrays, chargeTimes and runningCosts, both of length n. The ith robot costs chargeTimes[i] units to charge and costs runningCosts[i] units to run. You are also given an integer budget.

The total cost of running k chosen robots is equal to max(chargeTimes) + k * sum(runningCosts), where max(chargeTimes) is the largest charge cost among the k robots and sum(runningCosts) is the sum of running costs among the k robots.

Return the maximum number of consecutive robots you can run such that the total cost does not exceed budget.

class Solution:
    def maximumRobots(self, chargeTimes: List[int], runningCosts: List[int], budget: int) -> int:
        dec_queue = deque() # monotonic deque (weakly decreasing) for charge times
        left = window_sum = ans = 0
        
        for right in range(len(chargeTimes)):
            # maintain monotonic deque to ensure maximum charge time in window is quickly accessible
            curr_charge = chargeTimes[right]
            while dec_queue and chargeTimes[dec_queue[-1]] < curr_charge:
                dec_queue.pop()
            dec_queue.append(right)
            
            # maintain total running cost of sliding window
            curr_running_cost = runningCosts[right]
            window_sum += curr_running_cost
            
            while left <= right and dec_queue and chargeTimes[dec_queue[0]] + (right - left + 1) * window_sum > budget:
                # adjust window_sum to reflect new sliding window's total running cost
                window_sum -= runningCosts[left]
                # remove leftmost queue element if index is no longer valid after shifting window
                if dec_queue[0] == left:
                    dec_queue.popleft()
                left += 1
            
            ans = max(ans, right - left + 1)
            
        return ans

Arguably one of the hardest parts of this problem is fully understanding the problem statement itself. Specifically, the total cost formula max(chargeTimes) + k * sum(runningCosts) is somewhat confusing since realistically there's no need to multiply the sum of running costs by k; nonetheless, the problem statement dictates that the total cost formula stands as detailed above — we must use it in our solution.

Since the robots being used as part of the solution ultimately must be consecutive, this is a hint that a sliding window may be relevant. Since we always need the maximum of the charge values for the robots being used, it seems like we will need to maintain a sliding window maximum, which is where a monotonic deque can shine. A weakly decreasing monotonic deque should be used since a sliding window's maximum may not be unique. The rest of the problem then simply becomes maintaining the monotonic deque effectively while sliding the window (and maintaining the window sum as well for the total running cost).

LC 907. Sum of Subarray Minimums

Given an array of integers arr, find the sum of min(b), where b ranges over every (contiguous) subarray of arr. Since the answer may be large, return the answer modulo 10⁹ + 7.

This is a tough problem and is comprehensively dissected in the epilogue. The optimized solution in Approach 1 directly stems from the discussion in the epilogue. Approach 2, which is arguably a good bit easier to come up with, stems from the discussion in the last bullet point of the important observations section (i.e., the bullet point right above the monotonic stack definition).

Approach 1

class Solution:
    def sumSubarrayMins(self, arr: List[int]) -> int:
        n = len(arr)
        stack = []
        ans = 0
        MOD = 10 ** 9 + 7
        
        for i in range(n + 1):
            while stack and (i == n or arr[stack[-1]] >= arr[i]):
                curr_min_idx = stack.pop()
                curr_min = arr[curr_min_idx]
                left_boundary = -1 if not stack else stack[-1]
                right_boundary = i
                num_subarrays = (curr_min_idx - left_boundary) * (right_boundary - curr_min_idx)
                contribution = curr_min * num_subarrays
                ans += contribution
            stack.append(i)
            
        return ans % MOD

Approach 2

class Solution:
    def sumSubarrayMins(self, arr: List[int]) -> int:
        def minimum_boundaries(nums):
            n = len(nums)
            # missing previous values assigned as -1 (just before leftmost boundary)
            # missing next values assigned as n (just after rightmost boundary)
            ans = [[-1, n] for _ in range(n)]
            stack = [] # monotonic stack
            
            # the comparison operator (?) dictates what each element's PREVIOUS and NEXT values will be
            # (>=) PREVIOUS smaller value and NEXT smaller or equal value (strictly increasing stack)
            #       (good for finding minimums, non-strict to left and strict to right)
            # (>)  PREVIOUS smaller or equal value and NEXT smaller value (weakly increasing stack)
            #       (good for finding minimums, strict to left and non-strict to right)
            for i in range(n):
                while stack and nums[stack[-1]] > nums[i]: # either >= or > will work here
                    idx = stack.pop()
                    ans[idx][1] = i
                ans[i][0] = -1 if not stack else stack[-1]
                stack.append(i)
            return ans
        
        min_bounds_lookup = minimum_boundaries(arr)
        ans = 0
        MOD = 10 ** 9 + 7
        
        for i in range(len(arr)):
            left_boundary, right_boundary = min_bounds_lookup[i]
            num_subarrays = (i - left_boundary) * (right_boundary - i)
            contribution = arr[i] * num_subarrays
            ans += contribution
            
        return ans % MOD

LC 2104. Sum of Subarray Ranges

You are given an integer array nums. The range of a subarray of nums is the difference between the largest and smallest element in the subarray.

Return the sum of all subarray ranges of nums.

A subarray is a contiguous non-empty sequence of elements within an array.

This is a tough problem. It becomes much easier to solve after fully understanding the performant way to solve the following very similar problem (which is comprehensively dissected in this post's epilogue): LC 907. Sum of Subarray Minimums.

The optimized solution in Approach 1 directly stems from the discussion in the epilogue. Approach 2, which is arguably a good bit easier to come up with, stems from the discussion in the last bullet point of the important observations section (i.e., the bullet point right above the monotonic stack definition).

Approach 1

class Solution:
    def subArrayRanges(self, nums: List[int]) -> int:
        n = len(nums)
        stack = []
        total_subarray_minimum_sum = 0
        total_subarray_maximum_sum = 0
        
        # calculate total contribution of subarray minimums
        for i in range(n + 1):
            while stack and (i == n or nums[stack[-1]] >= nums[i]): # note: either '>=' or '>' can be used
                curr_min_idx = stack.pop()
                curr_min = nums[curr_min_idx]
                left_boundary = -1 if not stack else stack[-1]
                right_boundary = i
                num_subarrays = (curr_min_idx - left_boundary) * (right_boundary - curr_min_idx)
                contribution = curr_min * num_subarrays
                total_subarray_minimum_sum += contribution
            stack.append(i)
        
        # reset the stack
        stack = []
        
        # calculate total contribution of subarray maximums
        for i in range(n + 1):
            while stack and (i == n or nums[stack[-1]] <= nums[i]): # note: either '<=' or '<' can be used
                curr_max_idx = stack.pop()
                curr_max = nums[curr_max_idx]
                left_boundary = -1 if not stack else stack[-1]
                right_boundary = i
                num_subarrays = (curr_max_idx - left_boundary) * (right_boundary - curr_max_idx)
                contribution = curr_max * num_subarrays
                total_subarray_maximum_sum += contribution
            stack.append(i)
            
        return total_subarray_maximum_sum - total_subarray_minimum_sum

Approach 2

class Solution:
    def subArrayRanges(self, nums: List[int]) -> int:
        def minimum_boundaries(nums):
            n = len(nums)
            # missing previous values assigned as -1 (just before leftmost boundary)
            # missing next values assigned as n (just after rightmost boundary)
            ans = [[-1, n] for _ in range(n)]
            stack = [] # monotonic stack
            
            # the comparison operator (?) dictates what each element's PREVIOUS and NEXT values will be
            # (>=) PREVIOUS smaller value and NEXT smaller or equal value (strictly increasing stack)
            #       (good for finding minimums, non-strict to left and strict to right)
            # (>)  PREVIOUS smaller or equal value and NEXT smaller value (weakly increasing stack)
            #       (good for finding minimums, strict to left and non-strict to right)
            for i in range(n):
                while stack and nums[stack[-1]] > nums[i]: # either >= or > will work here
                    idx = stack.pop()
                    ans[idx][1] = i
                ans[i][0] = -1 if not stack else stack[-1]
                stack.append(i)
            return ans

        def maximum_boundaries(nums):
            n = len(nums)
            # missing previous values assigned as -1 (just before leftmost boundary)
            # missing next values assigned as n (just after rightmost boundary)
            ans = [[-1, n] for _ in range(n)]
            stack = [] # monotonic stack
            
            # the comparison operator (?) dictates what each element's PREVIOUS and NEXT values will be
            # (<=) PREVIOUS larger value and NEXT larger or equal value (strictly decreasing stack)
            #       (good for finding maximums, non-strict to left and strict to right)
            # (<)  PREVIOUS larger or equal value and NEXT larger value (weakly decreasing stack)
            #       (good for finding maximums, strict to left and non-strict to right)
            for i in range(n):
                while stack and nums[stack[-1]] < nums[i]: # either <= or < will work here
                    idx = stack.pop()
                    ans[idx][1] = i
                ans[i][0] = -1 if not stack else stack[-1]
                stack.append(i)
            return ans
        
        min_bounds_lookup = minimum_boundaries(nums)
        max_bounds_lookup = maximum_boundaries(nums)
        ans = 0
        
        for i in range(len(nums)):
            min_left_boundary, min_right_boundary = min_bounds_lookup[i]
            max_left_boundary, max_right_boundary = max_bounds_lookup[i]
            num_min_subarrays = (i - min_left_boundary) * (min_right_boundary - i)
            num_max_subarrays = (i - max_left_boundary) * (max_right_boundary - i)
            contribution = nums[i] * num_max_subarrays - nums[i] * num_min_subarrays
            ans += contribution
            
        return ans

Epilogue: Sum of subarray minimums and subarray ranges

Final boss battle! The following two problems, where the second one is effectively an extension of the first, can be solved using monotonic stacks:

The optimal solutions are a bit more sophisticated than some of the solutions we've explored so far in the practice problems. But that's okay. Let's cover some "prerequisite" content and then build out a solution to the first problem. Building out a solution to the second problem will then be rather simple.

Prerequisites

A few prerequisites will be helpful before crafting our solution to the first problem, LC 907. Sum of Subarray Minimums. Each prerequisite is thoroughly explained, but a TLDR is provided for those who just want a quick summary.

Counting subarrays

TLDR

An $n$ -element array has a total of $n(n+1)/2$ subarrays. If an array contains the value X and sub_1 = [..., X] is $m$ units long and sub_2 = [X, ...] is $n$ units long, then combining sub_1 and sub_2 at value X results in another subarray, sub_3, that is $m + n - 1$ units long. How many subarrays of sub_3 include the value X? Answer: $mn$ .

How many subarrays are there for an $n$ -element array? There are $n(n+1)/2$ . Why? Consider the following range of index values: [left, right] (i.e., left == 0 and right == n - 1). How many subarrays end at left? A single one, the following one-element subarray (this is an index range): [left, left]. How many subarrays end at [left + 1]? We would have subarrays with index ranges [left + 1, left + 1] and [left, left + 1] (i.e., 2 such subarrays). In general:

index       subarrays ending at this index
--------------------------------------------
left        -> 1
left + 1    -> 2
left + 2    -> 3
right - 1   -> n - 1
right       -> n

That is, an $n$ -element array has $1 + 2 + \cdots + (n-1) + n = n(n+1)/2$ subarrays (see this formula for recalling how to sum the first $n$ positive integers).

How does the information above help in solving LC 907. Sum of Subarray Minimums? It helps because of how we can now consider an array with two adjacent subarrays where these subarrays share a single value, $X$ :

[a, b, c, \ldots, X, \ldots, y, z]

Suppose the first subarray, $[c, \ldots, X]$ , is $m$ units long, and the second subarray, $[X, \ldots, y, z]$ , is $n$ units long. How many subarrays in total would there be for the combined array of length $m + n - 1$ (we subtract 1 because of the de-deuplicated $X$ -value): $[c, \ldots, X, \ldots, y, z]$ . From the formula above, we would have the following:

\frac{(m + n - 1)[(m + n - 1) + 1]}{2} = \frac{(m + n)(m + n - 1)}{2}.

But suppose we're only interested in subarrays that contain $X$ . How many such subarrays would there be?

The subarray $[c, \ldots, X]$ is $m$ units long, which means $[c, \ldots, X]$ without $X$ would be $m-1$ units long (the rightmost element is excluded). Hence, there would be $(m-1)[(m-1)+1]/2=m(m-1)/2$ subarrays without $X$ .
The subarray $[X, \ldots, y, z]$ is $n$ units long, which means $[X, \ldots, y, z]$ without $X$ would be $n-1$ units long (the leftmost element is excluded). Hence, there would be $(n-1)[(n-1)+1]/2=n(n-1)/2$ subarrays without $X$ .

Thus, the total number of subarrays in $[c, \ldots, X, \ldots, y, z]$ that must contain $X$ is as follows:

\begin{align*} \mathrm{Total} &= \underbrace{\overbrace{\frac{(m + n)(m + n - 1)}{2}}^{\text{total number of subarrays}} - \overbrace{\frac{m(m-1)}{2}}^{\text{subarrays without ${\footnotesize X}$}} - \overbrace{\frac{n(n-1)}{2}}^{\text{subarrays without ${\footnotesize X}$}}}_{\text{subarrays with ${\footnotesize X}$ included}}\\[3em] &= \frac{m^2 + mn - m + mn + n^2 - n}{2} - \frac{m^2 - m}{2} - \frac{n^2 - n}{2} & \text{(distribute)}\\[1em] &= \frac{m^2 + mn - m + mn + n^2 - n - m^2 + m - n^2 + n}{2} & \text{(simplify)}\\[1em] &= \frac{2mn}{2} & \text{(simplify)}\\[1em] &= mn \end{align*}

There's actually a much easier way of getting to this result: use the fundamental principle of counting! For $X$ to be included in all subarrays, our subarray must first start with a value in $[c, \ldots, X]$ and end with a value in $[X, \ldots, y, z]$ ; that is, if our subarray starts with a value in $[c, \ldots, X]$ and ends with a value in $[X, \ldots, y, z]$ , then how would it be possible for $X$ to not be included? It wouldn't be possible.

How many choices do we have so that our subarray starts with an element from the $m$ -element subarray $[c, \ldots, X]$ ? We'd have $m$ choices. How many choices do we have so that our subarray ends with an element from the $n$ -element subarray $[X, \ldots, y, z]$ ? We'd have $n$ choices. Thus, there are $m\times n = mn$ possibilities for subarrays where the first element is from $[c, \ldots, X]$ and the last element is from $[X, \ldots, y, z]$ . This means there are $mn$ subarrays of $[c, \ldots, X, \ldots, y, z]$ that must include $X$ .

Excluding endpoints of subarrays

TLDR

If the open interval (L, R) is to fully represent an array, nums, with n elements, then L should be -1 at a minimum and R should be n at a maximum. This ensures all index values of nums, namely [0,1,...,n-2,n-1], fit within the open interval (-1, n).

The interval notations $[a,b]$ , $(a,b)$ , $(a,b]$ , and $[a, b)$ mean the following, respectively: $a$ and $b$ are both included, $a$ and $b$ are both excluded, $a$ is excluded but $b$ is included, and $a$ is included but $b$ is excluded.

Suppose we're given an integer array nums that contains n unique values. Then [0,1,...,n-2,n-1] represents the possible indexes. Suppose we know a value X occurs in nums, and we'd like to know how many subarrays there are where X is the minimum value. Then one way of approaching this is to find the indexes of the first values that occur before and after X, say L and R, such that both of these values are less than X. For example, suppose X = 3, and we're given the array [2,1,6,3,4,5,0]. We can find appropriate values for L and R as follows (indexes are drawn above the array elements for clarification)

     L     X        R
  0  1  2  3  4  5  6
[ 2  1  6  3  4  5  0 ]

Then the subarray contained in (L, R) has X = 3 as its minimum value: (L, R) = [L + 1, R - 1] = [6, 3, 4, 5]. How many subarrays of [6, 3, 4, 5] have 3 as their minimum value? We can methodically answer this question as follows:

How many subarrays are there in total for an array with four elements? There are $4(4+1)/2 = 10$ subarrays. How many of these contain the minimum value of 3? We're basically asking the question we asked in the previous section where the subarray [6, 3, 4, 5] may be viewed as joining two subarrays at the common value of 3: [6, 3] and [3, 4, 5]. How many subarrays are there where 3 must be included?
How many ways are there so our subarray including 3 starts with an element from [6, 3]? There are two elements so the answer is 2.
How many ways are there so our subarray including 3 ends with an element from [3, 4, 5]? There are three elements so the answer is 3.

Thus, there are 2 * 3 = 6 subarrays of [6, 3, 4, 5] where 3 is included. For the sake of completeness, the following are the 10 - 6 = 4 subarrays where 3 is not included: [6], [4], [5], and [4, 5]. All other subarrays include 3, where 3 is the minimum value.

Note that we could have obtained the values of 2 and 3 in the last two bullet points above by directly using the excluded endpoints, L and R, in relation to the index of the minimum value of interest, namely 3, which occurs at index 3. Let i denote the index of where value X occurs (i.e., i = 3 for the example we've been considering). Then we have the following:

i - L = 3 - 1 = 2
R - i = 6 - 3 = 3

That's great but what if X occurs at one of the endpoints? For example, what if X occured at i = 0 or i = 6 in the example above (i.e., X = 2 or X = 0, respectively)? Then what should the values of L and R be? They should be -1 and n = len(nums) == 7, respectively:

-1 
 L  X  R
    0  1  2  3  4  5  6
  [ 2  1  6  3  4  5  0 ]


-1                       7
 L                    X  R
    0  1  2  3  4  5  6
  [ 2  1  6  3  4  5  0 ]

When X = 2, we would then have the following:

i - L = 0 - (-1) = 1
R - i = 1 - 0 = 1

We're basically asking how many subarrays of [2] there are where 2 is the minimum value. There are 1 * 1 = 1 such subarrays because there is only one way our subarray can start with a value from [2] and only one way our subarray can end with a value from [2].

When X = 0, we would then have the following:

i - L = 6 - (-1) = 7
R - i = 7 - 6 = 1

We're basically asking how many subarrays of [2, 1, 6, 3, 4, 5, 0] there are where 0 is the minimum value. There are 7 * 1 = 7 such subarrays because there are seven ways our subarray can start with a value from [2, 1, 6, 3, 4, 5, 0] and only one way our subarray can end with a value from [0].

The entire discussion above suggests we should let L = -1 and/or R = len(nums) if either (or both) endpoint does not exist for a given value of interest, X.

Subarrays with non-unique minimums and maximums

TLDR

We must be careful when considering minimum and maximum values of subarrays where these values occur more than once. Specifically, the current value we consider to be a minimum or maximum, curr_min_or_max, should be as far left or as far right as possible to ensure subsequently encountered values that are equivalent to curr_min_or_max are handled appropriately (i.e., not overcounted).

Given the input array [2,1,6,3,4,5,0], how many subarrays have 3 as their minimum value? The previous section showed this number to be 6. What if, however, we're given an input array with non-unique values? This complicates things. For example, consider the following array of values: [3, 4, 4, 5, 4, 1]. How many times does each value serve as the minimum for a subarray? Calculating this shouldn't be too difficult for the unique values of 3, 5, and 1 by using the technique described in the previous section. But the non-unique values of 4 present an issue. We need to make sure we do not overcount by counting more than once a subarray where 4 is the minimum value. What should we do? We need a strategy for somehow processing the non-unique values so that each contribution is distinctly its own. In the strategies presented below, we are always trying to find how many times the current value being processed (the one with i above it) should be considered the minimum of a subarray (the same concept applies for maximum values).

As our first consideration, suppose we were strict in not permitting non-unique values to be part of the subarray contribution for which the current value is the minimum (by "strict" we mean not allowing a value to be in the subarray that is equal to the current value serving as the minimum):

STRICT (to left and to right)
    i                   |       i                |          i             |
    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |
  [[3] 4  4  5  4  1 ]  |  [ 3 [4] 4  5  4  1 ]  |  [ 3  4 [4] 5  4  1 ]  |

It's clear we've already run into an issue as soon as we reach the value at index i = 2: we entirely skipped the subarray [4, 4] where 4 is a minimum value. This is clearly not a viable strategy. What if we indiscriminately allowed duplicate values? Then our consideration would effectively be "non-strict both ways":

NON-STRICT (to left and to right)
    i                   |       i                |          i             |
    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |
  [[3] 4  4  5  4  1 ]  |  [ 3 [4] 4  5  4  1 ]  |  [ 3  4 [4] 5  4  1 ]  |
                        |  [ 3 [4  4] 5  4  1 ]  |  [ 3 [4  4] 5  4  1 ]  |
                        |  [ 3 [4  4  5] 4  1 ]  |
                        |  [ 3 [4  4  5  4] 1 ]  |

This is also not a viable strategy because, as the highlighted line above demonstrates, we've now counted the subarry [4, 4] twice as having the minimum value of 4. What if instead of imposing strict or non-strict inclusion conditions in both directions (to left and to right), we tried imposing a strict condition in one direction and a non-strict condition in the other (i.e., non-strict to left and strict to right or strict to left and non-strict to right)? Let's see:

NON-STRICT (to left) and STRICT (to right)
    i                   |       i                |          i             |             i          |                i       |                   i    |
    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |
  [[3] 4  4  5  4  1 ]  |  [ 3 [4] 4  5  4  1 ]  |  [ 3  4 [4] 5  4  1 ]  |  [ 3  4  4 [5] 4  1 ]  |  [ 3  4  4  5 [4] 1 ]  |  [ 3  4  4  5  4 [1]]  |
  [[3  4] 4  5  4  1 ]  |                        |  [ 3 [4  4] 5  4  1 ]  |                        |  [ 3  4  4 [5  4] 1 ]  |  [ 3  4  4  5 [4  1]]  |
  [[3  4  4] 5  4  1 ]  |                        |  [ 3  4 [4  5] 4  1 ]  |                        |  [ 3  4 [4  5  4] 1 ]  |  [ 3  4  4 [5  4  1]]  |
  [[3  4  4  5] 4  1 ]  |                        |  [ 3 [4  4  5] 4  1 ]  |                        |  [ 3 [4  4  5  4] 1 ]  |  [ 3  4 [4  5  4  1]]  |
  [[3  4  4  5  4] 1 ]  |                        |                        |                        |                        |  [ 3 [4  4  5  4  1]]  |
                        |                        |                        |                        |                        |  [[3  4  4  5  4  1]]  |

Were any subarrays overcounted? How many subarrays are there for an array with six elements? There are $6(6+1)/2 =21$ subarrays. How many subarrays are illustrated above? There are, pictured from left to right, $5 + 1 + 4 + 1 + 4 + 6 = 21$ subarrays, where each i value represents the index of the minimum value for each subarray in its designated block.

For the sake of completeness, let's also consider tabulating subarrays in a "strict to left and non-strict to right" fashion:

STRICT (to left) and NON-STRICT (to right)
    i                   |       i                |          i             |             i          |                i       |                   i    |
    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |
  [[3] 4  4  5  4  1 ]  |  [ 3 [4] 4  5  4  1 ]  |  [ 3  4 [4] 5  4  1 ]  |  [ 3  4  4 [5] 4  1 ]  |  [ 3  4  4  5 [4] 1 ]  |  [ 3  4  4  5  4 [1]]  |
  [[3  4] 4  5  4  1 ]  |  [ 3 [4  4] 5  4  1 ]  |  [ 3  4 [4  5] 4  1 ]  |                        |  [ 3  4  4 [5  4] 1 ]  |  [ 3  4  4  5 [4  1]]  |
  [[3  4  4] 5  4  1 ]  |  [ 3 [4  4  5] 4  1 ]  |  [ 3  4 [4  5  4] 1 ]  |                        |                        |  [ 3  4  4 [5  4  1]]  |
  [[3  4  4  5] 4  1 ]  |  [ 3 [4  4  5  4] 1 ]  |                        |                        |                        |  [ 3  4 [4  5  4  1]]  |
  [[3  4  4  5  4] 1 ]  |                        |                        |                        |                        |  [ 3 [4  4  5  4  1]]  |
                        |                        |                        |                        |                        |  [[3  4  4  5  4  1]]  |

This also looks very promising. The number of subarrays, pictured left to right, are as follows: $5 + 4 + 3 + 1 + 2 + 6 = 21$ .

How are the two viable approaches above qualitatively different from each other? They both seem to achieve the same outcome in different ways. If we look closely, we can see that unique minimum values (i.e., 3, 5, and 1 in [3,4,4,5,4,1]) are handled in exactly the same way. The difference simply lies in how we handle non-unique values (i.e., the 4 in the examples above). Both approaches count the correct number of subarrays, but they simply do so in different ways. The takeaway is that we should handle values in a strict way in one direction and a non-strict way in the other direction. Which ways we choose for strict/non-strict inclusion is immaterial and does not alter the overall desired result.

LC 907. Sum of Subarray Minimums (approach 1)

We're finally ready to work on crafting a solution to LC 907! Here's the problem statement:

Given an array of integers arr, find the sum of min(b), where b ranges over every (contiguous) subarray of arr. Since the answer may be large, return the answer modulo 10⁹ + 7.

As noted in the section immediately above, to effectively handle duplicate values, which this problem allows, we must consider strictness in one direction and non-strictness in the other direction. Furthermore, we can make the following observations from the last two examples in the section above:

NON-STRICT (to left) and STRICT (to right): Non-strict to the left means values to the left of the value being considered the minimum may be repeated; hence, the left boundary should be the minimum value's previous smaller value if it exists (or -1 if it does not, as noted in the section on endpoints). Strict to the right means the right boundary should be the minimum value's next smaller or equal value if it exists (or len(nums) if it does not) because smaller or equal values may not be included in the subarray of the value we're considering to be the minimum.

Note that this suggests we can use the previous value and next value templates to good effect here. Specifically, each minimum's left boundary may be found by using the >= comparison operator in the previous value template (this gives us each value's previous smaller value or -1 if no such value exists). Each minimum's right boundary may be found by using the >= comparison operator in the next value template (this gives us each value's next smaller or equal value or len(arr) if no such value exists).

Solution 1 (non-strict to left and strict to right)

class Solution:
    def sumSubarrayMins(self, arr: List[int]) -> int:
        def previous_less(nums):
            n = len(nums)
            ans = [None] * n
            stack = []
            
            for i in range(n):
                val_A = nums[i]
                while stack and nums[stack[-1]] >= val_A:
                    stack.pop()
                    
                if stack:
                    ans[i] = stack[-1]
                else:
                    ans[i] = -1
                    
                stack.append(i)
                    
            return ans

        def next_less_or_equal(nums):
            n = len(nums)
            ans = [None] * n
            stack = []
            
            for i in range(n):
                val_B = nums[i]
                while stack and nums[stack[-1]] >= val_B:
                    idx_val_A = stack.pop()
                    ans[idx_val_A] = i
                stack.append(i)
            
            while stack:
                idx_val_A = stack.pop()
                ans[idx_val_A] = n
                
            return ans
        
        # assemble the left and right boundaries for each value
        left_boundaries = previous_less(arr)
        right_boundaries = next_less_or_equal(arr)
        
        MOD = 10 ** 9 + 7
        ans = 0
        for i in range(len(arr)):
            curr_min = arr[i]
            left_boundary = left_boundaries[i]
            right_boundary = right_boundaries[i]
            num_subarrays = (i - left_boundary) * (right_boundary - i)
            contribution = curr_min * num_subarrays
            ans += contribution
            
        return ans % MOD

STRICT (to left) and NON-STRICT (to right): Strict to the left means values to the left of the value being considered the minimum may not be repeated; hence, the left boundary should be the minimum value's previous smaller or equal value if it exists (or -1 if it does not, as noted in the section on endpoints). Non-strict to the right means the right boundary should be the minimum value's next smaller value if it exists (or len(nums) if it does not).

Note that this suggests we can use the previous value and next value templates to good effect here. Specifically, each minimum's left boundary may be found by using the > comparison operator in the previous value template (this gives us each value's previous smaller or equal value or -1 if no such value exists). Each minimum's right boundary may be found by using the > comparison operator in the next value template (this gives us each value's next smaller value or len(arr) if no such value exists).

Solution 2 (strict to left and non-strict to right)

class Solution:
    def sumSubarrayMins(self, arr: List[int]) -> int:
        def previous_less_or_equal(nums):
            n = len(nums)
            ans = [None] * n
            stack = []
            
            for i in range(n):
                val_A = nums[i]
                while stack and nums[stack[-1]] > val_A:
                    stack.pop()
                    
                if stack:
                    ans[i] = stack[-1]
                else:
                    ans[i] = -1
                    
                stack.append(i)
                    
            return ans

        def next_less(nums):
            n = len(nums)
            ans = [None] * n
            stack = []
            
            for i in range(n):
                val_B = nums[i]
                while stack and nums[stack[-1]] > val_B:
                    idx_val_A = stack.pop()
                    ans[idx_val_A] = i
                stack.append(i)
            
            while stack:
                idx_val_A = stack.pop()
                ans[idx_val_A] = n
                
            return ans

        # assemble the left and right boundaries for each value
        left_boundaries = previous_less_or_equal(arr)
        right_boundaries = next_less(arr)
        
        MOD = 10 ** 9 + 7
        ans = 0
        for i in range(len(arr)):
            curr_min = arr[i]
            left_boundary = left_boundaries[i]
            right_boundary = right_boundaries[i]
            num_subarrays = (i - left_boundary) * (right_boundary - i)
            contribution = curr_min * num_subarrays
            ans += contribution
            
        return ans % MOD

Both solutions above are valid and completely follow from all the prerequisite work we did. Try submitting the solutions on LeetCode for yourself!

LC 907. Sum of Subarray Minimums (approach 2, beast mode)

The approach outlined above for solving LC 907 is great in that it is somewhat intuitive (but only after doing a lot of work to get to that point). Nonetheless, it is possible to get even more creative and come up with a solution that requires only a single full pass. Our solution in the previous approach required three full passes: one to find the left boundaries, one to find the right boundaries, and then one to calculate what the contribution of each minimum value was to the overall answer.

But note how we used the same comparison operator in the previous and next value templates in the solution variations in our previous approach: we used >= for the "non-strict to left and strict to right" solution and > for the "strict to left and non-strict to right" solution. Comparisons using >= and > (and even those using <= and <) naturally divide elements in a "strict" and "non-strict" way. Perhaps there's a way to compress our logic a bit and come up with an "ultimately optimized" solution. To do this, let's first recall the "next value" problem template in its entirety:

Next value problem template

def fn(nums):
    n = len(nums)
    ans = [None] * n
    stack = [] # monotonic stack
    for i in range(n):
        val_B = nums[i]
        # the comparison operator (?) dictates what A's next value B represents
        # (<)  next larger value (weakly decreasing stack)
        # (<=) next larger or equal value (strictly decreasing stack)
        # (>)  next smaller value (weakly increasing stack)
        # (>=) next smaller or equal value (strictly increasing stack)
        while stack and nums[stack[-1]] ? val_B:
            idx_val_A = stack.pop()
            ans[idx_val_A] = val_B
        stack.append(i)
    
    # process elements that never had a "next" value that satisfied the criteria
    while stack:
        idx_val_A = stack.pop()
        ans[idx_val_A] = -1
    
    return ans

Can this template be used for more than just identifying a given value's "next larger/smaller (or equal)" value? Specifically, is there a way we can use it to count the number of subarrays for which each value serves as the minimum or maximum value (even when the min/max of a subarray may not be unique)? The manner in which we are maintaining the stack for each comparison operator suggests this may be possible (even though this is not at all obvious at first). Creativity and insight are needed. The key lies in thinking about how each item popped from the top of the stack, val_A, relates to its previous and next values (note: by val_A we mean val_A = nums[idx_val_A] since the stack holds index values):

The next value for val_A is val_B, the value referenced by the current for loop iteration (line 6).
The previous value for val_A is prev_A, a value that does not appear in the template above. Why? Because the template made no use of this value previously (so it was not necessary). By prev_A we mean the new value at the top of the stack once val_A has been popped (after line 13). If, however, the stack is empty after val_A has been popped, then this means val_A has no previous value that can be related to it in the way that previously encountered values lower in the stack could.

Before analyzing how these relations work for each comparison operator, it's important to consider how values should be handled that have no "next value" that satisfies our criteria. In the template, lines 18-20 specify that a value of -1 should be assigned to the answer array for such values; that is, ans[i] == -1 would mean nums[i] had no next value that satisfied our criteria. But we do not have to use -1. We should use whatever value makes the most sense under the circumstances. Note that, under the current circumstances, we also need to consider how we should convey that prev_A does not exist for val_A when this is the case (i.e., when the stack is empty after popping val_A on line 13).

What values make the most sense under the circumstances? The "circumstance" here is the context of working with open intervals such as (L, R), where L and R refer to excluded left and right boundaries, respectively (where L and R are index values). Our previous work indicates we should let L = -1 and R = len(nums) when no previous or next value is found that meets the specified criteria, respectively.

Other key ideas that apply regardless of comparison operator being used (what each choice actually entails in terms of the behavior observed is, however, specific to the comparison operator being used):

Min/max value (curr_min_max): This will always be the value popped from the stack: curr_min_max = nums[stack[-1]]. Our goal is to answer the following question: "How many subarrays are there for which curr_min_max is the subarray's minimum or maximum?"
Left boundary (left_boundary): This will always be the value at the top of the stack after we've popped the value we're treating as the minimum or maximum (if the stack is non-empty); if, however, the stack is empty after popping what we're considering to be the minimum or maximum value, then -1 will be assigned as the left boundary.
Right boundary (right_boundary): This will always be the index of the current for loop iteration (or len(input_array) if no constraint-specific "next value" is found).

Comparison operator: >= (good for finding minimums, non-strict to left and strict to right)

The >= comparison used in the condition nums[stack[-1]] >= nums[i] for the while loop implies the following:

curr_min: How many subarrays have curr_min = nums[stack[-1]] as their minimum value?
left_boundary: If the stack is empty, then curr_min has no previous smaller value and -1 is the left boundary. If the stack is non-empty, then stack[-1] points to curr_min's previous smaller value.
right_boundary: i is the right boundary and nums[i] is curr_min's next smaller than or equal value (or len(nums) if no such next smaller or equal value exists).

The information above translates as follows in terms of the boundary behavior we can expect of our subarrays:

nums[left_boundary] < curr_min, hence the half-open interval (nums[left_boundary], ... , curr_min] could include duplicate values of curr_min. Since nums[left_boundary] refers to curr_min's previous smaller value (as opposed to previous smaller or equal value) there may be any number of other values equal to curr_min that appear before the curr_min we're considering, namely curr_min = nums[stack[-1]]. This means any of the other duplicate values would all lie to the left of our curr_min.
curr_min >= nums[right_boundary], hence the half-open interval [curr_min, ..., nums[right_boundary]) cannot include any duplicate values of curr_min because the right boundary is excluded.

In regards to curr_min = nums[stack[-1]], our minimum, we can effectively envision the subarrays that have this value as their minimum as being "non-strict to the left" (where other values equal to curr_min may be included) and "strict to the right" (where other values equal to curr_min may not be included). This demonstrates why we do not need to be worried about overcounting subarray minimum contributions when duplicate values of curr_min are included: we only ever consider subarrays that include the curr_min farthest to the right.

The following example illustrates the mechanics for the input array nums = [3, 4, 4, 5, 4, 1]:

NON-STRICT TO LEFT, STRICT TO RIGHT:

- Left boundary is SMALLER than curr_min (i.e., nums[L] < nums[i] or L == -1 if no such value exists)
- Right boundary is SMALLER OR EQUAL to curr_min (i.e., nums[R] <= nums[i] or R == len(nums) if no such value exists)

-1                                                                                                                           -1                    6
 L  i              R    |    L  i  R             |    L     i     R       |          L  i  R       |    L           i  R    | L                 i  R |
    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |
  [[3] 4  4  5  4  1 ]  |  [ 3 [4] 4  5  4  1 ]  |  [ 3  4 [4] 5  4  1 ]  |  [ 3  4  4 [5] 4  1 ]  |  [ 3  4  4  5 [4] 1 ]  |  [ 3  4  4  5  4 [1]]  |
  [[3  4] 4  5  4  1 ]  |                        |  [ 3 [4  4] 5  4  1 ]  |                        |  [ 3  4  4 [5  4] 1 ]  |  [ 3  4  4  5 [4  1]]  |
  [[3  4  4] 5  4  1 ]  |                        |  [ 3  4 [4  5] 4  1 ]  |                        |  [ 3  4 [4  5  4] 1 ]  |  [ 3  4  4 [5  4  1]]  |
  [[3  4  4  5] 4  1 ]  |                        |  [ 3 [4  4  5] 4  1 ]  |                        |  [ 3 [4  4  5  4] 1 ]  |  [ 3  4 [4  5  4  1]]  |
  [[3  4  4  5  4] 1 ]  |                        |                        |                        |                        |  [ 3 [4  4  5  4  1]]  |
                        |                        |                        |                        |                        |  [[3  4  4  5  4  1]]  |

subarray count = [(0 - (-1)) * (5 - 0)] + [(1 - 0) * (2 - 1)] + [(2 - 0) * (4 - 2)] + [(3 - 2) * (4 - 3)] + [(4 - 0) * (5 - 4)] + [(5 - (-1)) * (6 - 5)]
               = 5 + 1 + 4 + 1 + 4 + 6 = 21

subarray sum of maximums = (3 * 5) + (4 * 1) + (4 * 4) + (5 * 1) + (4 * 4) + (1 * 6)
                         = 15 + 4 + 16 + 5 + 16 + 6
                         = 62

Comparison operator: > (good for finding minimums, strict to left and non-strict to right)

The > comparison used in the condition nums[stack[-1]] > nums[i] for the while loop implies the following:

curr_min: How many subarrays have curr_min = nums[stack[-1]] as their minimum value?
left_boundary: If the stack is empty, then curr_min has no previous smaller or equal value and -1 is the left boundary. If the stack is non-empty, then stack[-1] points to curr_min's previous smaller or equal value.
right_boundary: i is the right boundary and nums[i] is curr_min's next smaller value (or len(nums) if no such next smaller value exists).

The information above translates as follows in terms of the boundary behavior we can expect of our subarrays:

nums[left_boundary] <= curr_min, where nums[left_boundary] is curr_min's previous smaller or equal value. If nums[left_boundary] is equal to curr_min, then this means these values are adjacent in whatever subarrays we're considering for which curr_min = nums[stack[-1]] is the minimum value.
curr_min > nums[right_boundary], which means duplicated values of curr_min may appear before nums[right_boundary], but if these values appear, then note that they all lie to the right of the curr_min we're considering to be the minimum, namely curr_min = nums[stack[-1]].

In regards to curr_min = nums[stack[-1]], our minimum, we can effectively envision the subarrays that have this value as their minimum as being "strict to the left" (where other values equal to curr_min may not be included) and "non-strict to the right" (where other values equal to curr_min may be included). This demonstrates why we do not need to be worried about overcounting subarray minimum contributions when duplicate values of curr_min are included: we only ever consider subarrays that include the curr_min farthest to the left.

The following example illustrates the mechanics for the input array nums = [3, 4, 4, 5, 4, 1]:

STRICT TO LEFT, NON-STRICT TO RIGHT:

- Left boundary is SMALLER OR EQUAL to curr_min (i.e., nums[L] <= nums[i] or L == -1 if no such value exists)
- Right boundary is SMALLER than curr_min (i.e., nums[R] < nums[i] or R == len(nums))

-1                                                                                                                           -1                    6
 L  i              R    |    L  i           R    |       L  i        R    |          L  i  R       |             L  i  R    | L                 i  R |
    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |
  [[3] 4  4  5  4  1 ]  |  [ 3 [4] 4  5  4  1 ]  |  [ 3  4 [4] 5  4  1 ]  |  [ 3  4  4 [5] 4  1 ]  |  [ 3  4  4  5 [4] 1 ]  |  [ 3  4  4  5  4 [1]]  |
  [[3  4] 4  5  4  1 ]  |  [ 3 [4  4] 5  4  1 ]  |  [ 3  4 [4  5] 4  1 ]  |                        |  [ 3  4  4 [5  4] 1 ]  |  [ 3  4  4  5 [4  1]]  |
  [[3  4  4] 5  4  1 ]  |  [ 3 [4  4  5] 4  1 ]  |  [ 3  4 [4  5  4] 1 ]  |                        |                        |  [ 3  4  4 [5  4  1]]  |
  [[3  4  4  5] 4  1 ]  |  [ 3 [4  4  5  4] 1 ]  |                        |                        |                        |  [ 3  4 [4  5  4  1]]  |
  [[3  4  4  5  4] 1 ]  |                        |                        |                        |                        |  [ 3 [4  4  5  4  1]]  |
                        |                        |                        |                        |                        |  [[3  4  4  5  4  1]]  |

subarray count = [(0 - (-1)) * (5 - 0)] + [(1 - 0) * (5 - 1)] + [(2 - 1) * (5 - 2)] + [(3 - 2) * (4 - 3)] + [(4 - 3) * (5 - 4)] + [(5 - (-1)) * (6 - (-1))]
               = 5 + 4 + 3 + 1 + 2 + 6 = 21

subarray sum of minimums = (3 * 5) + (4 * 4) + (4 * 3) + (5 * 1) + (4 * 2) + (1 * 6)
                         = 15 + 16 + 12 + 5 + 8 + 6
                         = 62

Comparison operator: <= (good for finding maximums, non-strict to left and strict to right)

The <= comparison used in the condition nums[stack[-1]] <= nums[i] for the while loop implies the following:

curr_max: How many subarrays have curr_max = nums[stack[-1]] as their maximum value?
left_boundary: If the stack is empty, then curr_max has no previous larger value and -1 is the left boundary. If the stack is non-empty, then stack[-1] points to curr_max's previous larger value.
right_boundary: i is the right boundary and nums[i] is curr_max's next larger than or equal value (or len(nums) if no such next larger or equal value exists).

The information above translates as follows in terms of the boundary behavior we can expect of our subarrays:

nums[left_boundary] > curr_max, hence the half-open interval (nums[left_boundary], ... , curr_max] could include duplicate values of curr_max. Since nums[left_boundary] refers to curr_max's previous larger value (as opposed to previous larger or equal value) there may be any number of other values equal to curr_max that appear before the curr_max we're considering, namely curr_max = nums[stack[-1]]. This means any of the other duplicate values would all lie to the left of our curr_max.
curr_max >= nums[right_boundary], hence the half-open interval [curr_max, ..., nums[right_boundary]) cannot include any duplicate values of curr_max because the right boundary is excluded.

In regards to curr_max = nums[stack[-1]], our maximum, we can effectively envision the subarrays that have this value as their maximum as being "non-strict to the left" (where other values equal to curr_max may be included) and "strict to the right" (where other values equal to curr_max may not be included). This demonstrates why we do not need to be worried about overcounting subarray maximum contributions when duplicate values of curr_max are included: we only ever consider subarrays that include the curr_max farthest to the right.

The following example illustrates the mechanics for the input array nums = [3, 4, 4, 5, 4, 1]:

NON-STRICT TO LEFT, STRICT TO RIGHT:

- Left boundary is LARGER than curr_max (i.e., nums[L] > nums[i] or L == -1 if no such value exists)
- Right boundary is LARGER OR EQUAL to curr_max (i.e., nums[R] >= nums[i] or R == len(nums) if no such value exists)

-1                       -1                       -1                       -1                    6                        6                        6
 L  i  R                | L     i  R             | L        i  R          | L           i        R |             L  i     R |                L  i  R |
    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |
  [[3] 4  4  5  4  1 ]  |  [ 3 [4] 4  5  4  1 ]  |  [ 3  4 [4] 5  4  1 ]  |  [ 3  4  4 [5] 4  1 ]  |  [ 3  4  4  5 [4] 1 ]  |  [ 3  4  4  5  4 [1]]  |
                        |  [[3  4] 4  5  4  1 ]  |  [ 3 [4  4] 5  4  1 ]  |  [ 3  4 [4  5] 4  1 ]  |  [ 3  4  4  5 [4  1]]  |                        |
                        |                        |  [[3  4  4] 5  4  1 ]  |  [ 3 [4  4  5] 4  1 ]  |                        |                        |
                        |                        |                        |  [[3  4  4  5] 4  1 ]  |                        |                        |
                        |                        |                        |  [ 3  4  4 [5  4  1 ]  |                        |                        |
                        |                        |                        |  [ 3  4  4 [5  4] 1 ]  |                        |                        |
                        |                        |                        |  [ 3  4  4 [5  4  1]]  |                        |                        |
                        |                        |                        |  [ 3  4 [4  5  4] 1 ]  |                        |                        |
                        |                        |                        |  [ 3 [4  4  5  4] 1 ]  |                        |                        |
                        |                        |                        |  [[3  4  4  5  4] 1 ]  |                        |                        |
                        |                        |                        |  [ 3  4 [4  5  4  1]]  |                        |                        |
                        |                        |                        |  [ 3 [4  4  5  4  1]]  |                        |                        |
                        |                        |                        |  [[3  4  4  5  4  1]]  |                        |                        |

subarray count = [(0 - (-1)) * (1 - 0)] + [(1 - (-1)) * (2 - 1)] + [(2 - (-1)) * (3 - 2)] + [(3 - (-1)) * (6 - 3)] + [(4 - 3) * (6 - 4)] + [(5 - 4) * (6 - 5)]
               = 1 + 2 + 3 + 12 + 2 + 1 = 21

subarray sum of maximums = (3 * 1) + (4 * 2) + (4 * 3) + (5 * 12) + (4 * 2) + (1 * 1)
                         = 3 + 8 + 12 + 60 + 8 + 1
                         = 92

Comparison operator: < (good for finding maximums, strict to left and non-strict to right)

The < comparison used in the condition nums[stack[-1]] < nums[i] for the while loop implies the following:

curr_max: How many subarrays have curr_max = nums[stack[-1]] as their maximum value?
left_boundary: If the stack is empty, then curr_max has no previous larger or equal value and -1 is the left boundary. If the stack is non-empty, then stack[-1] points to curr_min's previous larger or equal value.
right_boundary: i is the right boundary and nums[i] is curr_max's next larger value (or len(nums) if no such next larger value exists).

The information above translates as follows in terms of the boundary behavior we can expect of our subarrays:

nums[left_boundary] >= curr_min, where nums[left_boundary] is curr_max's previous larger or equal value. If nums[left_boundary] is equal to curr_max, then this means these values are adjacent in whatever subarrays we're considering for which curr_max = nums[stack[-1]] is the maximum value.
curr_max > nums[right_boundary], which means duplicated values of curr_max may appear before nums[right_boundary], but if these values appear, then note that they all lie to the right of the curr_max we're considering to be the maximum, namely curr_max = nums[stack[-1]].

In regards to curr_max = nums[stack[-1]], our maximum, we can effectively envision the subarrays that have this value as their maximum as being "strict to the left" (where other values equal to curr_max may not be included) and "non-strict to the right" (where other values equal to curr_max may be included). This demonstrates why we do not need to be worried about overcounting subarray maximum contributions when duplicate values of curr_max are included: we only ever consider subarrays that include the curr_max farthest to the left.

The following example illustrates the mechanics for the input array nums = [3, 4, 4, 5, 4, 1]:

STRICT TO LEFT, NON-STRICT TO RIGHT

- Left boundary is LARGER OR EQUAL to curr_max (i.e., nums[L] >= nums[i] or L == -1 if no such value exists)
- Right boundary is LARGER than curr_max (i.e., nums[R] > nums[i] or R == len(nums) if no such value exists)

-1                       -1                                                -1                    6                        6                        6
 L  i  R                | L     i     R          |       L  i  R          | L           i        R |             L  i     R |                L  i  R |
    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |    0  1  2  3  4  5    |
  [[3] 4  4  5  4  1 ]  |  [ 3 [4] 4  5  4  1 ]  |  [ 3  4 [4] 5  4  1 ]  |  [ 3  4  4 [5] 4  1 ]  |  [ 3  4  4  5 [4] 1 ]  |  [ 3  4  4  5  4 [1]]  |
                        |  [[3  4] 4  5  4  1 ]  |                        |  [ 3  4 [4  5] 4  1 ]  |  [ 3  4  4  5 [4  1]]  |                        |
                        |  [ 3 [4  4] 5  4  1 ]  |                        |  [ 3 [4  4  5] 4  1 ]  |                        |                        |
                        |  [[3  4  4] 5  4  1 ]  |                        |  [[3  4  4  5] 4  1 ]  |                        |                        |
                        |                        |                        |  [ 3  4  4 [5  4  1 ]  |                        |                        |
                        |                        |                        |  [ 3  4  4 [5  4] 1 ]  |                        |                        |
                        |                        |                        |  [ 3  4  4 [5  4  1]]  |                        |                        |
                        |                        |                        |  [ 3  4 [4  5  4] 1 ]  |                        |                        |
                        |                        |                        |  [ 3 [4  4  5  4] 1 ]  |                        |                        |
                        |                        |                        |  [[3  4  4  5  4] 1 ]  |                        |                        |
                        |                        |                        |  [ 3  4 [4  5  4  1]]  |                        |                        |
                        |                        |                        |  [ 3 [4  4  5  4  1]]  |                        |                        |
                        |                        |                        |  [[3  4  4  5  4  1]]  |                        |                        |

subarray count = [(0 - (-1)) * (1 - 0)] + [(1 - (-1)) * (3 - 1)] + [(2 - 1) * (3 - 2)] + [(3 - (-1)) * (6 - 3)] + [(4 - 3) * (6 - 4)] + [(5 - 4) * (6 - 5)]
               = 1 + 4 + 1 + 12 + 2 + 1 = 21

subarray sum of maximums = (3 * 1) + (4 * 4) + (4 * 1) + (5 * 12) + (4 * 2) + (1 * 1)
                         = 3 + 16 + 4 + 60 + 8 + 1
                         = 92

Let's wire up a solution that uses the >= comparison operator (i.e., non-strict to left and strict to right) and iteratively improve on how we express this solution. If we use notation to reflect the language used in the discussions above, then the following would be an acceptable solution:

Solution 1 (variables named to reflect narrative discussion)
class Solution:
    def sumSubarrayMins(self, arr: List[int]) -> int:
        n = len(arr)
        stack = []
        ans = 0
        MOD = 10 ** 9 + 7
        
        for i in range(n):
            val_B = arr[i]
            while stack and arr[stack[-1]] >= val_B:
                idx_val_A = stack.pop()
                val_A = arr[idx_val_A]
                prev_A = -1 if not stack else stack[-1]
                ans += val_A * (idx_val_A - prev_A) * (i - idx_val_A)
            stack.append(i)

        # process all values that did not have a next smaller or equal value
        while stack:
            idx_val_A = stack.pop()
            val_A = arr[idx_val_A]
            prev_A = -1 if not stack else stack[-1]
            ans += val_A * (idx_val_A - prev_A) * (n - idx_val_A)
            
        return ans % MOD

An easy way to improve on the solution above is to name the variables in a way more indicative of the roles they actually play in the solution. It may also be helpful to make explicit what the left and right boundaries are, how many subarrays are due to the current minimum, and the overall contribution of those subarrays to the running sum:

Solution 2 (better variable names)
class Solution:
    def sumSubarrayMins(self, arr: List[int]) -> int:
        n = len(arr)
        stack = []
        ans = 0
        MOD = 10 ** 9 + 7
        
        for i in range(n):
            next_smaller_or_equal_val = arr[i]
            while stack and arr[stack[-1]] >= next_smaller_or_equal_val:
                curr_min_idx = stack.pop()
                curr_min = arr[curr_min_idx]
                left_boundary = -1 if not stack else stack[-1] # index of previous smaller value (or -1 if no such value exists)
                right_boundary = i                             # index of next smaller or equal value
                num_subarrays = (curr_min_idx - left_boundary) * (right_boundary - curr_min_idx)
                contribution = curr_min * num_subarrays
                ans += contribution
            stack.append(i)

        # process all values that did not have a next smaller or equal value
        while stack:
            curr_min_idx = stack.pop()
            curr_min = arr[curr_min_idx]
            left_boundary = -1 if not stack else stack[-1]  # index of previous smaller value (or -1 if no such value exists)
            right_boundary = n                              # index of next smaller or equal value (n = len(arr) since no such value existed)
            num_subarrays = (curr_min_idx - left_boundary) * (right_boundary - curr_min_idx)
            contribution = curr_min * num_subarrays
            ans += contribution
            
        return ans % MOD

The solution above seems to be a decent improvement as far as variable naming is concerned, but there seems to be a lot of repeated logic being used in lines 21-28 (this closely mirrors the logic being performed in lines 10-17). Is there a way to clean this up effectively? The second while loop, on lines 21-28, only runs when the stack still holds values for which we never found a "next smaller or equal" value. We can cleverly fold this logic into the core while loop on lines 10-17 if we allow ourselves one more for loop iteration (and we handle it effectively):

Solution 3 (optimized non-strict to left and strict to right)
class Solution:
    def sumSubarrayMins(self, arr: List[int]) -> int:
        n = len(arr)
        stack = []
        ans = 0
        MOD = 10 ** 9 + 7
        
        for i in range(n + 1):
            while stack and (i == n or arr[stack[-1]] >= arr[i]):
                curr_min_idx = stack.pop()
                curr_min = arr[curr_min_idx]
                left_boundary = -1 if not stack else stack[-1]    # previous smaller value is always stack[-1] or -1 if it does not exist
                right_boundary = i                                # only equals n after first full pass and when stack is non-empty (values with no next less or equal value)
                num_subarrays = (curr_min_idx - left_boundary) * (right_boundary - curr_min_idx)
                contribution = curr_min * num_subarrays
                ans += contribution
            stack.append(i)
            
        return ans % MOD

Only cosmetic changes are needed if we want to provide the optimized strict to left and non-strict to right solution:

Solution 4 (optimized strict to left and non-strict to right)
class Solution:
    def sumSubarrayMins(self, arr: List[int]) -> int:
        n = len(arr)
        stack = []
        ans = 0
        MOD = 10 ** 9 + 7
        
        for i in range(n + 1):
            while stack and (i == n or arr[stack[-1]] > arr[i]):
                curr_min_idx = stack.pop()
                curr_min = arr[curr_min_idx]
                left_boundary = -1 if not stack else stack[-1]    # previous smaller or equal value is always stack[-1] or -1 if it does not exist
                right_boundary = i                                # only equals n after first full pass and when stack is non-empty (values with no next less)
                num_subarrays = (curr_min_idx - left_boundary) * (right_boundary - curr_min_idx)
                contribution = curr_min * num_subarrays
                ans += contribution
            stack.append(i)
            
        return ans % MOD

LC 2104. Sum of Subarray Ranges

Our previous work allows our solution(s) to LC 2104 to be short and sweet. First the problem statement:

You are given an integer array nums. The range of a subarray of nums is the difference between the largest and smallest element in the subarray.

Return the sum of all subarray ranges of nums.

A subarray is a contiguous non-empty sequence of elements within an array.

Given any subarray, note that its range will be the difference between its maximum value and its minimum value. This problem is almost the same as LC 907. Sum of Subarray Minimums except now we're trying to subtract all minimum subarray value contributions from all maximum subarray value contributions:

class Solution:
    def subArrayRanges(self, nums: List[int]) -> int:
        n = len(nums)
        stack = []
        total_subarray_minimum_sum = 0
        total_subarray_maximum_sum = 0
        
        # calculate total contribution of subarray minimums
        for i in range(n + 1):
            while stack and (i == n or nums[stack[-1]] >= nums[i]): # note: either '>=' or '>' can be used
                curr_min_idx = stack.pop()
                curr_min = nums[curr_min_idx]
                left_boundary = -1 if not stack else stack[-1]
                right_boundary = i
                num_subarrays = (curr_min_idx - left_boundary) * (right_boundary - curr_min_idx)
                contribution = curr_min * num_subarrays
                total_subarray_minimum_sum += contribution
            stack.append(i)
        
        # reset the stack
        stack = []
        
        # calculate total contribution of subarray maximums
        for i in range(n + 1):
            while stack and (i == n or nums[stack[-1]] <= nums[i]): # note: either '<=' or '<' can be used
                curr_max_idx = stack.pop()
                curr_max = nums[curr_max_idx]
                left_boundary = -1 if not stack else stack[-1]
                right_boundary = i
                num_subarrays = (curr_max_idx - left_boundary) * (right_boundary - curr_max_idx)
                contribution = curr_max * num_subarrays
                total_subarray_maximum_sum += contribution
            stack.append(i)
            
        return total_subarray_maximum_sum - total_subarray_minimum_sum

This would have been a much more difficult problem to solve performantly without all of our previous work.

Contents​

Next greater height​

Approach 0 (brute force)​

Approach 1 (right to left, single pass)​

Process description​

Code implementation​

Code implementation confirms process description​

Approach 2 (left to right, single pass)​

Process intuition​

Process description​

Code implementation​

Code implementation confirms process description​

Approach 3 (single pass, modified question)​

Modifed problem statement​

Modified solution​

LC 739. Daily Temperatures​

Problem statement​

Solution​

Sliding window minimum​

Problem statement​

False start​

Fixed start​

Code implementation​

Code implementation confirms process description​

LC 239. Sliding Window Maximum​

Problem statement​

Solution​

Monotonic stacks and queues (deques)​

Definition of "monotonic"​

Important observations due to "monotonic" definition​

Monotonic stack definition​

Monotonic queue (deque) definition​

Common use cases for monotonic stacks and deques​

Templates for finding an element's "next" or "previous" value based on monotonic invariant being maintained​

Common problem (with template): Find a value's "next" larger/smaller (or equal) value​

Next larger value​

Next larger or equal value​

Next smaller value​

Next smaller or equal value​

General template for "next value" problems​

Tabular summary​

Common problem (with template): Find a value's "previous" larger/smaller (or equal) value​

Previous larger value​

Previous larger or equal value​

Previous smaller value​

Previous smaller or equal value​

General template for "previous value" problems​

Tabular summary​

Common problems combined: In one pass, find each value's "next" AND "previous" value based on monotonic invariant​

Templates for generalized monotonic stacks and deques​

Monotonic stack​

Monotonic queue (deque)​

LeetCode practice problems​

Monotonic stacks​

Monotonic queues​

Solved practice problems​

Epilogue: Sum of subarray minimums and subarray ranges​

Prerequisites​

Counting subarrays​

Excluding endpoints of subarrays​

Subarrays with non-unique minimums and maximums​

LC 907. Sum of Subarray Minimums (approach 1)​

LC 907. Sum of Subarray Minimums (approach 2, beast mode)​

LC 2104. Sum of Subarray Ranges​

Contents

Next greater height

Approach 0 (brute force)

Approach 1 (right to left, single pass)

Process description

Code implementation

Code implementation confirms process description

Approach 2 (left to right, single pass)

Process intuition

Process description

Code implementation

Code implementation confirms process description

Approach 3 (single pass, modified question)

Modifed problem statement

Modified solution

LC 739. Daily Temperatures

Problem statement

Solution

Sliding window minimum

Problem statement

False start

Fixed start

Code implementation

Code implementation confirms process description

LC 239. Sliding Window Maximum

Problem statement

Solution

Monotonic stacks and queues (deques)

Definition of "monotonic"

Important observations due to "monotonic" definition

Monotonic stack definition

Monotonic queue (deque) definition

Common use cases for monotonic stacks and deques

Templates for finding an element's "next" or "previous" value based on monotonic invariant being maintained

Common problem (with template): Find a value's "next" larger/smaller (or equal) value

Next larger value

Next larger or equal value

Next smaller value

Next smaller or equal value

General template for "next value" problems

Tabular summary

Common problem (with template): Find a value's "previous" larger/smaller (or equal) value

Previous larger value

Previous larger or equal value

Previous smaller value

Previous smaller or equal value

General template for "previous value" problems

Tabular summary

Common problems combined: In one pass, find each value's "next" AND "previous" value based on monotonic invariant

Templates for generalized monotonic stacks and deques

Monotonic stack

Monotonic queue (deque)

LeetCode practice problems

Monotonic stacks

Monotonic queues

Solved practice problems

Epilogue: Sum of subarray minimums and subarray ranges

Prerequisites

Counting subarrays

Excluding endpoints of subarrays

Subarrays with non-unique minimums and maximums

LC 907. Sum of Subarray Minimums (approach 1)

LC 907. Sum of Subarray Minimums (approach 2, beast mode)

LC 2104. Sum of Subarray Ranges