Skip to main content

Working with binary trees on LeetCode using the binarytree package for Python

Daniel Farlow
Daniel Farlow
Software Engineer

This post describes how to effectively use the binarytree package for Python. Working with binary trees on LeetCode is a motivating use case for learning the package.

From the documentation home page:

Binarytree is Python library which lets you generate, visualize, inspect and manipulate binary trees. Skip the tedious work of setting up test data, and dive straight into practising algorithms. Heaps and binary search trees are also supported. Self-balancing search trees like red-black or AVL will be added in the future.

It notes Python 3.7+ as a requirement for use of the package. The source code for the package may be found either on the package's GitHub page or its own documentation site.

LeetCode​

Arguably one of the biggest selling points for the binarytree package is its ability to let you reproduce binary trees encountered when solving LeetCode problems. For example, consider LC 1026. Maximum Difference Between Node and Ancestor. We are told the definition for a binary tree node is as follows (this definition holds true for pretty much all LeetCode problems involving binary trees, except in some cases maybe val does not have a default value, left and right may not default to None, etc., but the structure is the same nonetheless):

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

The second example in the problem statement includes the following depiction of a binary tree:

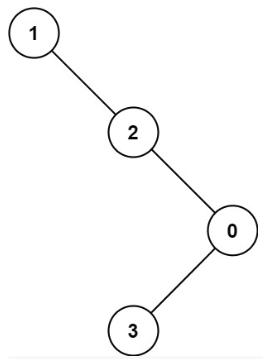
How could we reproduce this tree using our own code? We could create our own Node or TreeNode class and build it ourselves by establishing the root and then linking together all nodes, but this becomes quite cumbersome as the tree grows (imagine encountering a test case for a tree with over a thousand nodes). Fortunately, there's a much better alternative for building such trees, namely using the binarytree package.

The problem specifies as input the following for the tree above:

root = [1,null,2,null,0,3]

Can we somehow use this information to build the tree with the binarytree package? Yes! As the site documentation notes for the build2 function:

Binarytree supports another representation which is more compact but without the indexing properties (this method is often used in Leetcode).

Replace all instances of null with None for the root provided in the LeetCode input, and then use build2 to build the tree. We can then print the tree to see how it represents the image taken from LeetCode above:

Input
from binarytree import build2

lc_tree = [1,None,2,None,0,3]
print(build2(lc_tree))
Output
1
 \
  2__
     \
      0
     /
    3

A less compact way of building the tree above would be to use build, where we need to provide the list representation of the binary tree, where the list of node values is generated by index for a left-to-right breadth-first order starting from the root:

Input
from binarytree import build

lc_tree = [
  1,None,2,None,None,None,0,None,
  None,None,None,None,None,3
]
print(build(lc_tree))
Output
1
 \
  2__
     \
      0
     /
    3

The easiest way to tell the difference between build and build2 is how parent nodes play a role. For build2, starting with [1,None,2] indicates the left child of the root does not exist; thus, this cannot be the parent of any subsequent node. When we provide another value in our list, namely resulting in [1,None,2,None], this means None becomes the left child of 2 since 2 can actually be a parent. Providing 0 simply means 0 is now the right child of 2. Continuing on, the only legitimate parent now is 0, which means providing a value of 3 next results in 3 being the left child of 1. Hence, we only have to provide [1,None,2,None,0,3] to fully specify the tree.

The package documentation gives a more algebraic explanation for binarytree.build2:

List of node values like those for binarytree.build(), but with a slightly different representation which associates two adjacent child values with the first parent value that has not been associated yet. This representation does not provide the same indexing properties where if a node is at index i, its left child is always at 2i + 1, right child at 2i + 2, and parent at floor((i - 1) / 2), but it allows for more compact lists as it does not hold Nones between nodes in each level.

This is how LeetCode specifies its binary trees as input and allows for you to easily play around with possible tests cases.

Package API specification​

There's a lot more to the binarytree package. More details and examples may be added to this blog post in the near future. Regardless, the documentation site for the package outlines in detail its API specification: