Definitions

A

Algorithm

An algorithm is a procedure to accomplish a specific task, namely a well-specified problem, where the problem is specified by describing the complete set of instances it must work on and of its output after running on one of these instances. [20]

Understanding and Utilizing Algorithms Effectively

The distinction between a problem and an instance of a problem is critical. Determining that you are dealing with a general problem instead of an instance is your first step towards solving it. There are three desirable properties for a good algorithm. We seek algorithms that are correct, efficient, and easy to implement. Correctness may be formally verified by means of a proof (e.g., induction, contradiction, etc.) while efficiency is typically analyzed and established by means of Big-$O$ notation.

API wrapper

From Quora: An API-wrapper typically takes an API in one form and transforms it into another.

An example might be useful:

The main application interface to Flickr (the image hosting service) is a REST api (is http GET or POST calls). There is a library called pyFlickr which is a API-wrapper — it provides a Pythonic interface to Flickr — classes, methods, iterators using the REST API under the skin. It keeps all of the REST api methods intact and available, but you call them using Python function calls and wrappings.

Sometimes you will see the term binding, as in a Python binding for xyz; essentially this is different form of API-wrapper. Here the wrapper transforms an API designed for one programming language and provides functionality in a second language to call the original API. An example here is pyGTK. The original gtk api is written a a C library. pyGTK is called a Python binding for gtk as it allows a Python program to call the gtk API written in C.

Arithmetic sequence (math)

An arithmetic sequence is a sequence of the form

$$a, a+d, a+2d, a+3d, a+4d,\ldots$$

The number $a$ is the first term, and $d$ is the common difference of the sequence. The $n$th term of an arithmetic sequence is given by

$$a_n = a + (n-1)d$$

Arithmetic sequence partial sum

For the arithmetic sequence $a_n = a + (n-1)d$, the $n$th partial sum

$$S_n=a+(a+d)+(a+2d)+(a+3d)+\cdots+[a+(n-1)d]$$

is given by either of the following formulas:

1. $S_n = \frac{n}{2}[2a+(n-1)d]$
2. $S_n = n[(a+a_n)/2]$

B

Big Oh

Controlled chaos, abuse of notation, and the need for Ω and Θ

Controlled chaos: $O$ notation significantly simplifies calculations because it allows us to be sloppy — but in a satisfactorily controlled way. [8]

Abuse of notation: Donald Knuth notes in [8] that mathematicians customarily use the = sign as they use the word "is" in English: Aristotle is a man, but a man isn't necessarily Aristotle. Hence, in discussions of big oh, it is worth noting that the equality sign is not symmetric with respect to such notations; we have $n+1=O(n)$ and $n+2=O(n)$ but not $1=2$, nor can we say that $O(n)=n+2$.

Need for $\Omega$ and $\Theta$: As noted in [15], Big-$O$ notation is used extensively to describe the growth of functions, but it has limitations. In particular, when $f(x)$ is $O(g(x))$, we have an upper bound, in terms of $g(x)$, for the size of $f(x)$ for large values of $x$. However, big-$O$ notation does not provide a lower bound for the size of $f(x)$ for large $x$. For this, we use big-Omega notation. When we want to give both an upper and a lower bound on the size of the function $f(x)$, relative to a reference function $g(x)$, we use big-Theta notation. Both big-Omega and big-Theta notation were introduced by Donald Knuth in the 1970s. His motivation for introducing these notations was the common misuse of big-$O$ notation when both an upper and a lower bound on the size of a function are needed.

Functions assumed to be asymptotically nonnegative when working with O-Ω-Θ notation

The definition of $O(g(n))$ below requires that every function $f(n)$ in the set $O(g(n))$ be asymptotically nonnegative: $f(n)$ must be nonnegative whenever $n$ is sufficiently large. (An asymptotically positive function is one that is positive for all sufficiently large $n$.) Consequently, the function $g(n)$ itself must be asymptotically nonnegative, or else the set $O(g(n))$ is empty. We therefore assume that every function used within $O$-notation is asymptotically nonnegative. This assumption holds for the other asymptotic notations defined as well. [21]

The explanation above clarifies why other textbook authors (e.g., see [15]) sometimes write $|g(n)|$ instead of just $g(n)$.

The definitions that follow may be found in [21].

Worst case (big-O)

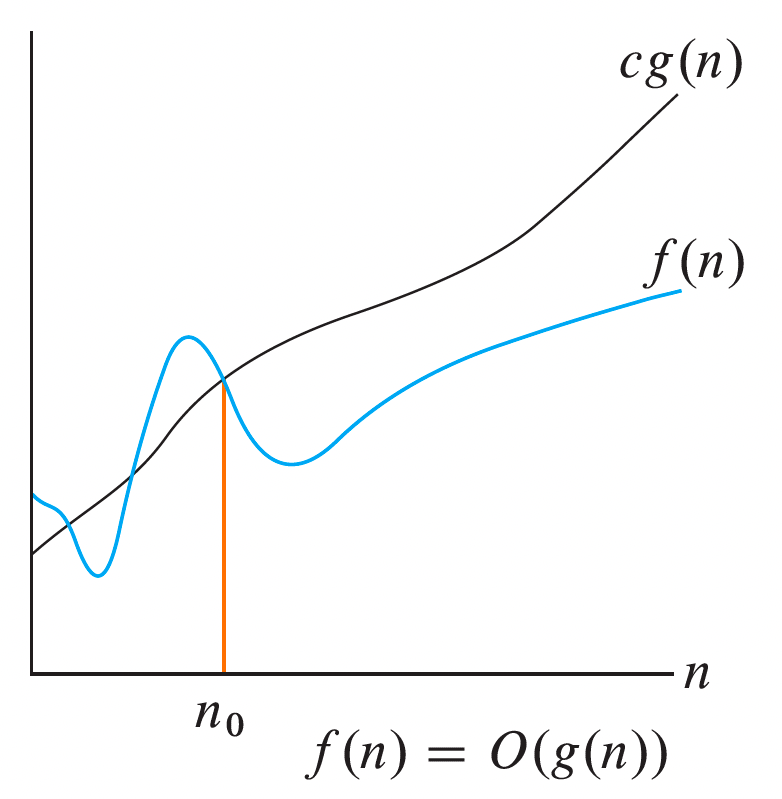
An asymptotic upper bound may be described with $O$-notation. Specifically, we use $O$-notation to give an upper bound on a function to within a constant factor.

For a given function $g(n)$, we denote by $O(g(n))$ the set of functions

$$\begin{align*} O(g(n)) = \{f(n) : {}& \text{there exist positive constants $c$ and $n_0$ such that}\\ & \text{$0\leq f(n)\leq cg(n)$ for all $n\geq n_0$} \} \end{align*}$$

A function $f(n)$ belongs to the set $O(g(n))$ if there exists a positive constant $c$ such that $f(n)\leq cg(n)$ for sufficiently large $n$. The following figure provides some intuition behind $O$-notation:

For all values $n$ at and to the right of $n_0$, the value of the function $f(n)$ is on or below $cg(n)$.

Big-O definition in terms of quantifiers

The definition above may be expressed more formally in the language of quantifiers as follows:

$$(\exists c, n_0\in\R^+)(\forall n\in\R)(n > n_0 \implies f(n)\leq cg(n))$$

Best case (big-Ω)

Just as $O$-notation provides an asymptotic upper bound on a function, $\Omega$-notation provides an asymptotic lower bound. For a given function $g(n)$, we denote by $\Omega(g(n))$ the set of functions

$$\begin{align*} \Omega(g(n)) = \{f(n) : {}& \text{there exist positive constants $c$ and $n_0$ such that}\\ & \text{$0\leq cg(n)\leq f(n)$ for all $n\geq n_0$} \} \end{align*}$$

The following figure provides some intuition behind $\Omega$-notation:

For all values $n$ at or to the right of $n_0$, the value of $f(n)$ is on or above $cg(n)$.

Big-Ω definition in terms of quantifiers

This definition may be expressed more formally in the language of quantifiers as follows:

$$(\exists c, n_0\in\R^+)(\forall n\in\R)(n > n_0 \implies f(n)\geq cg(n))$$

Average case (big-Θ)

We use $\Theta$-notation for asymptotically tight bounds. For a given function $g(n)$, we denote by $\Theta(g(n))$ the set of functions

$$\begin{align*} \Theta(g(n)) = \{f(n) : {}& \text{there exist positive constants $c_1$, $c_2$, and $n_0$ such that}\\ & \text{$0\leq c_1g(n)\leq f(n)\leq c_2g(n)$ for all $n\geq n_0$} \} \end{align*}$$

The following figure provides some intuition behind $\Theta$-notation:

For all values of $n$ at and to the right of $n_0$, the values of $f(n)$ lies at or above $c_1g(n)$ and at or below $c_2g(n)$. In other words, for all $n\geq n_0$, the function $f(n)$ is equal to $g(n)$ to within constant factors.

Big-Θ definition in terms of quantifiers

This definition, in light of the previous definitions for big-$O$ and big-$\Omega$, may be expressed more formally in the language of quantifiers as

$$(\exists c_1,c_2\in\R^+)(\exists n_1,n_2\in\R^+)(\forall n\in\R)(n > \max\{n_1,n_2\} \implies \underbrace{\overbrace{f(n)\leq c_1g(n)}^{f(n)=O(g(n))}\land \overbrace{f(n)\geq c_2g(n)}^{f(n)=\Omega(g(n))}}_{f(n)=\Theta(g(n))})$$

where the notation above is meant to reflect the fact that $f(n)$ is $\Theta(g(n))$ when $f(n)$ is $O(g(n))$ and $f(n)$ is $\Omega(g(n))$. With this in mind, we can let $n_0 = \max\{n_1,n_2\}$ and reframe the quantified definition more succinctly:

$$(\exists c_1,c_2,n_0\in\R^+)(\forall n\in\R)(n > n_0 \implies \underbrace{\overbrace{f(n)\leq c_1g(n)}^{f(n)=O(g(n))}\land \overbrace{f(n)\geq c_2g(n)}^{f(n)=\Omega(g(n))}}_{f(n)=\Theta(g(n))})$$

C

D

E

F

G

Geometric sequence (math)

A geometric sequence is a sequence of the form

$$a, ar, ar^2, ar^3, ar^4, \ldots$$

The number $a$ is the first term, and $r$ is the common ratio of the sequence. The $n$th term of a geometric sequence is given by

$$a_n=ar^{n-1}$$

Geometric sequence partial sum

For the geometric sequence $a_n=ar^{n-1}$, the $n$th partial sum

$$S_n=a+ar+ar^2+ar^3+ar^4+\cdots+ar^{n-1}\qquad(r\neq 1)$$

is given by

$$S_n=a\frac{1-r^n}{1-r}$$

Geometric series sum

If $|r|<1$, then the infinite geometric series

$$a+ar+ar^2+ar^3+ar^4+\cdots+ar^{n-1}+\cdots$$

has the sum

$$S=\frac{a}{1-r}$$

H

I

J

K

L

Logarithm results

• $y=\log_a x$ means $a^y=x$
• $\log_a a^x = x$
• $a^{\log_a x}=x$
• $\log_a 1=0$
• $\log_a a=1$
• $\log x=\log_{10}x$
• $\ln x=\log_e x$
• $\log_a xy=\log_a x+\log_a y$
• $\log_a\Bigl(\dfrac{x}{y}\Bigr)=\log_a x-\log_a y$
• $\log_a x^b = b\log_a x$
• $\log_b x=\dfrac{\log_a x}{\log_a b}$

M

N

O

P

Path (graph theory)

A path is a trail in which all vertices (and therefore also all edges) are distinct.

Q

R

S

Summation results

Powers of integers

• Sum of a unit $n$ times: $\displaystyle\sum_{k=1}^n 1=n$

• Sum of the first $n$ positive integers: $\displaystyle\sum_{k=1}^n k=\frac{n(n+1)}{2}$

• Sum of the squares of the first $n$ positive integers: $\displaystyle\sum_{k=1}^n k^2=\frac{n(n+1)(2n+1)}{6}$

• Sum of the cubes of the first $n$ positive integers: $\displaystyle\sum_{k=1}^n k^3=\frac{n^2(n+1)^2}{4}$

T

Time-sharing (computing)

Time-sharing is the ability for multiple users to share access to a single computer’s resources.

Historical Relevance

An Ars Technica article on the history of Linux also mentions time-sharing: "Thus [due to costs associated with operating and owning the GE 645], there was widespread interest in time sharing, which allowed multiple researchers to run programs on the mainframe at the same time, getting results immediately on their remote terminals. With time sharing, the programs weren’t printed off on punch cards, they were written and stored on the mainframe. In theory, researchers could write, edit, and run their programs on the fly and without leaving their offices. Multics was conceived with that goal in mind. It kicked off in 1964 and had an initial delivery deadline of 1967."

Trail (graph theory)

A trail is a walk in which all edges are distinct.

U

V

W

Walk (graph theory)

A walk is a finite or infinite sequence of edges which joins a sequence of vertices.

X

Y

Z