Topological order and topological sorting (with attitude)

This post explores what topological sorting is all about and includes two methods for obtaining a topological ordering on a DAG: Kahn's algorithm and a DFS-based approach. The DFS approach is then used in Kosaraju's algorithm to identify strongly connected components of a graph.

Attribution

The notes below come from the Algorithms with Attitude YouTube channel, specifically the Topological Order and Topological Sorting playlist comprised of the following videos: Introduction to Topological Sorting in Directed Acyclic Graphs, Kahn's Algorithm for Topological Sorting, Depth First Search Based Topological Sort, and Kosaraju's Algorithm for Strongly Connected Components.

There are several sections in this post, accessible in the table of contents on the right, but most of the sections have been listed below for ease of reference and navigation.

• Introduction to topological sorting in directed acyclic graphs (DAGs)
  • Partially ordered sets
  • Topological ordering for directed acyclic graphs
• Kahn's algorithm for topological sorting
  • Observation 1
  • Algorithm 1
  • Observation 2
  • Algorithm 2
  • Observation 3
  • Algorithm 3
  • Observation 4
  • Algorithm 4 (final algorithm)
  • Analysis
  • Summary of observations
  • Minor variations
  • Proof idea
  • Detailed example
  • Cycles?
• Depth-first search based topological sort
  • Concept - finding a last vertex
  • Stepping through depth-first search
  • Confirming our work
  • Algorithm
  • Why it works
  • Variants
• Kosaraju's algorithm for strongly connected components
  • Undirected graphs - components
  • Directed graphs - strongly connected components
  • Inefficient algorithm
  • Underlying component graph
  • DFS like undirected case
  • A better order
  • Clever observations
    • Clever observation 1
    • Clever observation 2
    • Clever observation 3
    • Clever observation 4
    • End result
    • Summary of clever observations
  • Efficient algorithm
  • Full example
  • Full example with code (Python)

Introduction to topological sorting in directed acyclic graphs (DAGs)

In this section, we'll cover the definitions we need for the remaining sections.

Partially ordered sets

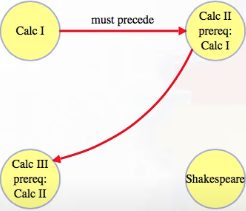
Usually when we think about sorting, we think about sorting things from a fully ordered set: for any two different numbers, one of them is smaller than the other (e.g., $12 < 34$), so to sort them we put the smaller one first. Other times, we might get some items that have to go in order, but only against some other items. For example, we probably want to take Calculus 1 before Calculus 2, $\text{Calculus 1} < \text{Calculus 2}$, but either one can come before or after a class on Shakespeare: $\text{Calculus 1}\;?\;\text{Shakespeare}$. A set like this is called a partially ordered set: it specifies an order between some pairs of items but doesn't need to fix an order between every pair.

For classes, to specify the important orderings, each course lists its prerequisites. If each class is represented by a vertex in a graph, then we can imagine those prerequisites as an incoming adjacency list for that class:

There are lots of different partially ordered sets. A standard example is the order you use to put on clothes. It doesn't matter if you put your left sock on before or after your right sock, but unless we're a superhero, we should put our underwear on before our pants.

Let's recap:

• Fully ordered sets
  • $12 < 34$
• Partially ordered sets
  • $\text{Calculus 1} < \text{Calculus 2}$
  • $\text{Calculus 1}\;?\;\text{Shakespeare}$
  • Calculus 2 prerequisite: Calculus 1
  • Pants prerequisite: underwear

Topological ordering for directed acyclic graphs

Topologically sorting a set just means putting its items into an order where, for every pair with a specified order, the one that needs to come before the other does:

It's also called a linear extension of a partial ordering. Modeling the partial ordering as a graph, with vertices for items, if we can arrange all of the vertices in a line so that all edges point to the right, then that line of vertices is a topological ordering for the items:

Note how the Shakespeare vertex could go anywhere. It doesn't depend on anything, and nothing depends on it. So it could go in any position in the ordering. The above is just one topological ordering (i.e., topological orderings are not necessarily unique):

• Calculus I
• Calculus II
• Shakespeare
• Calculus III

Also note that a topological ordering can be produced if and only if the graph is acyclic. In the context of the line of vertices and right-pointing edges, if we had a cycle, then at least some edge would have to point back to the left as a back edge.

Besides the explicit orders given, there can be implicit ones: if Calculus 1 is a prerequisite for Calculus 2, which is a prerequisite for Calculus 3, then Calculus 3 also has Calculus 1 as a prerequisite, even if it isn't directly listed.

The next two sections give linear-time algorithms to topologically sort items from a directed acyclic graph. We assume the graph is given in outgoing adjacency list format, arguably the most common representation form for graphs.

Kahn's algorithm for topological sorting

If we just want the clean, final, linear-time algorithm, then we can jump ahead to it, but we're going to approach this problem as if we're approaching it from scratch and go through the steps we might go through as if we had tried to come up with it ourselves.

Observation 1

To start, notice that if a vertex has no incoming edges, then it can go first. Also, in an acyclic graph, there has to be at least one vertex with no incoming edges: if we want to find one, start at an arbitrary vertex, and follow a path of incoming edges backwards. If we get to a vertex with no incoming edges, great. If not, then once we've gone back $|V|$ edges in a graph with $|V|$ vertices, then we must be repeating vertices, which means we have a cycle.

Let's recap:

• A vertex with no incoming edges can go first (this suggests the in-degree for graph nodes will play a part in developing an effective algorithm) — recall that a directed edge A -> B means B "depends" on A in the sense that A must come before B in whatever eventual topological ordering of the nodes we produce.
• A DAG must contain a vertex with no incoming edges or else we are dead in the water from the beginning (if no such node existed, then this would mean every node has a dependency and thus we do not have a sensible starting point); fortunately, by definition, a DAG has to have at least one node with no incoming edges (otherwise we would have a cycle).
• If we want to find a vertex with an in-degree of 0 (i.e., no incoming edges), then we can start at an arbitrary vertex and follow a path of incoming edges backwards:
  • If we get to a vertex with no incoming edges, then great!
  • If not, then once we've gone back $|V|$ edges in a graph with $|V|$ vertices, then we must be repeating vertices which means we must have a cycle.

Algorithm 1

The observations above make it possible for us to come up with a first, albeit inefficient, stab at an algorithm:

Algorithm 1

TopSort(G)
    while G isn't empty
        find u in V with no incoming edges
        put u next in the topological ordering
        remove u and all its outgoing edges from G

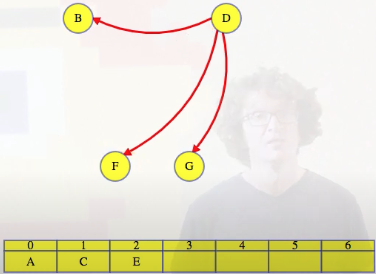
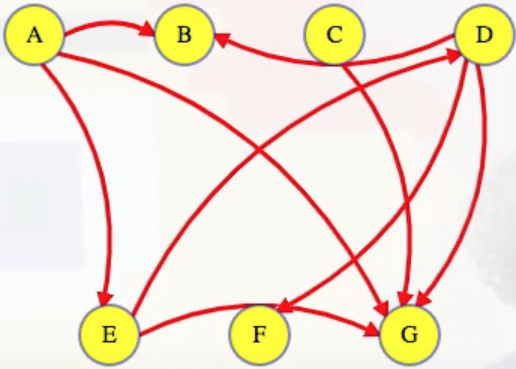
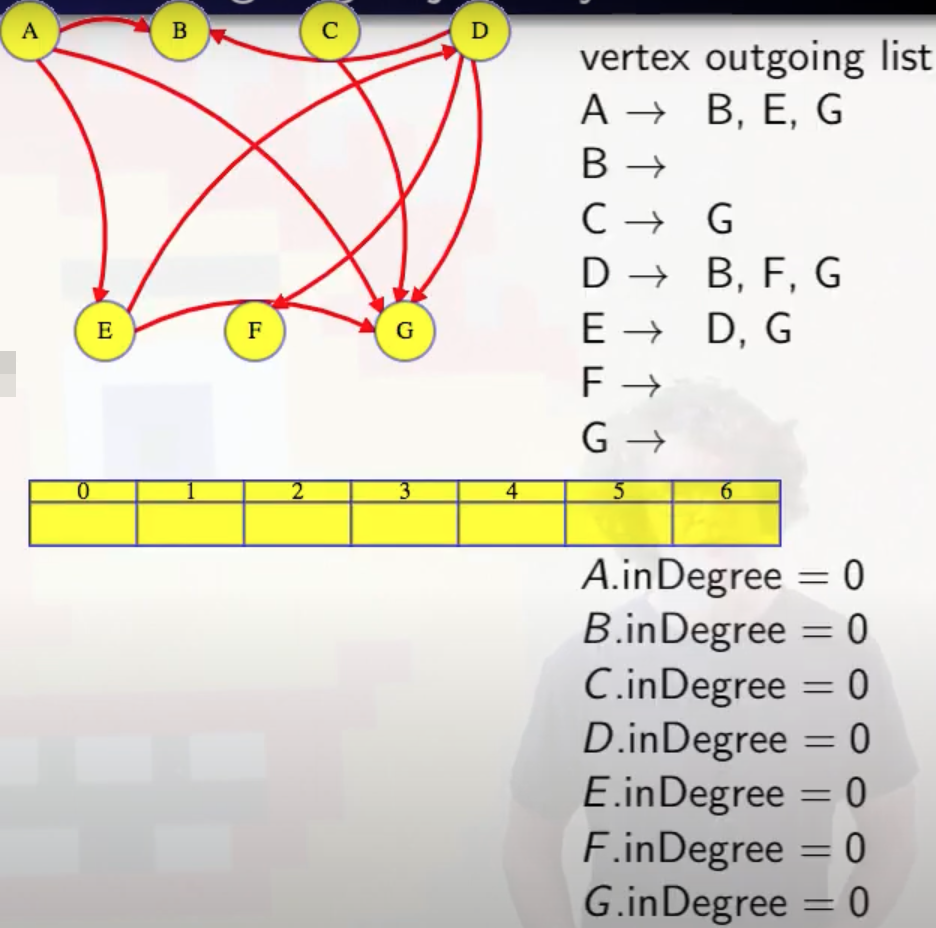
Find a vertex with no incoming edges to put first. In the graph below, this vertex could be A or C:

We'll use A because we'll break ties alphabetically. So this is how we would start (the single-row table added below and to the right will hold whatever topological ordering we end up finding):

Then remove that vertex and its outgoing edges from the graph:

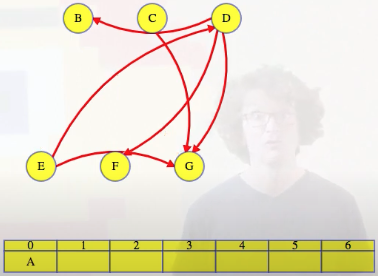
Then repeat for the remaining graph.

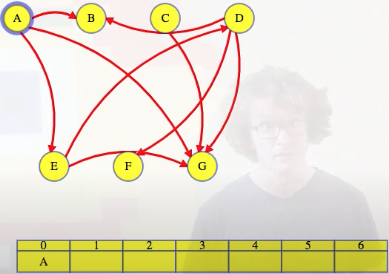
It's worth pausing for a moment and reflecting on why it makes sense to remove the outgoing edges from whatever vertex we identify as being next in the topological ordering. For example, above, we noted that A had no incoming edges, which means A does not have any dependencies. So we add it first to our topological ordering (C could have worked as well, but recall that we break ties alphabetically). Why does it make sense to then remove all outgoing edges from A, specifically A -> B, A -> G, and A -> E? Because removing these edges communicates to the other vertices that the A dependency has been resolved. For example, if we were to look at vertex E, then the edge A -> E communicates to E that the A dependency needs to be resolved before we can consider adding E to the topological ordering. If we delete the A -> E edge, then this effectively tells E that the A dependency has been resolved.

Returning to our example, if we look at the graph above, where A has been removed along with its outgoing edges, then we see that C or E could go next. We'll pick C since we're using an alphabetical tie-breaker:

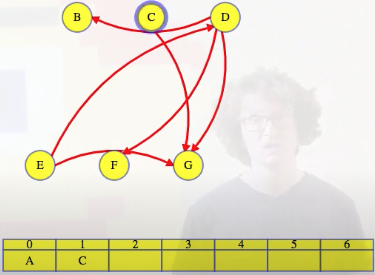
We delete C's outgoing edge:

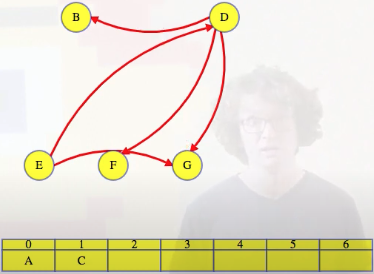
And then move to E:

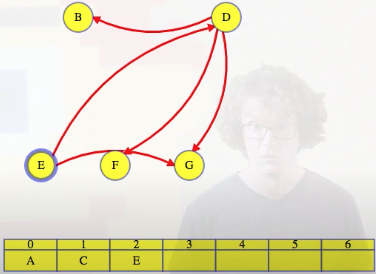
Delete E's outgoing edges:

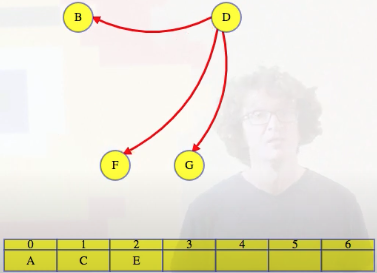
And then we just continue on like this until all vertices are ordered:

Vertex E and outgoing edges just removed

1 / 9

The algorithm above works. Its efficiency depends on implementation details, but if we get the graph in outgoing adjacency list format, then finding a vertex with no incoming edges might take a while (line 3 in the pseudocode), and we do that once for each vertex we put into the ordering.

Observation 2

To make our algorithm faster, maybe we don't need to do that (i.e., find a vertex with no incoming edges) from scratch after every vertex. To start the algorithm, in time linear for the size of the graph, we can create an incoming adjacency list for each vertex. With those incoming adjacency lists, we can find all vertices with no incoming edges, and those are the vertices that can go first. We can add all of those vertices to make an ordered list of vertices that are ready to go, A and C below:

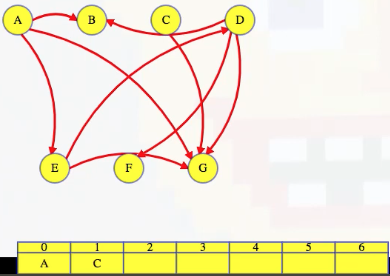
Vertex A goes first:

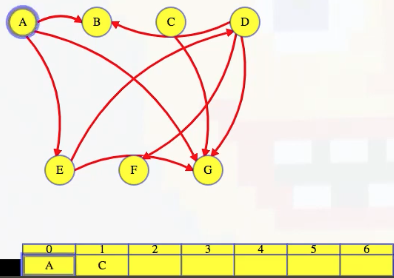
We use vertex A's outgoing adjacency list to figure out which edges to delete from the incoming adjacency lists of B, then E, then G. When we delete A's edge to vertex E, we see it is E's last incoming edge, so we can add E to the end of our growing ordered list. Finally, we delete A from G's list, and then we finish deleting A from the graph:

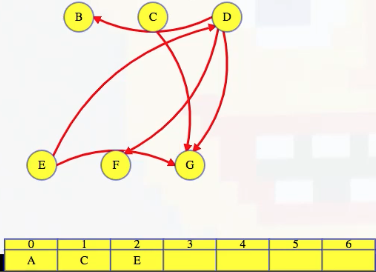
Here's what the whole process looks like using this approach, picking up from right before we delete A:

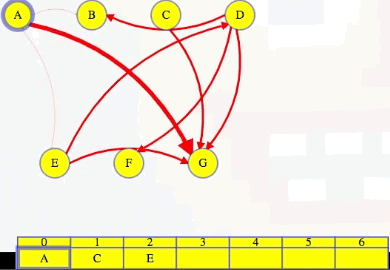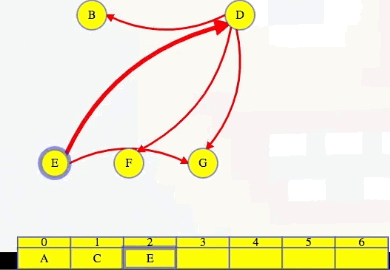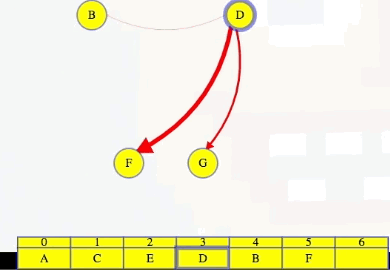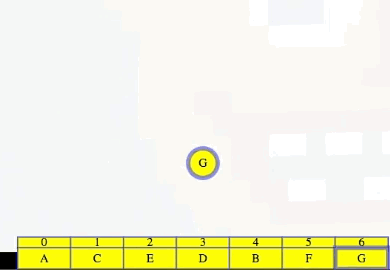
As shown in the animation above, we repeat the same steps for each vertex, where each time we get to a vertex, we look at its outgoing edges, delete them from the corresponding incoming adjacency lists, and if it's the last incoming edge for a vertex, then we add that vertex to our list.

Let's summarize this second set of observations we've been discussing:

• There's no need to start from scratch each time:
  • Compute incoming adjacency list just once to start
  • Grab a set of all 0 in-degree vertices
  • Find new 0 in-degree vertices as vertices are removed from the graph

Algorithm 2

If we incorporate the new observations into pseudocode for an improved algorithm, then we will have something like the following:

Algorithm 2

TopSort(G)
    create incoming edge adjacency list for each vertex (time linear in the graph size)
    S = ordered list
    add all vertices with no incoming edges to S (order V time)
    while not done with S
        consider next vertex u from S
        put u next in the topological ordering
        while removing u and its outgoing edges from G
            if vertex v's incoming edge list becomes empty
                add v to S

• First, calculate incoming adjacency lists (line 2), which takes time linear in the size of the graph
• Then add a list of all finished vertices (i.e., vertices with no incoming edges) in order $O(|V|)$ time (line 4)
• Finally, for each vertex in our list that we consider, use its outgoing edges to modify those newly created incoming adjacency lists (lines 8-10).

Now we don't have to scan the whole graph to look for new vertices to go next. This algorithm still follows the idea of the first one, but it's a bit more efficient in its implementation because it decreases some of the repeated work.

Observation 3

We can now do a little bit of clean up. Because of some of the changes we just made to the algorithm, we don't need to delete the vertex u from the graph anymore. We just need to delete it from the incoming adjacency lists it is in.

We can imagine using those lists that we created at the start of the algorithm (i.e., the incoming adjacency lists) as working space while the outgoing lists don't have to change at all (i.e., we don't actually modify the graph representation).

Also, that first round of changes introduced a bit of clutter. We don't need to have one ordered list of vertices that are ready to go (i.e., S) and another for our topological order (i.e., the implied topological ordering list referred to by the line put u next in the topological ordering), especially since both of them are in the same order. We can drop the extra list (i.e., the topological ordering list).

The details behind not needing to keep two different orders sets with the same order

Recall Algorithm 2:

TopSort(G)
    create incoming edge adjacency list for each vertex (time linear in the graph size)
    S = ordered list
    add all vertices with no incoming edges to S (order V time)
    while not done with S
        consider next vertex u from S
        put u next in the topological ordering
        while removing u and its outgoing edges from G
            if vertex v's incoming edge list becomes empty
                add v to S

There are two separate lists being maintained:

1. S: This is our working list, often implemented as a queue or stack, that contains vertices with no incoming edges. It's the set of vertices that are ready to be processed next.
2. topological ordering list (implied): This is a separate list where we explicitly place each vertex u as we process it, building up the final topological order.

Here's how the two lists function in the context of the algorithm above:

• S (working list of ready vertices):
  • Initialized with all vertices that have no incoming edges.
  • Used to keep track of which vertices are ready to be processed.
  • Vertices are added to S when they have no remaining incoming edges (i.e., when all their predecessors have been processed).
• topological ordering list:
  • Starts empty and is built up as the algorithm proceeds.
  • Each time a vertex u is taken from S, it is placed into this list using the line put u next in the topological ordering.
  • Represents the final result: the topological order of the vertices.

We can actually remove the line put u next in the topological ordering because we realize that the order in which we process the vertices from S inherently gives us the topological order. Since vertices are only added to S when all their incoming edges have been removed (i.e., all their prerequisites have been processed), the sequence in which we remove vertices from S is already in topological order.

Thus, we can eliminate the separate topological ordering list and simply output the vertices in the order they are processed from S. This streamlines the algorithm by reducing it to a single list, S, that serves as both the working list and the implicit topological ordering.

In summary, the second algorithm works with two lists:

• S: The worklist of vertices ready to be processed (no incoming edges).
• topological ordering list: A separate list where vertices are placed in topological order as they are processed.

By recognizing that these two lists can be combined (since the order of processing from S gives the topological order), we can simplify the algorithm by maintaining only S.

These observations can be summarized as follows:

• Remove vertices from incoming adjacency lists, not from the graph as a whole
• No need to keep two different ordered sets with the same order

Algorithm 3

The following algorithm reflects our clean up observations above:

Algorithm 3

TopSort(G)
    create incoming edge adjacency list for each vertex (time linear in the graph size)
    S = ordered list
    add all vertices with no incoming edges to S (order V time)
    while not done with S
        consider next vertex u from S
        for each outgoing edge u -> v
            remove u from v's incoming list
            if v's incoming list is empty
                add v to S

How efficient is the algorithm now?

The initialization stuff takes linear time, and assuming that we can add to and get the next vertex from S in constant time (e.g., either using a queue or stack), going through all vertices and edges takes linear total time, excluding the time to remove edges from the incoming lists (line 8). But that removal, for each edge, take some non-constant time. It might be a bit slow.

Linked lists or array lists can take linear time in the in-degree, and a balanced tree would take logarithmic time. Without analyzing it exactly, can we do better?

Observation 4

How do we actually use the incoming adjacency lists? The last few lines of our algorithm above tells us:

# ...
for each outgoing edge u -> v
    remove u from v's incoming list
    if v's incoming list is empty
        add v to S

The only thing we use each one for is to see if it is empty (highlighted line above). We're just keeping these perfect lists, and deleting exactly the right edge from each in order to see if it's empty. We never actually use the list contents, only its size. So just track the size! Instead of incoming adjacency lists, track in-degrees, and decrement them instead of deleting edges. If they go to 0, then add them to the list. That's the whole algorithm.

Algorithm 4 (final algorithm)

Algorithm 4

TopSort(G)
    find inDegree for each vertex
    S = ordered list
    add all vertices with no incoming edges to S
    while not done with S
        consider next vertex u from S
        for each outgoing edge u -> v
            decrement v's inDegree
            if v's inDegree is 0
                add v to S

Analysis

Finding all in-degrees takes linear time. Over the course of the entire algorithm, each vertex is added to the list at most once, either at the start if it has no incoming edges, or when its in-degree gets decremented to 0. Each vertex in the list is considered at most once, and each edge from the vertex causes at most one constant time decrement.

So the algorithm takes time linear in the graph size.

Summary of observations

Before considering some minor variations, let's concisely summarize the four observations we considered that led to our final algorithm:

1. A vertex with no incoming edges can go first.
   • DAGs must contain a vertex with no incoming edges.
2. No need to start from scratch each time:
   • Compute incoming adjacency list just once to start.
   • Grab a set of all 0 in-degree vertices.
   • Find new 0 in-degree vertices as vertices are removed from the graph.
3. Clean up:
   • Remove vertices from incoming adjacency lists, not from the graph as a whole.
   • No need to keep two different ordered sets with the same order.
4. We don't care what the incoming edges are, only the in-degree.

Minor variations

Something to note when developing this algorithm: what if we had made the last changes to deal with in-degrees instead of incoming lists but kept the separate topological order, alongside the ordered list:

TopSort(G)
    find inDegree for each vertex
    S = ordered list
    add all vertices with no incoming edges to S
    while not done with S
        consider next vertex u from S
        put u next in the topological ordering
        for each outgoing edge u -> v
            decrement v's inDegree
            if v's inDegree is 0
                add v to S

The algorithm still runs in linear time. What if we replaced our ordered list, S, with a queue:

TopSort(G)
    find inDegree for each vertex
    S = FIFO queue
    add all vertices with no incoming edges to S
    while not done with S
        consider next vertex u from S
        put u next in the topological ordering
        for each outgoing edge u -> v
            decrement v's inDegree
            if v's inDegree is 0
                add v to S

Or even a stack:

TopSort(G)
    find inDegree for each vertex
    S = LIFO stack
    add all vertices with no incoming edges to S
    while not done with S
        consider next vertex u from S
        put u next in the topological ordering
        for each outgoing edge u -> v
            decrement v's inDegree
            if v's inDegree is 0
                add v to S

It still works. And still in linear time. The stack-based version above uses the order that things are removed from the stack, but what if we used the order that things went in to the stack:

TopSort(G)
    find inDegree for each vertex
    S = LIFO stack
    add all vertices with no incoming edges to S and ordering
    while not done with S
        consider next vertex u from S
        for each outgoing edge u -> v
            decrement v's inDegree
            if v's inDegree is 0
                add v to S
                put u next in the topological ordering

It still works. And still in linear time.

This is a problem where, after a few iterations, we can have a lot of different versions, all asymptotically efficient. The ordered list we use for S is very flexible (e.g., queue, stack, linked list, array, etc.).

Proof idea

TopSort(G)
    find inDegree for each vertex
    S = ordered list
    add all vertices with no incoming edges to S
    while not done with S
        consider next vertex u from S
        for each outgoing edge u -> v
            decrement v's inDegree
            if v's inDegree is 0
                add v to S

Lines like "not done with S" are pretty informal. We may want more precise pseudocode if we want to try to formally prove that the algorithm works. But all of the variants discussed in the previous section will have similar proofs.

We could use a loop invariant, stating that no vertex gets added to the list until all vertices that must precede it have been considered as vertex u. For each vertex, the in-degree represents the number of vertices with edges to that vertex that have not yet been considered as vertex u:

TopSort(G)
    find inDegree for each vertex
    S = ordered list
    add all vertices with no incoming edges to S
    while not done with S               # nothing added to S until after vertices
        consider next vertex u from S   # with edges to it are considered in S
        for each outgoing edge u -> v
            decrement v's inDegree
            if v's inDegree is 0        # inDegree = number of incoming edges not yet considered for v
                add v to S

The invariant initially holds when vertices with no incoming edges are added to the list, because no vertices need to precede them. It gets updated each time a new vertex u is used to decrement in-degrees, which is the only way those values get decreased.

Detailed example

Using the algorithm above, we can work through the following example, vertex by vertex, decrement by decrement:

Detailed example illustration (beginning to end)

Cycles?

What happens if there is a loop in the graph? The algorithm above won't find a topological order because one doesn't exist for a graph with cycles. But what happens if we run the algorithm on a graph with a loop anyway?

Any vertex on a cycle will never get down to in-degree 0, so it will never be added to the list. The list returned by the algorithm will only include vertices that aren't in, or reachable from, any cycle. We can just check the size of the list to see if we have the whole graph or not. If not, then what we choose to do depends on why we were finding the topological order in the first place.

In summary:

• The algorithm won't ever decrement the in-degree of any vertex on a cycle to 0.
• Vertices reachable from cycles won't ever get to in-degree 0 either.
• The final list won't include these vertices. Check its size.

Depth-first search based topological sort

For the sections that follow, we assume the graph is given to us in outgoing adjacency list format.

Concept - finding a last vertex

The idea behind Kahn's algorithm was to find a vertex that can go first, and then work from the beginning. Of course, we could also try to find something that goes last and work our way backwards towards the first item.

To do that, we could modify Kahn's algorithm to work from the back (i.e., build incoming lists and then use out-degrees to run Kahn's algorithm from the end), but then that would just be Kahn's algorithm in a different guise. It might be slightly slower than before, because it first converts the graph into the incoming edge adjacency list representation. That incoming vs. outgoing adjacency list is the only non-symmetrical difference between finding the ordering front to back or back to front.

Another way to find a vertex that can go last is to just run depth-first search (DFS) on the outgoing lists until we get to a vertex with no outgoing edges. That vertex can go last.

Stepping through depth-first search

The graph below is the same example graph we used when exploring Kahn's algorithm, with room at the bottom for an ordering:

But we'll rearrange it to make the depth-first search tree easier to see:

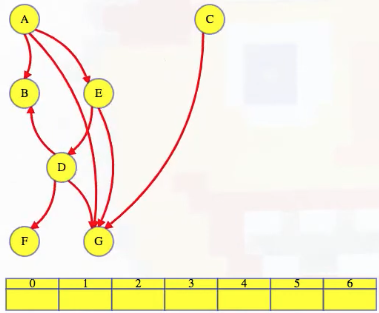
If we run depth-first search alphabetically, then we start at vertex A, and then we find vertex B along a tree edge (we'll color tree edges with heavy red). Since B has no outgoing edges, it can go last in our topological order:

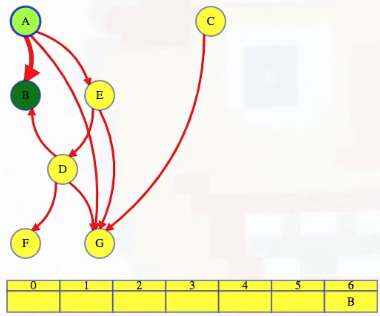
Our depth-first search finishes B and returns to A, which has two other outgoing edges. If we want to, we can continue our depth-first search, looking for other vertices that have no outgoing edges. But let's stop for just a second and think about what the edges from vertex A mean.

In the graph above, A has edges to B, E, and G, so A has to go before each of those vertices in the topological order. Even more than that, A has to go before any vertex that it can reach in the entire graph, either because it has a direct edge to them or because it has a longer path to them (e.g., vertex D). If A has to precede E, and E has to precede D, then A has to precede D. But what vertices are reachable from A? Exactly those that we will reach when we run depth-first search on A. Vertex A can go in the topological order as long as it is before everything that is discovered in the course of a depth-first search on it.

If we continue the search, then we go to E, then D, and we see a cross edge to B. So we go back to D and then to F, which has no outgoing edges so then F can go last (i.e., out of the remaining vertices):

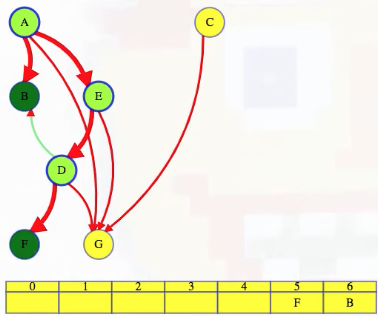
When depth first search returns to D, just like with vertex A, vertex D has to precede everything that it can reach in its depth-first search.

Continuing that search of D, we get to G, see that it has no outgoing edges, and then we put it after all remaining vertices (i.e., vertices waiting to be finished):

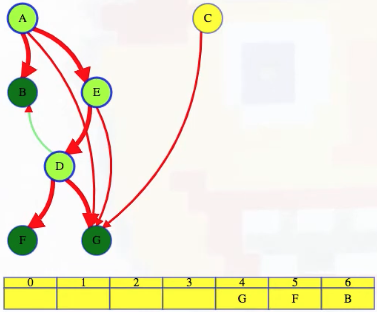
Now, when we return to D, all of its outgoing edges have been explored. Everything that has to follow it in the topological ordering, everything it can reach, F and G above, have already secured a slot in the ordering after D. So D can go last out of all the unfinished vertices:

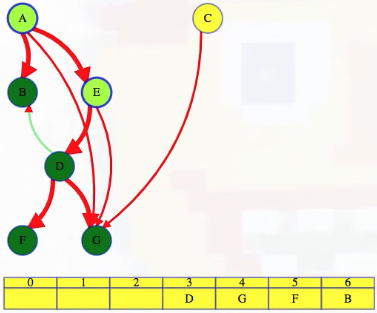
We continue our depth-first search. E has a forward edge and then finishes so we can put it in the latest unreserved slot:

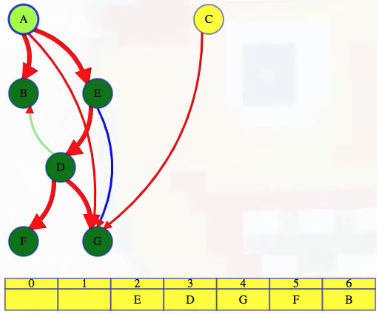
Vertex A has a forward edge to G and then finishes so we can put it in the latest open slot:

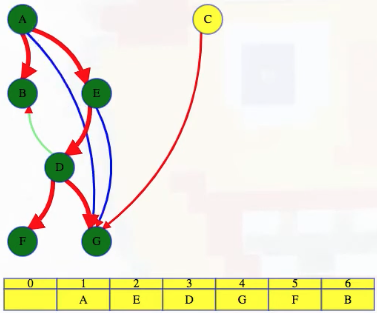
Whenever we finish a vertex, we put in the latest remaining unreserved slot in our topological order. We continue the search on the entire graph, not just the top-level call on vertex A. The top-level search ignores B because it's already searched, but C isn't. But when C finishes, it will add C to the front of the order. Everything else is already explored so all other top-level searches will just move on (i.e., when executing DFS on all nodes of the graph, starting from A gives us everything except C; once C is done, all other vertices will be skipped):

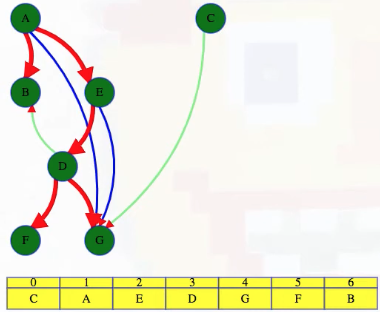
We can now admire our work:

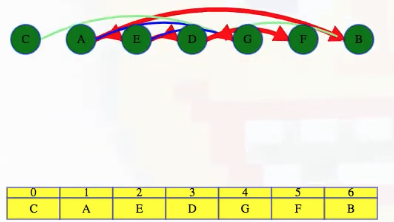
Rearranging the graph into the order above, we can see that all edges go from left to right. So the algorithm worked even though it happens to give a different order than the one we got from Kahn's algorithm.

Let's summarize the core parts:

• Vertices with no outgoing edges can go last
• Vertices must go before everything they can reach
• Once everything reachable by a vertex has reserved later times, a vertex can go after the unscheduled remaining vertices.

Confirming our work

We can use previous work to investigate the DFS output more thoroughly, specifically the discovery and finish times for different vertices as well as all edge classifications:

Loading...

Output

Click "Run Code" to see the output here

The output from running the code above, which can be directly verified, is the following (reformatted for the sake of clarity):

""" 

(   A  B   C   D   E  F  G
  [ 1, 2, 13,  5,  4, 6, 8],    # discovered
  [12, 3, 14, 10, 11, 7, 9],    # finished
  [-1, 0, -1,  4,  0, 3, 3],    # predecessors
  {                             # edge classifications
    ('A', 'B'): 'treeEdge',
    ('A', 'E'): 'treeEdge',
    ('E', 'D'): 'treeEdge',
    ('D', 'B'): 'crossEdge',
    ('D', 'F'): 'treeEdge',
    ('D', 'G'): 'treeEdge',
    ('E', 'G'): 'forwardEdge',
    ('A', 'G'): 'forwardEdge',
    ('C', 'G'): 'crossEdge'
  }
)

"""

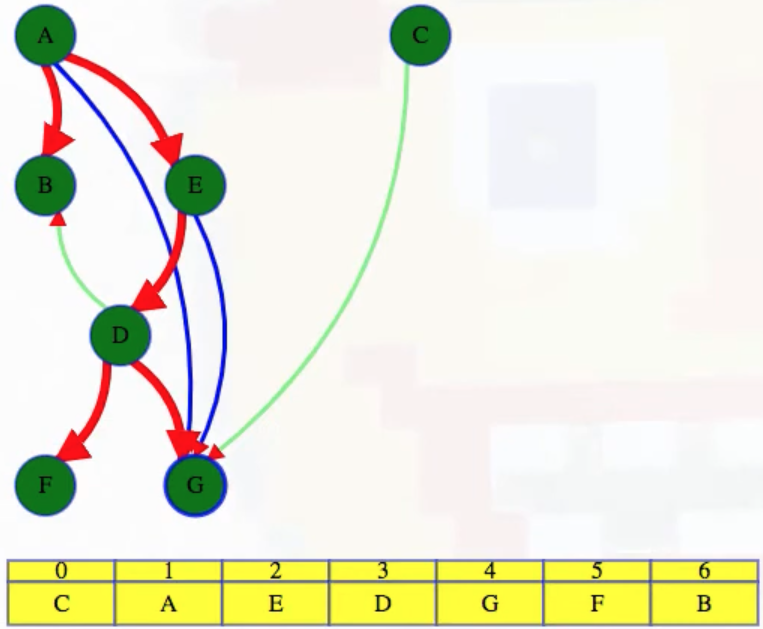
It's worth noting that the topological sort perfectly aligns with the reverse order in which vertices were finished in the DFS:

# Topological order: C A E D G F B

# finish times
#   A  B   C   D   E  F  G    <- node correspondence
# [12, 3, 14, 10, 11, 7, 9]   <- unordered finish times
# ...
# [14, 12, 11, 10, 9, 7, 3]   <- reverse order of finish times
#   C   A   E   D  G  F  B    <- topological order

We can also confirm all of the edge classifications as they appear in the video (red edges are tree edges, blue edges are forward edges, and green edges are cross edges):

Algorithm

Just to clarify, what was the actual algorithm we used when stepping through the example in the section before last? It's super simple: run depth-first search on the entire graph, and set our topological order to be the reverse order of the vertex finish times. That's it:

• Run depth-first search on entire graph
• Set the topological order to be the reverse order of vertex finish times

That's it. Because the graph is acyclic, when depth-first search on a vertex completes, everything that vertex can reach has been explored — as long as the vertex is before those things in the ordering, it's set.

To topologically sort, we don't really need the start or finish times. We could modify depth-first search to return the topological ordering directly (or run DFS and then counting sort on finish times).

Why it works

The following graphic does a decent job of giving some intuition as to why this DFS algorithm works for producing a topological ordering when the graph is acyclic:

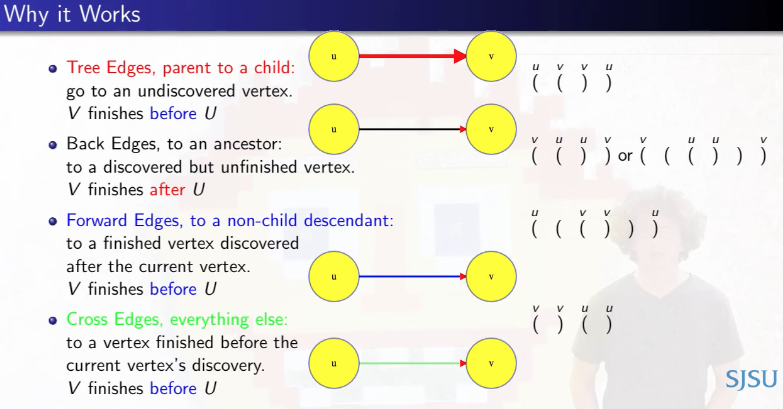
Specifically, using parthensis notation and edge classifications (both remarked on in another post about DFS), note that for tree edges, forward edges, and cross edges, the closing parentheses for v come before the closing parentheses for u, which is what we want for all edges u -> v since u -> v implies that v has u as a dependency that needs to be resolved and thus u must come earlier in the ordering. For the three edge classifications above, v will finish before u. So if we take vertices in reverse order of finish time, then any edge from u to v will put v after u, just like we need it to be.

The only problem is back edges, where vertex u would finish before v. But for depth-first search on an acyclic graph, there are no back edges since a back edge completes a cycle between a vertex and its ancestor. So don't worry about back edges (unless we're not guaranteed the input graph is acyclic, in which case we need to implement logic for cycle detection).

Variants

Two things worth considering in regards to possible variations of the implementation we've been discussing:

1. Subset of vertices: If we only want to consider vertices reachable from a subset of vertices, maybe even a single vertex, then simply modify the top-level depth first search to only search from that subset or that one vertex. The recursive part doesn't change.
2. Non-recursive DFS: If we're possibly at risk of a stack overflow, then it may be beneficial to consider an iterative implementation of DFS instead of the recursive implementation.

Finally, it's important to note that if we run our recursive DFS algorithm for finding a topological ordering on a graph that does have cycles, then unlike Kahn's algorithm, our algorithm will return an order including all vertices. Of course, the order returned isn't a topological order (because that doesn't exist for a graph that has cycles), but it can still be helpful due to some special properties that can be exploited based on finishing times. Kosaraju's algorithm for finding strongly connected components (SCCs) makes use of such a non-topological order.

Kosaraju's algorithm for strongly connected components

Undirected graphs - components

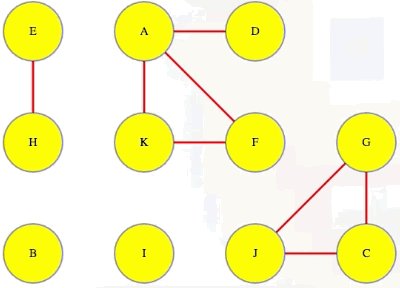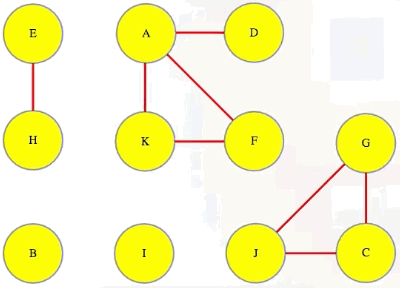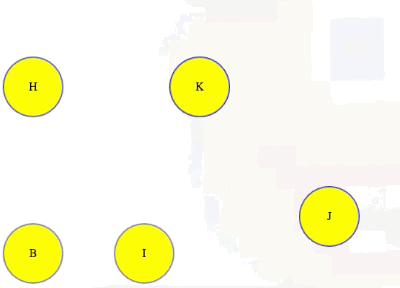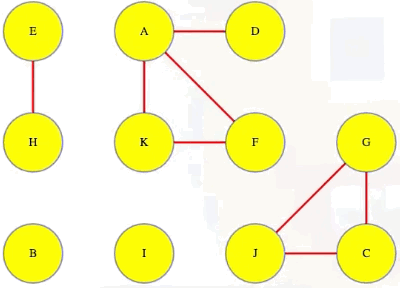
Kosaraju's algorithm is all about finding strongly connected components, but this does us little good if we do not even know what a component is. In an undirected graph, components are the different connected pieces of the graph:

If there's any path from one vertex to another, then these vertices are in the same component:

If the entire graph is connected, then it has just one component.

One easy way to partition the graph into its separate components is to run depth-first search on the entire graph, and each time that a top-level call finds a previously undiscovered vertex, then that vertex's depth-first search will discover its entire component:

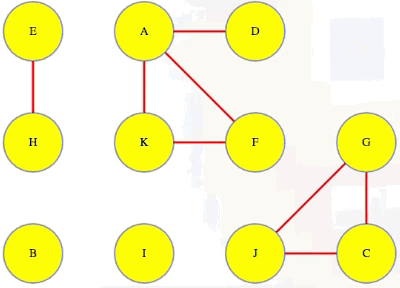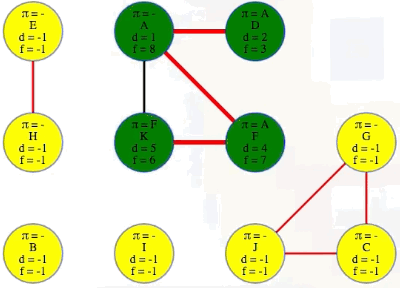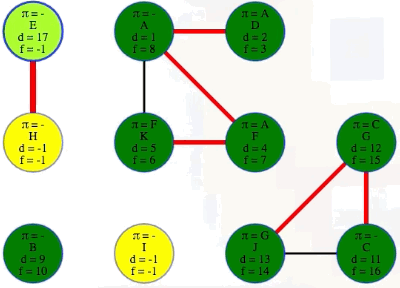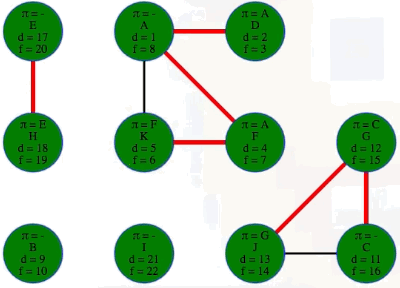
Above, we can see that A discovers D and F directly and then discovers K indirectly (through F), and that is the first component found. Top-level searches for B and C discover their components, but D is already discovered so its top-level search will just exit right away so that we can move on to E (i.e., in the context of executing DFS on an entire graph, we execute top-level searches on each vertex, A through J, in alphabetical order for ease of reference):

When all top-level DFS calls finish, we have some tree and back edges (colored red and black, respectively):

And each of the trees in the depth-first search forest makes one component:

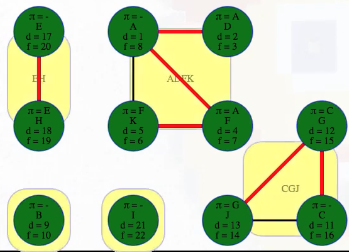
Let's recap what we've discussed for undirected graphs:

• Items connected by a path are in the same component.
• If the graph is connected, then all vertices are in one component.
• Find components using depth-first search on the graph:
  • Top-level search on previously undiscovered vertex: new component.
  • Vertices discovered during top-level search: that vertex's component.

Directed graphs - strongly connected components

Now suppose our graph is directed:

Then how do we actually define what a "component" is?

Above, if A has a path to G but G has no path back to A, then are A and G in the same component? We say that two vertices are strongly connected if each has a path to the other (i.e., they lie on some cycle with each other). Vertices in a directed graph are partitioned into strongly connected components — each component is a subset of vertices that can all reach each other. Each vertex will be in exactly one component along with the vertices that it can reach and that can reach it:

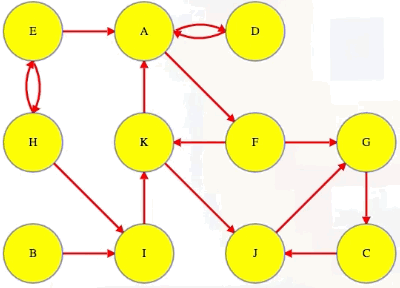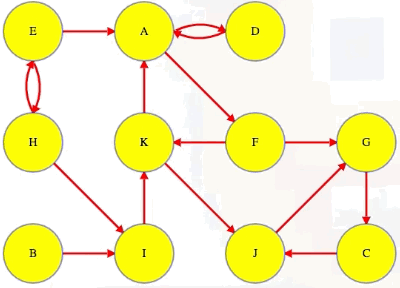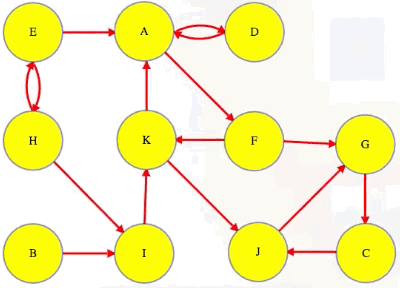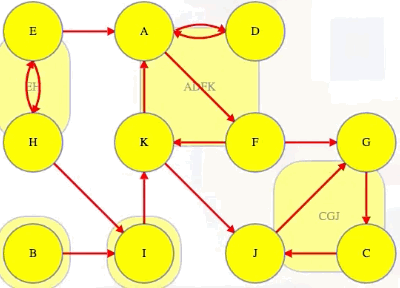
Notice that A and D are in the same component and so are A and F:

Because of this, D and F have to be in the same component: they can each reach each other through their paths to and from A. If a vertex isn't in any cycle, then even if it has edges in and out of it, it's all alone in its own component (e.g., vertex I).

Let's recap what we've discussed for directed graphs: two vertices are strongly connected if each has a path to the other.

• Some cycle exists with both vertices.
• The graph is partitioned into strongly connected components: a set of vertices which can all reach each other.
• If A and D can reach each other, and A and F can reach each other, then D and F can reach each other.

Inefficient algorithm

Our goal is to find strongly connected components from a graph, ideally with an efficient algorithm. If we don't care about efficiency, then we can come up with an algorithm with relative ease: grab a vertex like A, see what it can reach, maybe with DFS:

Then, if we reverse the graph (i.e., swap the direction of all edges to create the transpose of the graph) and search the same vertex A again, then we can see what can reach vertex A in the original graph:

By superimposing one result onto the other, we can see the intersection of those two sets, the vertices that can both be reached from A (first DFS) as well as can be used to get to A (second DFS on reversed graph):

Here's the entire process in one go for vertex A:

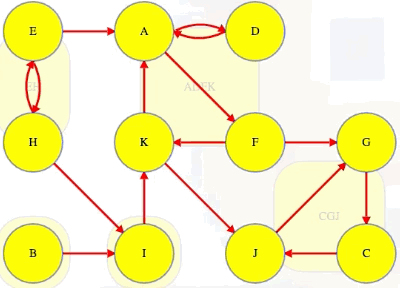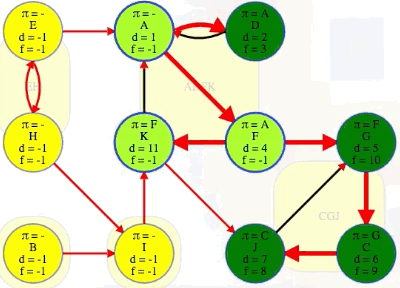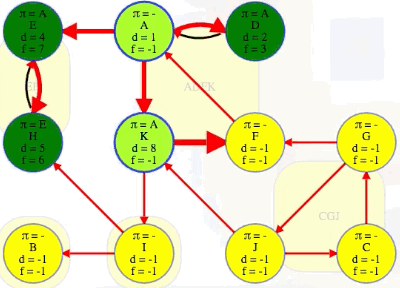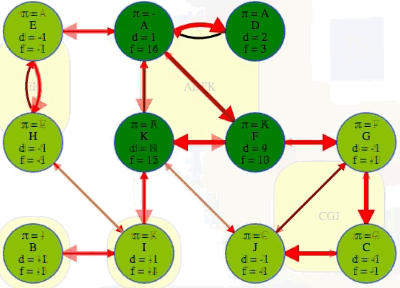
The process above conclusively tells us what strongly connected component A belongs to:

We could do the same search for every vertex in the graph, but we only need to do it once per component. For example, once we know D is in A's component, we don't need to repeat that work on D.

To summarize, the following would be an inefficient but doable algorithm:

1. Search from a vertex to see what it can reach.
2. Search from the same vertex in the reverse graph to see what can reach it.
3. Intersect those two sets to find its strongly connected component.
4. Repeat with other vertices.

How long this algorithm takes depends on how we implement it, but it would be pretty easy to find one component in time proportional to the size of the graph. Hence, if there are $X$ strongly connected components, then we would be looking at $O(|V| + |E|)$ time per component, which would give us a total time complexity of $O(X(|V| + |E|))$.

Underlying component graph

If we want better efficiency, then let's stop to really think about the strongly connected components. Let's collapse vertices from each component into one "super-vertex" and draw edges between super vertices if there are any edges between their corresponding sets of vertices:

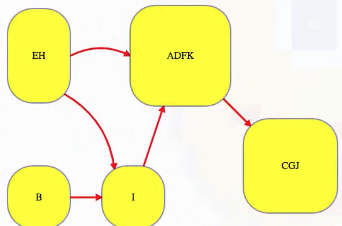
This new graph, the underlying component graph (i.e., the graph above), must be acyclic. Why? Because if it had a cycle, then all vertices from the cycle's corresponding vertices in the original graph could all reach each other through some combination of intra and inter-component edges — all such connected vertices could be collapsed into one component. If the original graph is acyclic, then the underlying component graph looks just like the original graph — every vertex would be its own component.

Both topological order algorithms discussed previously (i.e., Kahn's algorithm and the DFS-based algorithm) each found topological orders either from the beginning (Kahn) or the end (DFS) of the ordering. Our hope: maybe it's easier to find strongly connected components if we do it by topological order for the underlying component graph:

Let's recap what we've discussed concerning the underlying component graph:

• Collapse vertices from each component into one super-vertex.
• Add edges between components if there is an edge between corresponding sets in the original graph.
• The underlying component graph is acyclic.
• Both of our topological sorts (Kahn and DFS) found orders from the beginning or end.
• Our hope: strongly connected components are easier to find in topological order.

DFS like undirected case

We started our discussion of Kosaraju's algorithm by finding components in an undirected graph with DFS. In that context, with an undirected graph, we didn't need to intersect the set of vertices from the first search with the vertices from the second search.

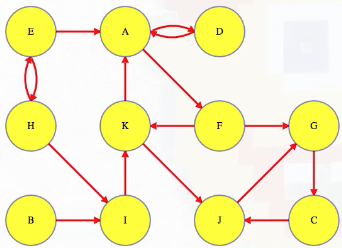
Let's now consider the following directed graph:

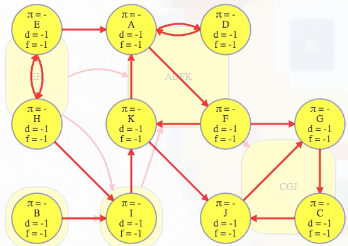
Imagine if we could (magically) start a search on a vertex in the topologically last component, maybe C in the graph above. We would discover C's strongly connected component in time linear to the number of vertices and edges in that component. We wouldn't need to reverse the graph and do another search and find the intersection. We would just discover the component and be done with it because C's component is topologically last, which means the search can't escape it (i.e., its strongly connected component has no outgoing edges, as illustrated in the underlying component graph):

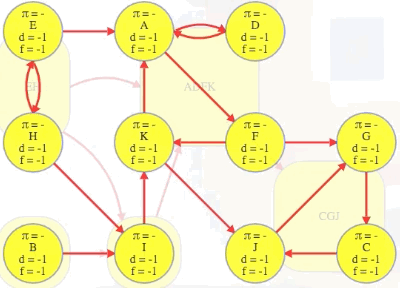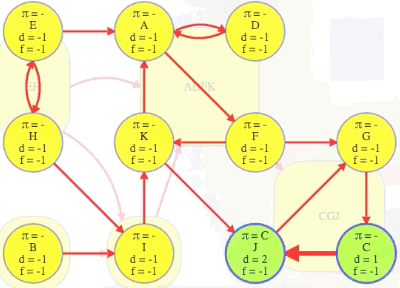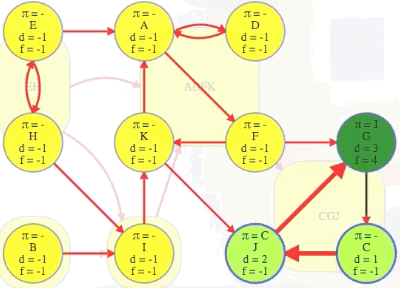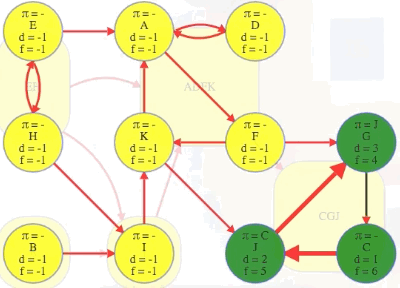
So it would be really nice to search it first and mark it as done.

If we topologically order the underlying component graph, then A's component would be second to last, just before C's component. After we've marked C's component, it would be great if we could next search a vertex from A's component — the search would discover all of its component, but it wouldn't rediscover C's component, which was already discovered when we searched C:

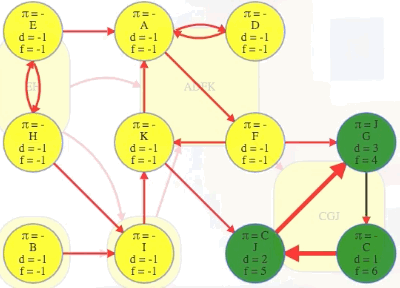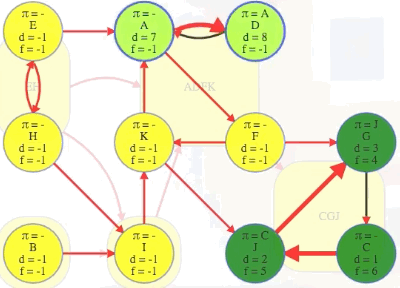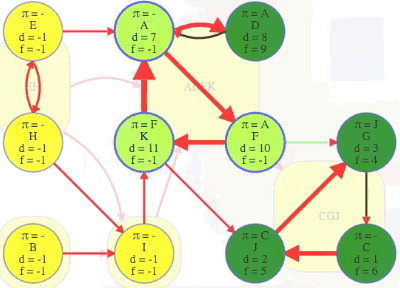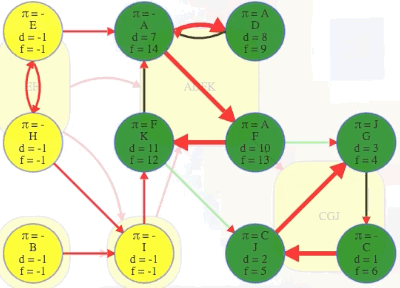
A better order

Let's recap what we wish we could do:

• Magically start from a vertex in a last component.
• Magically continue from a vertex that can go just before that one.

Clever observations

Clever observation 1

The wish list above included some clever observations, but, of course, because we don't know what the components are ahead of time, we don't know how to easily grab a vertex from the topologically last component to search it. Can we figure out some way to topologically sort the underlying component graph even if we don't know the components?

For the two common topological ordering algorithms, Kahn's and DFS, each behaves differently if we run it on a graph with cycles. For any vertex on a cycle or even reachable from a cycle, Kahn's algorithm will never get that vertex's in-degree down to 0 so it will never make it into the ordering. We'd end up with an order that only includes the other vertices (i.e., vertices whose in-degree could eventually be made 0). In the directed graph we've been considering, Kahn's algorithm would return just vertex B. That's obviously not too helpful here.

On the other hand, the DFS-based topological ordering runs DFS and orders the vertices in the reverse order that they finish. That algorithm will order all of the vertices in the graph regardless of cycles; of course, the resultant ordering will not be a topological ordering (because none exists in a graph with cycles), but the ordering is related to the topological ordering of the underlying component graph.

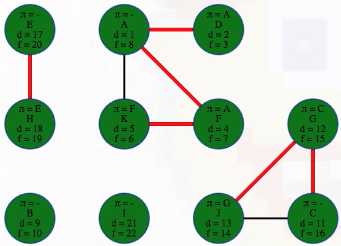
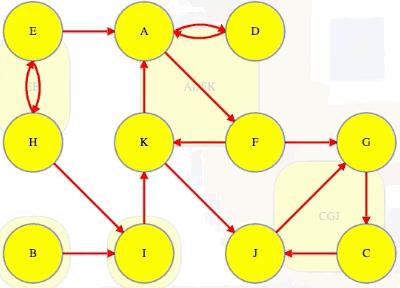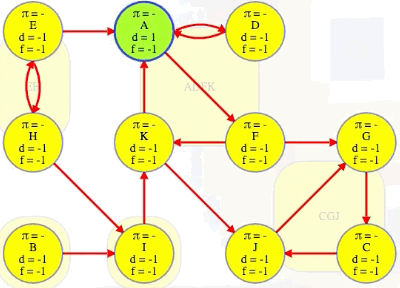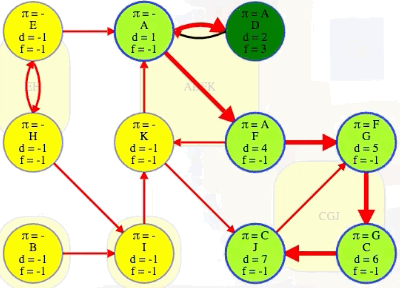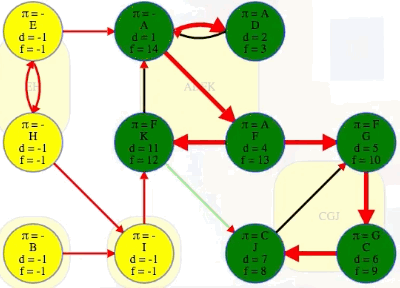
Let's run a DFS on the graph and record the discovery and finish times along with the predecessors and edge classifications (we can use previous work to do this effectively):

Loading...

Output

Click "Run Code" to see the output here

Running DFS on our directed graph, using alphabetical order for top-level calls as well as neighbor visits, yields the following (formatted manually for ease of reference):

""" 

(   A   B  C  D   E   F   G   H   I  J   K
  [ 1, 15, 6, 2, 19,  4,  5, 20, 16, 7, 11],  # discovered
  [14, 18, 9, 3, 22, 13, 10, 21, 17, 8, 12],  # finished
  [-1, -1, 6, 0, -1,  0,  5,  4,  1, 2,  5],  # predecessors
  {                                           # edge classifications
    ('A', 'D'): 'treeEdge',
    ('D', 'A'): 'backEdge',
    ('A', 'F'): 'treeEdge',
    ('F', 'G'): 'treeEdge',
    ('G', 'C'): 'treeEdge',
    ('C', 'J'): 'treeEdge',
    ('J', 'G'): 'backEdge',
    ('F', 'K'): 'treeEdge',
    ('K', 'A'): 'backEdge',
    ('K', 'J'): 'crossEdge',
    ('B', 'I'): 'treeEdge',
    ('I', 'K'): 'crossEdge',
    ('E', 'A'): 'crossEdge',
    ('E', 'H'): 'treeEdge',
    ('H', 'E'): 'backEdge',
    ('H', 'I'): 'crossEdge'
  }
)

"""

This confirms the DFS run on the graph in the video:

That's where the story would end if we just wanted to run a DFS on the whole graph (i.e., finding discovered and finished times for each vertex as well as their predecessors and edge classifications). But in this case, we also want to consider the discovery and finish times for the underlying component super-vertices. The algorithm itself doesn't have any idea what the components are, but we can just cheat and look at them for now.

Importantly, we can define component discovery and finish times as follows:

• discovered: the first time one of its vertices is discovered
• finished: the last time one of its vertices is finished

Note that those two times come from the same vertex within each component:

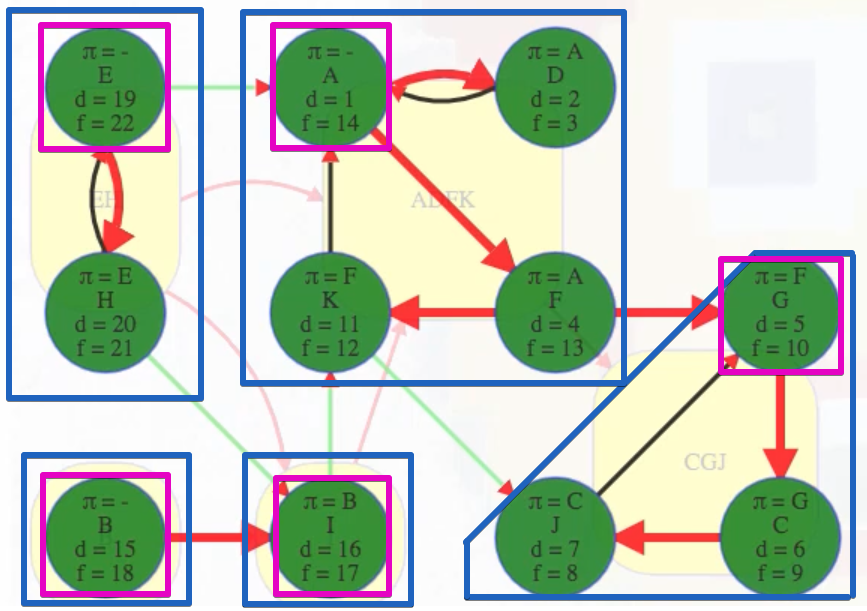
It has to be like that. The first vertex discovered in any component cannot finish being explored until everything it can reach, including all vertices within its component, is finished. Vertices that are discovered later in the component will finish earlier. In the graph above, D is even able to finish before other vertices in the same component have been discovered because it only reaches the rest of the component through vertex A. This brings us to the next clever observation.

Clever observation 2

For the same reason that DFS topological sort works, DFS will finish underlying components in reverse topological order.

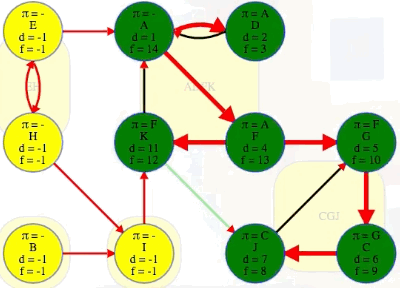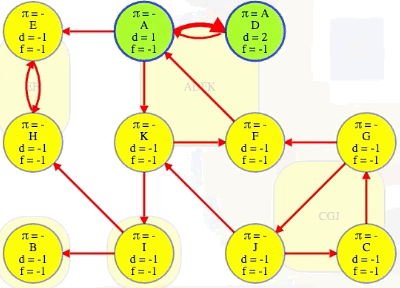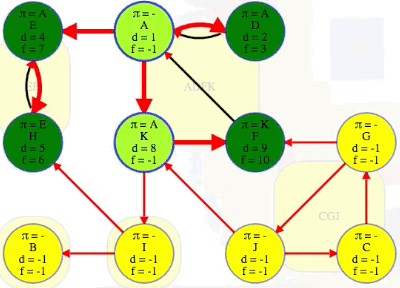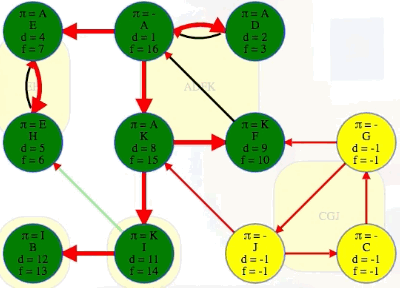
Recall the following details about edge classifications in terms of the graph we've been analyzing:

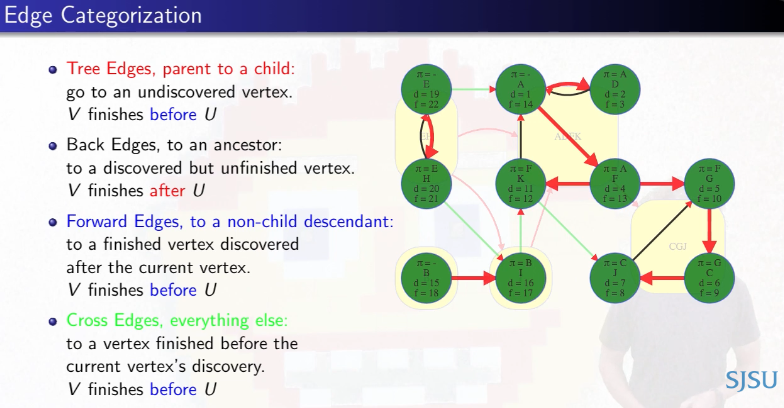
For DFS, tree, forward, and cross edges all have to finish their target vertex before their source vertex. How about back edges? They complete cycles so they all go between two vertices from the same component. Edges between different components have to be something other than a back edge (otherwise the two components could be collapsed into one) — this means that the target vertex and everything it can reach, including that target vertex's entire component, must be finished before the source vertex from the other component is finished. Hence, the source vertex's topologically earlier component has to finish after the target's topologically later component.

Clarification

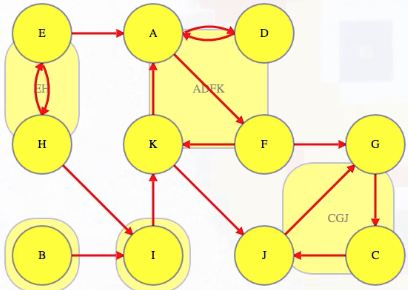
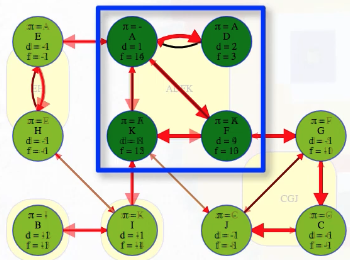
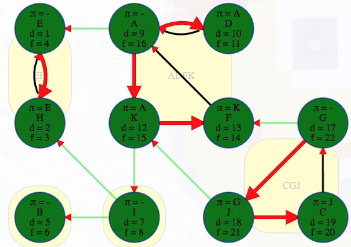
The previous statement is easiest to understand by means of an example from the graph above. Consider the components represented by super vertices ADFK and CGJ. Now consider the tree edge from F to G or the cross edge from K to J that connect these two different components. As expected, neither of these edges are back edges. The edge (F, G) has F as its source vertex and G as its target vertex; similarly, the edge (K, J) has K as its source vertex and J as its target vertex. As noted above, the target vertex and everything it can reach, including the target vertex's entire component, must be finished before the source vertex from the other component is finished:

• (F, G): The source vertex F has finish time 13 while the target vertex G and all the vertices in its component have finish times before the source vertex: G, C, J have finish times 10, 9, 8, respectively, all indicating they are finished before the source vertex F.
• (K, J): The source vertex K has finish time 12 while the target vertex J and all the vertices in its component have finish times before the source vertex: J, G, C have finish times 8, 10, 9, respectively, all indicating they are finished before the source vertex K.

Before remarking on the key takeaway, it's a good time to recall that DFS returns a reverse topological ordering. We can't have a topological ordering for the original graph (because it contains cycles), but, as previously mentioned, the underlying component graph is a DAG which means it must have a topological ordering.

Consider again the result of our first DFS search on the entire graph:

If we ordered components left to right by ascending finish times of their first discovered vertex, then we would have CGJ -> ADFK -> I -> B -> EH:

   CGJ    # G has finish time 10
-> ADFK   # A has finish time 14
-> I      # I has finish time 17
-> B      # B has finish time 18
-> EH     # E has finish time 22

But that is the reverse topological ordering. The proper topological ordering is

EH -> B -> I -> ADFK -> CGJ

The key takeaway is the following:

The source vertex's topologically earlier component has to finish after the target's topologically later component.

This should now be clearer in light of the example edges we've been considering:

The source vertex's topologically earlier component [ADFK in the case of the source vertices F and K for the edges (F, G) and (K, J)] has to finish after the target's topologically later component [CGJ in the case of the target vertices G and J for the edges (F, G) and (K, J)]

Hence, a component that finishes later actually comes earlier in the final non-reversed topological ordering.

But we still don't know what the components are! Nonetheless, running DFS still tells us something about their topological order anyway (i.e., topological order of the components, not the vertices of the original graph itself). Our goal was to learn enough about the underlying component graph's topological order to grab a vertex from the topologically last component, namely C's component in the example graph we've been considering. But from the finish times we've obtained, it still seems hard to do this effectively. In our graph, for example, vertex D finishes first, but its component is in the middle somewhere. The topologically last component finishes first at time 10 for vertex G, but that's hidden from us because we don't know the components ahead of time, and G isn't the first vertex to finish — vertex D is. Without knowing the components, the finish times don't actually help us in identifying a vertex from the topologically last component, which finishes first.

Clever observation 3

However, it's easy for us to promise that E's component finishes last because E itself finishes last. Hence, E's component can go topologically first.

Let's save vertices in the order of their reverse finish times like DFS topological sort does:

It would be nice to find and delete that entire first component and continue on similar to what we did while developing Kahn's algorithm. But how do we delete it if we don't know where it starts and ends? Unlike taking a vertex in the topologically last component (i.e., CGJ), if we search a vertex in the topologically first component (i.e., EH), then we might search other components too (e.g., I and ADFK). In the directed graph previously pictured, searching E would discover everything except B. This brings us to our last clever observation.

Clever observation 4

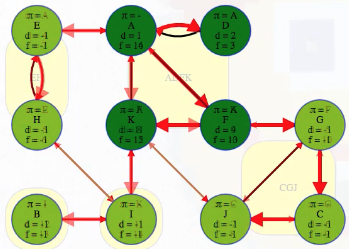
Let $G$ denote the original graph (pictured below to the left). Now let's reverse $G$ to obtain $G^R$; that is, reverse the direction of all edges in $G$ to obtain $G^R$ (pictured below to the right):

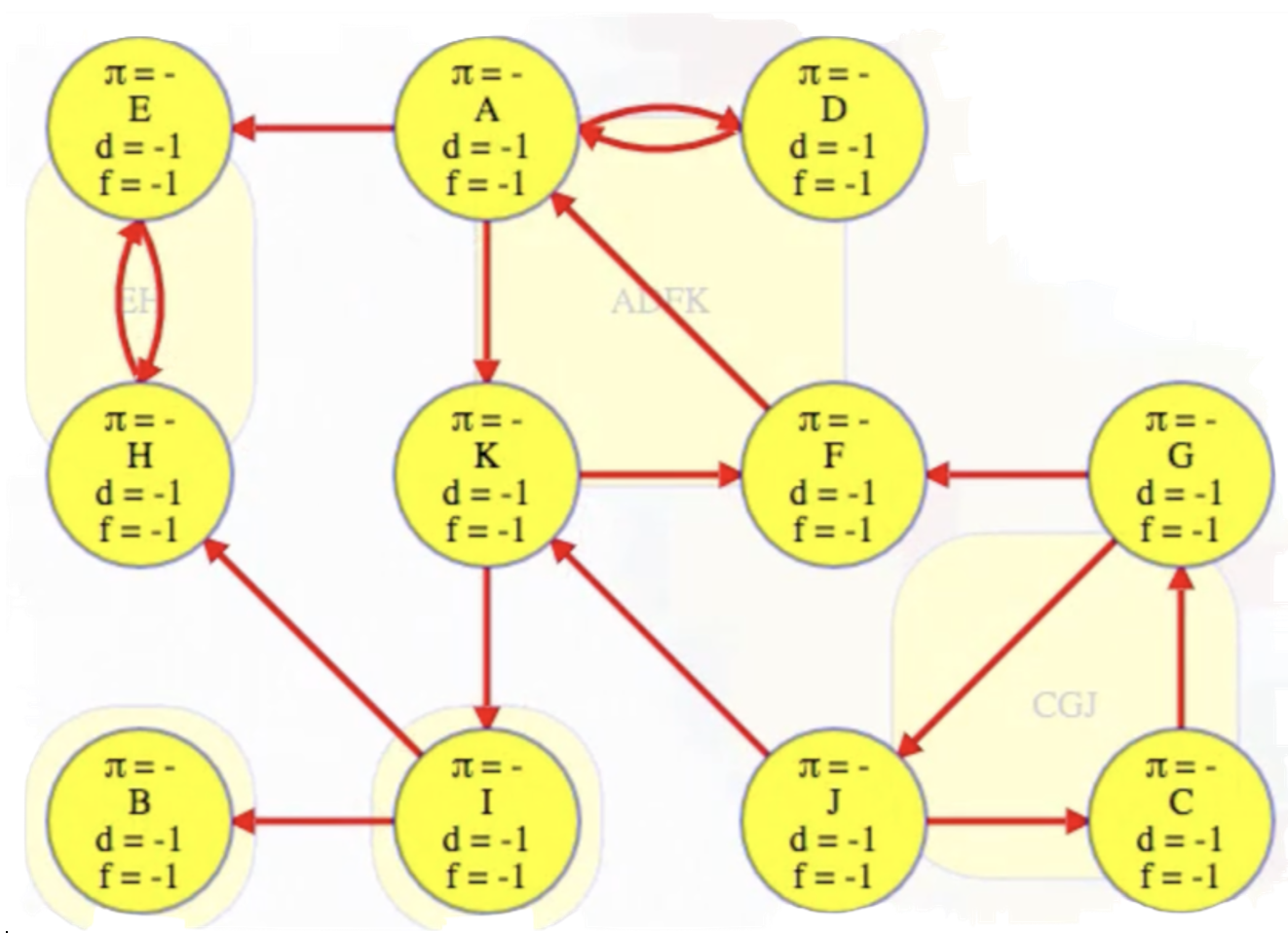
Note how the strongly connected components remain as they were. Nothing changed (in terms of the SCCs). Any two vertices that were on a cycle in $G$ are still on a cycle in $G^R$ — the cycle just goes the other way. But the edges in the underlying component graph now go in the opposite direction.

The topologically first component, EH, that couldn't be reached by any other component in $G$, it now can't reach any other component in $G^R$ — it is now topologically last in $G^R$. So we can grab vertex E, which we know is in the topologically last component in the reversed graph, and search it:

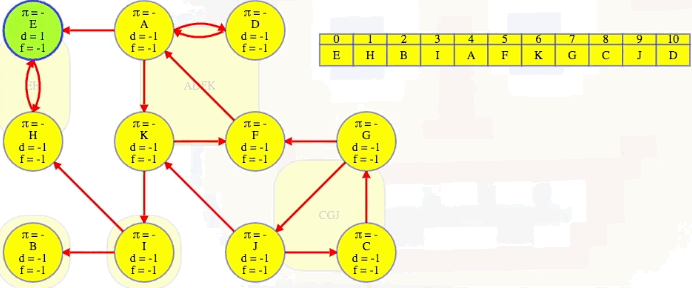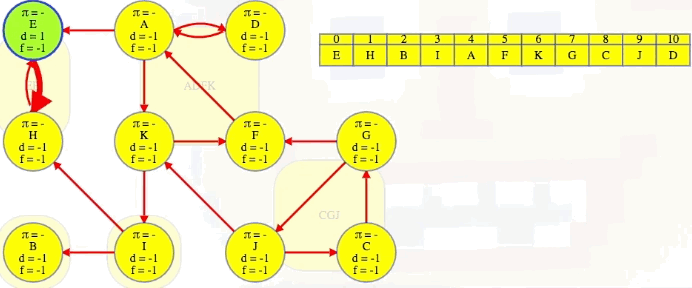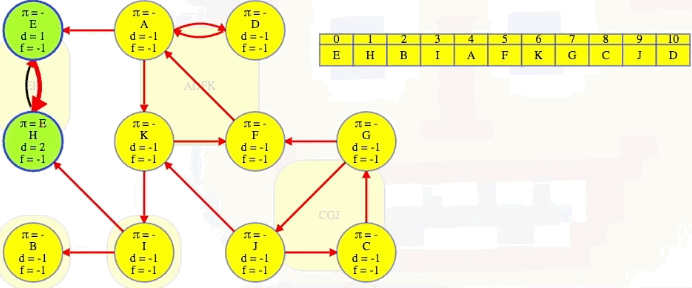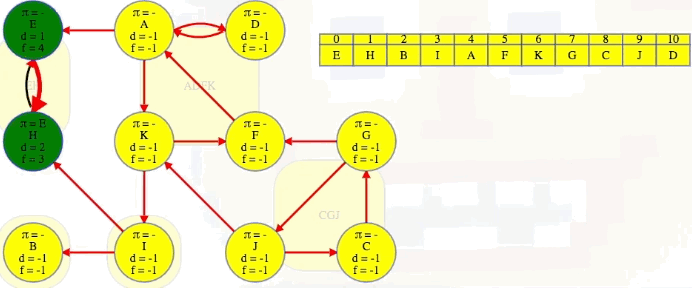
Bang! We just discover its entire strongly connected component:

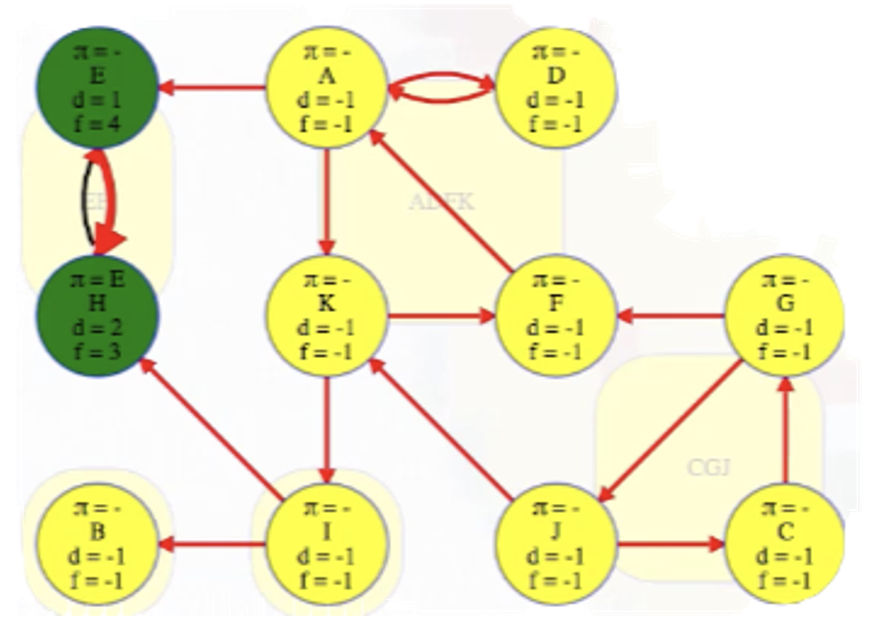
It has no other outgoing edges to other components in $G^R$. Conveniently, the vertex order we saved from our DFS on $G$, the original graph, now lists vertices from the topologically latest components of the reversed graph first:

We use that order to search for components in $G^R$, and we don't need to delete them from the graph to continue. DFS will mark all vertices in E's component as explored, and then we can just continue top-level searches from the other vertices using the next latest finish time from our saved vertex order.

Continuing our search, we go to H next, but H is already discovered so DFS will ignore it, which is good, because we already know its component! The next vertex we run into that we haven't already discovered is B (i.e., going by the vertex order produced by the first DFS of $G$). Its component has the second latest finish time so it can be topologically second to last, just before E's component, in the reversed underlying component graph (or second in the original underlying component graph):

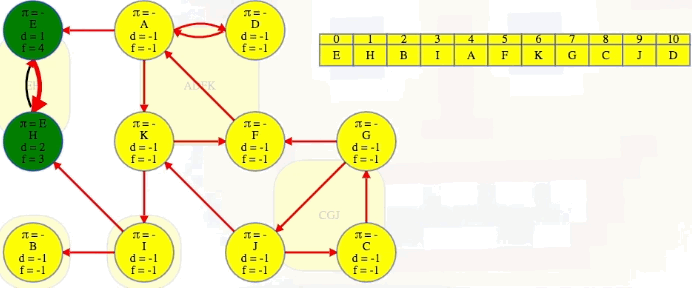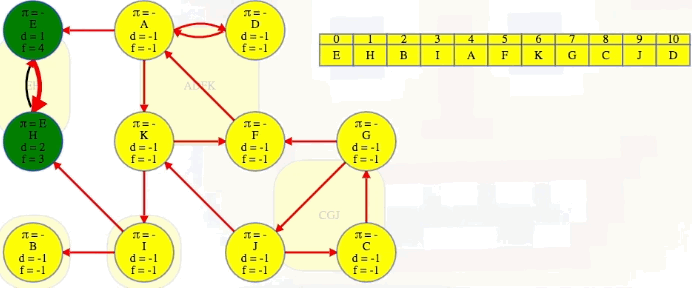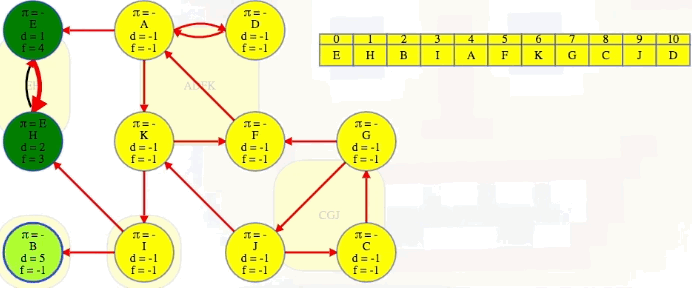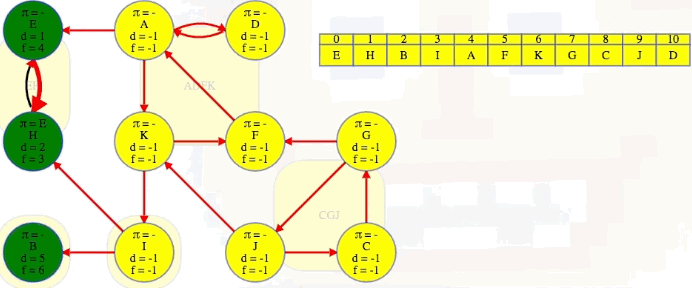
Vertex B doesn't have any outgoing edges in the reverse graph, but the next vertex, I, does. It has edges to both E and B's components, but we already know what those components are. We can't rediscover them:

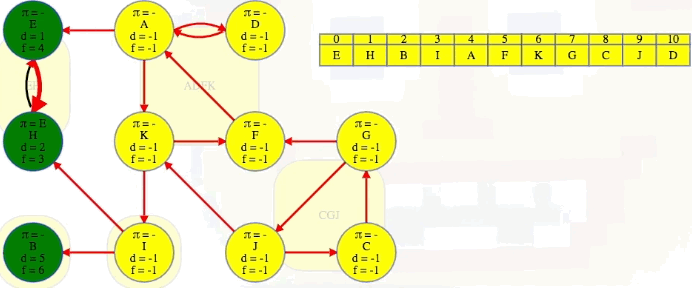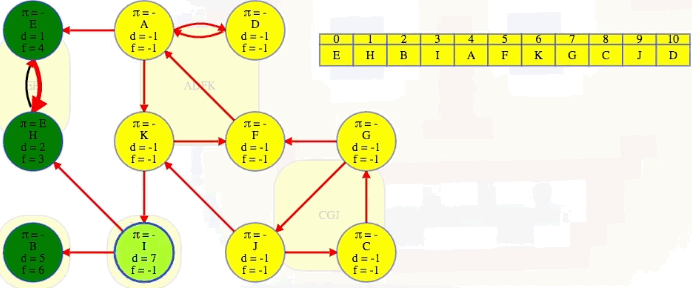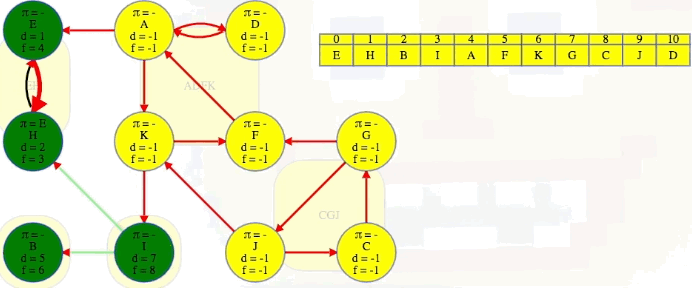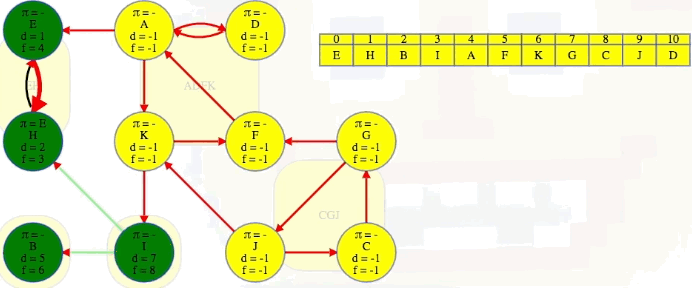
We finish the second DFS on $G^R$, the reversed graph, taking vertices in the reverse order that they finished the initial DFS on $G$, the original graph. Every time we come across a new top-level vertex that hasn't been previously discovered, it will discover its strongly connected component:

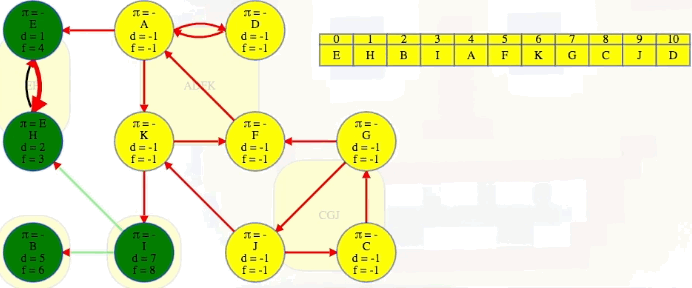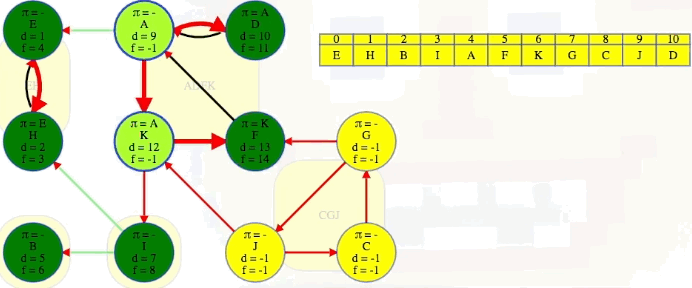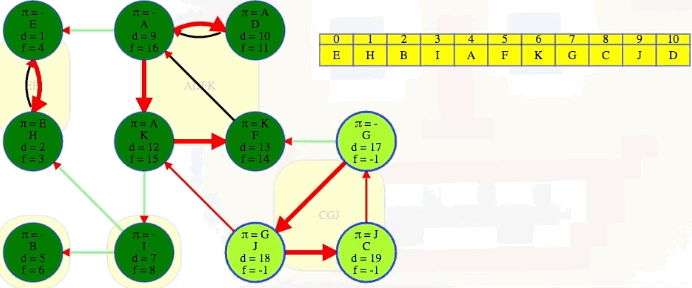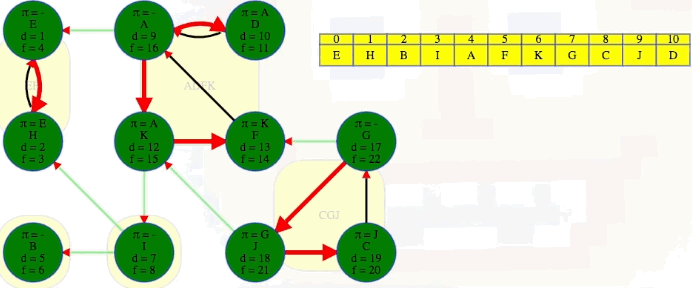
The animation above shows how each strongly connected component is discovered in proper topological order during the second DFS run on $G^R$:

EH -> B -> I -> ADFK -> CGJ

The conclusion of the second DFS is shown below for ease of reference:

The last part of the algorithm, where we run DFS on $G^R$, looks just like discovering components in an undirected graph using DFS except we need to do our top-level searches in the specific order given from the earlier DFS; that is, in the animation shown above, note how top-level calls are not executed in alphabetical order but in the reverse order found by the first DFS on $G$. When we finish, the top-level searches that found something, namely E, B, I, A, and G, have no parent nodes (each discovered its own component):

""" 

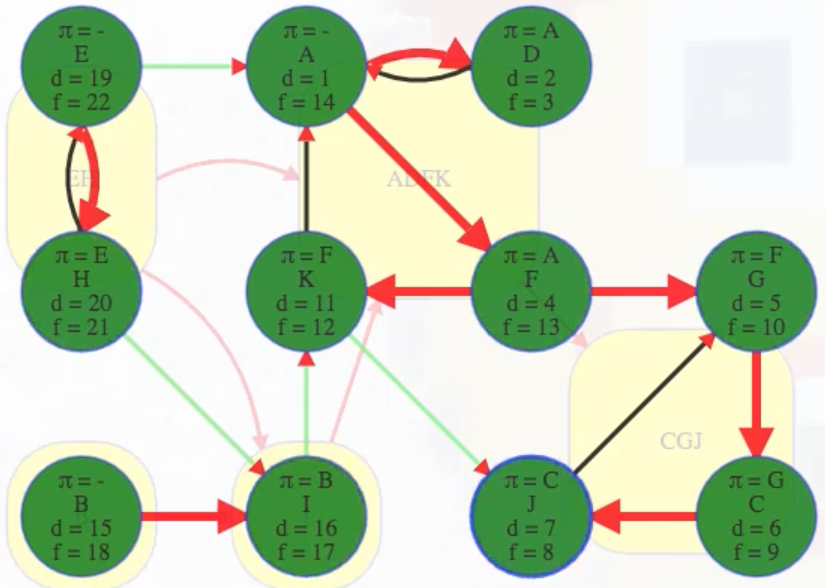
(   A   B   C   D   E   F   G  H   I   J   K
  [ 9,  5, 19, 10,  1, 13, 17, 2,  7, 18, 12],  # discovered 
  [16,  6, 20, 11,  4, 14, 22, 3,  8, 21, 15],  # finished
  [-1, -1,  9,  0, -1, 10, -1, 4, -1,  6,  0],  # predecessors (-1 indicates no parent)
  {                                             # edge classifications
    ('E', 'H'): 'treeEdge', 
    ('H', 'E'): 'backEdge', 
    ('I', 'B'): 'crossEdge', 
    ('I', 'H'): 'crossEdge', 
    ('A', 'D'): 'treeEdge', 
    ('D', 'A'): 'backEdge', 
    ('A', 'E'): 'crossEdge', 
    ('A', 'K'): 'treeEdge', 
    ('K', 'F'): 'treeEdge', 
    ('F', 'A'): 'backEdge', 
    ('K', 'I'): 'crossEdge', 
    ('G', 'F'): 'crossEdge', 
    ('G', 'J'): 'treeEdge', 
    ('J', 'C'): 'treeEdge', 
    ('C', 'G'): 'backEdge', 
    ('J', 'K'): 'crossEdge
  }
)

"""

The DFS forest shows the components with each tree being one component. All edges from one component to another are cross edges:

(A, E)  # connects ADFK to EH
(I, H)  # connects I to EH
(I, B)  # connects I to B
(G, F)  # connects CGJ to ADFK
(J, K)  # connects CGJ to ADFK

That isn't by chance. The only edge that can go between components in that final search is a cross edge because, in the reversed graph, each component is explored and finished before any other component has a chance to accidentally discover it by another edge. There can also be cross edges from within a component, but all edges between components will definitely be cross edges. Tree, back, and forward edges all have to go between two vertices in the same component (the fact that there aren't any forward edges in the sample graph we've been analyzing is simply due to the nature of our sample graph).

End result

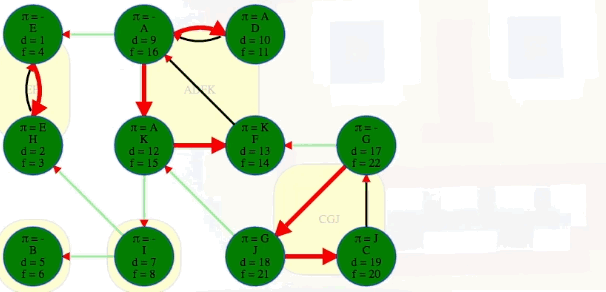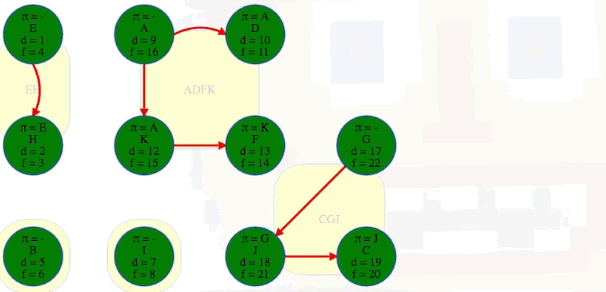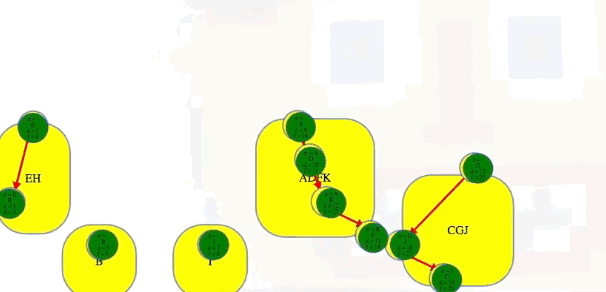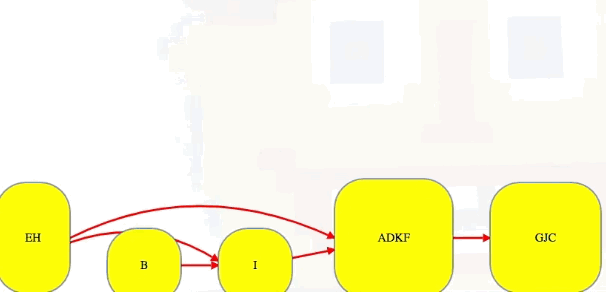
The end result of using all of our clever observations is not only identifying all strongly connected components in the graph but also identifying them in topological order:

Summary of clever observations

Let's briefly recap the clever observations that have gotten us to this point:

• Clever observation 1: SCCs would be easier to find in reverse topological order for the underlying component graph.
• Clever observation 2: DFS completes the underlying components in reverse topological order.
• Clever observation 3: The component of the last vertex to finish can be topologically first.
• Clever observation 4: $G^R$ has the same underlying SCCs as $G$ (in topologically reversed order). The saved DFS order from $G$ touches $G^R$ components in a legal reverse topological order.

Efficient algorithm

The clever observations above give us an efficient algorithm for identifying the SCCs of a graph (and in topological order):

1. Run DFS on $G$ and save the vertex order list by decreasing finish time (finds finish times of unknown components in topological order)
2. Find $G^R$, the reverse graph of $G$ ($G^R$ has the same components but reverses their topological ordering)
3. Run DFS on $G^R$, using the order from step 1 for the top-level calls (finds components in $G^R$ in reverse topological order)

Each successful top-level search discovers a component. Each phase takes time linear in the size of the graph: $\Theta(|V| + |E|)$. So the entire algorithm has linear total runtime: $\Theta(|V| + |E|)$.

In some rough sense, the first DFS on $G$ gives us a topological order for the underlying component graph, and that order is the only thing we need from that first search. The second DFS on $G^R$ helps us discover and mark components in topological order (like when we used Kahn to identify individual vertices in topological order). It looks similar to our original inefficient way to just find one strongly connected component, but now we don't have to take any set intersections.

Full example

Let's go through a full example to see exactly how the efficient algorithm works.

1. Run DFS(G), and save the vertex list by decreasing finish time: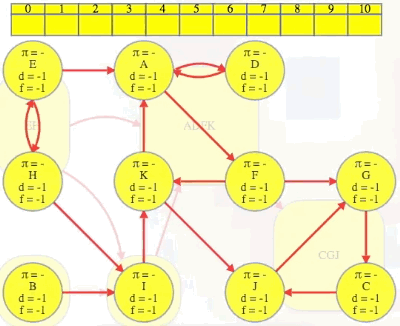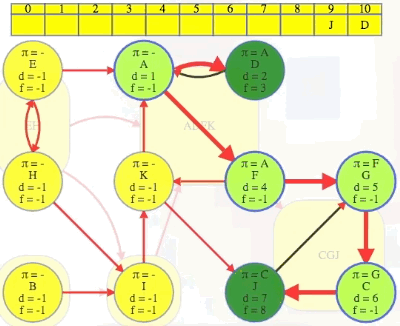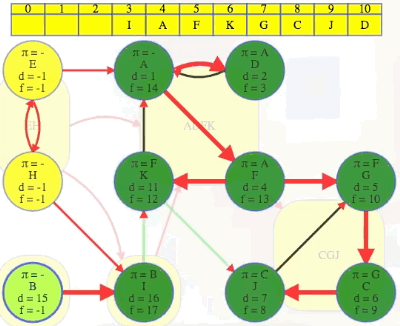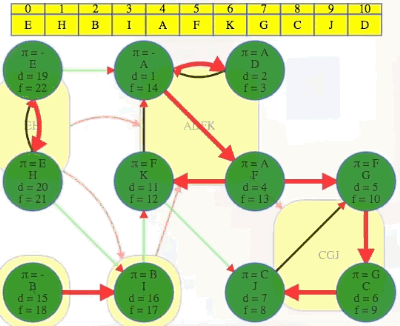

   

   Above, we run the first DFS on $G$, saving vertices in order of reverse finish time (i.e., D finishes first so it goes last in the vertex list, ... , E finishes last so it goes first in the vertex list).

2. Find $G^R$, the reverse of $G$.

3. Run DFS(G^R), and use the order from step 1 one above for the top-level calls on each vertex (the animation below begins where the animation for step 1 ended):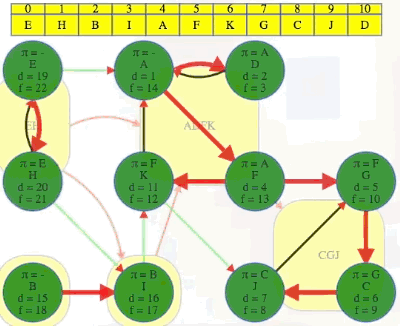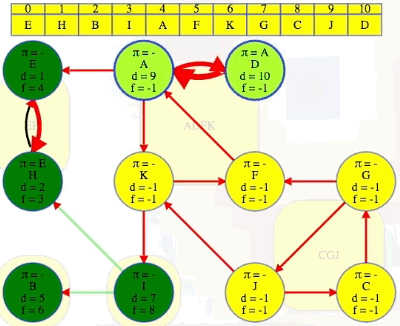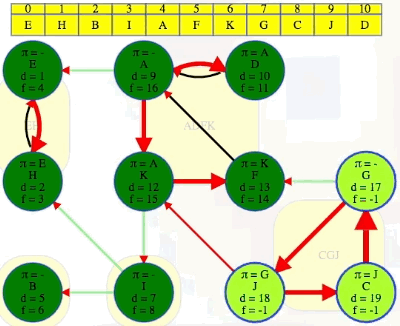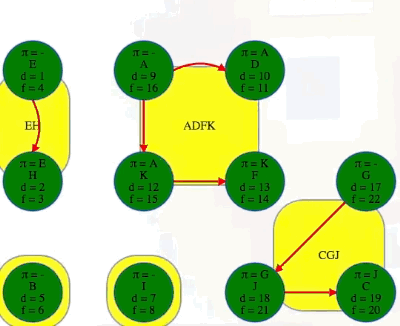

   

   Above, we ran DFS on $G^R$, the reverse graph of $G$ obtained in step 2. Each time we performed a top-level search on a vertex that hadn't yet been discovered, say x, every vertex discovered and finished in that search is in the same component as x. The vertex list found in step 1 stipulates we execute top-level DFS calls on $G^R$ in the following order: E, H, B, I, A, F, K, G, C, J, D:

   $$\underbrace{\texttt{E}}_{\substack{\text{DFS}(G^R, E)\\\text{discovers SCC:}\\[0.25em]\texttt{EH}}},\quad \underbrace{\texttt{H}}_{\substack{\text{DFS}(G^R, H)\\\text{H already discovered}}},\quad \underbrace{\texttt{B}}_{\substack{\text{DFS}(G^R, B)\\\text{discovers SCC:}\\[0.25em]\texttt{B}}},\quad \underbrace{\texttt{I}}_{\substack{\text{DFS}(G^R, I)\\\text{discovers SCC:}\\[0.25em]\texttt{I}}},\quad \underbrace{\texttt{A}}_{\substack{\text{DFS}(G^R, A)\\\text{discovers SCC:}\\[0.25em]\texttt{ADFK}}},\quad \underbrace{\texttt{F}}_{\substack{\text{DFS}(G^R, F)\\\text{F already discovered}}},\quad \underbrace{\texttt{K}}_{\substack{\text{DFS}(G^R, K)\\\text{K already discovered}}},\quad \underbrace{\texttt{G}}_{\substack{\text{DFS}(G^R, G)\\\text{discovers SCC:}\\[0.25em]\texttt{GJC}}},\quad \underbrace{\texttt{C}}_{\substack{\text{DFS}(G^R, C)\\\text{C already discovered}}},\quad \underbrace{\texttt{J}}_{\substack{\text{DFS}(G^R, J)\\\text{J already discovered}}},\quad \underbrace{\texttt{D}}_{\substack{\text{DFS}(G^R, D)\\\text{D already discovered}}}$$

   We can see that the root of each DFS tree has the earliest discovery time and the latest finishing time within its component or DFS tree.

After the three steps above, we can then see the components in the order they were discovered, and we can add edges between components to see the full underlying component graph:

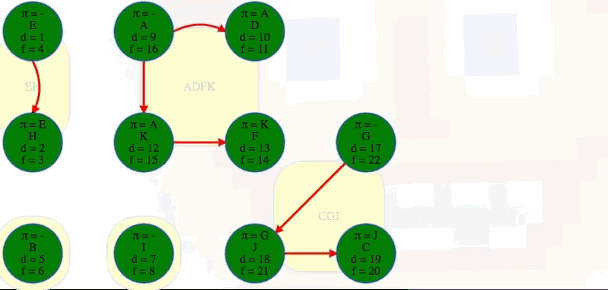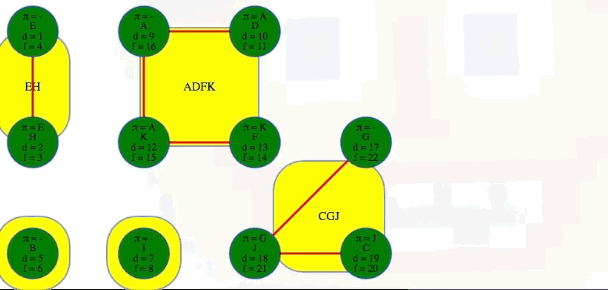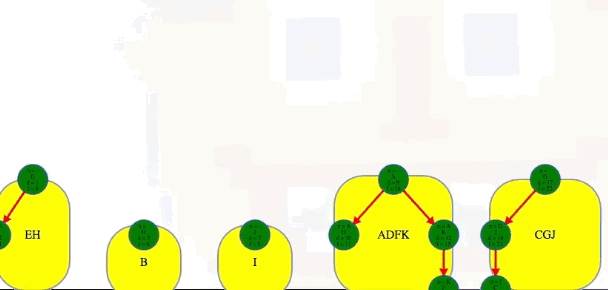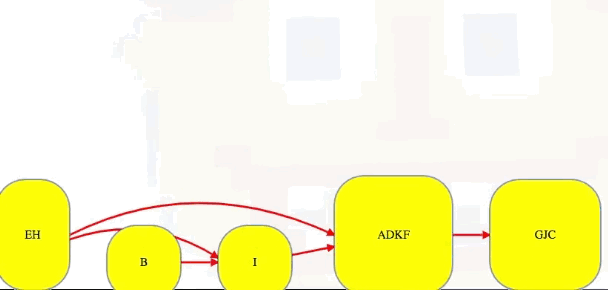
Full example with code (Python)

Loading...

Output

Click "Run Code" to see the output here

The code for Kosaraju's algorithm above, when run on the graph we've been discussing, yields the following output:

[['E', 'H'], ['B'], ['I'], ['A', 'D', 'K', 'F'], ['G', 'J', 'C']]

# EH -> B -> I -> ADKF -> GJC (topological ordering of component graph)

---