The union-find data structure (with attitude)

October 11, 2024

Software Engineer

This post explores the union-find data structure specifically from the vantage point of how we might endeavor going about coming up with the data structure ourselves. A number of templates are then provided.

Attribution

The notes below come from the Algorithms with Attitude YouTube channel, specifically the Disjoint Set playlist right now comprised of only the following video: Disjoint Sets: the Union-Find Data Structure.

There are several sections in this post, accessible in the table of contents on the right, but most of the sections have been listed below for ease of reference and navigation.

The union-find data structure
Implementation (Python)

The union-find data structure

We're going to explore how we might go about coming up with the union-find data structure from scratch. Thus, we will go through a series of steps, each one more refined than the last. The result will be a decently optimized data structure with a few different templates we can use.

Problem definition

The union-find data structure is made to track disjoint sets of objects, which is why sometimes it is simply called a "disjoint set" data structure. But "union-find" is more descriptive because, as we will see, union and find are the methods for this structure where the magic happens.

Whatever the details of our eventual implementation, our data structure needs to be able to make sets with one element each, find out what set any element is in, and union (i.e., combine) two sets into one:

MakeSet(x) creates a new set with x, which is not in any other set.
Find(x) returns a unique identifier for x's set.
Union(x, y) combines the sets x and yif they are distinct, destroying the original sets. (If x and y are in the same set, that set does not get destroyed.) Returns true if and only if x and y were in separate sets and false if they were already in the same set.

That's it. It doesn't do much, but it will end up doing it very well.

Very simple solution

Let's start by trying to just come up with whatever way we can in order to solve the problem. We'll use a dynamic array to hold all information (and we'll initialize it to a big enough size so that it doesn't need to be resized):

If we want to make a new set with some object, such as MakeSet(c), just stick it into the array along with a unique set identifier (we'll just use names here):

Hence, for our example, MakeSet(x) will correspond to adding x, xName to the array. If we execute

MakeSet(c), MakeSet(i), MakeSet(e), MakeSet(a), MakeSet(h), MakeSet(b), MakeSet(f)

then our dynamic array will end up looking something like the following:

If we want to find out if object b is in the same set as object e, then we start from the left and iterate over the array until we find e (i.e., Find(e)), iterate over the array until we find object b (i.e., Find(b)), and if they don't have the same set identifier (i.e., Find(e) != Find(b)), then they aren't in the same set. If they are in different sets, as shown above, then, to take their union (i.e., Union(e, b)), iterate over the entire array and update all objects with e's set identifier of Euclid to have b's set identifier of Blaise. Hence, after the Find(e), Find(b), and Union(e, b) operations, we go from

Even though only one item was updated in this case, we can imagine a sequence of operations where more and more items get updated. For example, if we now ran Union(b, c), then we would need to update all item's with b's set identifier to now have c's set identifier (two updates). And so on.

The following pseudocode serves as a very simple start:

MakeSet(x) {                  # O(1)
    pair.item = x
    pair.ID = UniqueID(x)
    DS.add(pair)
}

Find(x) {                     # O(n)
    for(pair in DS)
        if(pair.item == x)
            return pair.ID
}

Union(x, y) {                 # O(n)
    Xid = Find(x)
    Yid = Find(y)
    if(Xid == Yid) 
        return False
    for(pair in DS)
        if(pair.ID == Xid)
            pair.ID = Yid
    return True
}

This is really simple! But really slow. Adding an item (i.e., MakeSet) takes average constant time, but Find and Union take time $O(n)$ if there are $n$ items. And we have to come up with unique IDs. That's not too hard, but why not just use the objects themselves as IDs? That's easy. Each object is distinct, and sets are distinct (in our example thus far, each object has been a single distinct letter while its set identifier was a name). So if each set has one object that it uses as its representative, then that works. For example,

would become

Of course, we aren't copying the object. We're keeping a reference to it so the array only needs to hold two references for each item in any set (below, we've changed all instances of pair.ID to pair.rep):

MakeSet(x) {                  # O(1)
    pair.item = x
    pair.rep = UniqueID(x)
    DS.add(pair)
}

Find(x) {                     # O(n)
    for(pair in DS)
        if(pair.item == x)
            return pair.rep
}

Union(x, y) {                 # O(n)
    Xid = Find(x)
    Yid = Find(y)
    if(Xid == Yid) 
        return False
    for(pair in DS)
        if(pair.rep == Xid)
            pair.rep = Yid
    return True
}

Improving find to O(1)

How can we speed things up? There are a few things we could do, but it also depends on what we're putting into the set. Are we putting objects into the set that we can mess around with (i.e., can we store references in the objects?)? For this data structure, the assumption is that we can. This won't be a black box data structure like a linked list or array list — we can use those without having direct access to the internals of whatever we're storing. Here, we will modify the objects themselves to hold information (e.g., like how we might write a variable like discovery_status to a vertex of a graph while searching it). Once we have that, we can store a reference to the set representative right in the object itself.

The code gets really simple:

MakeSet(x) {                  # O(1)
    x.rep = x
    DS.add(x)
}

Find(x) {                     # O(1)
    return x.rep
}

Union(x, y) {                 # O(n)
    if(x.rep == y.rep)
        return False
    for(z in DS)
        if(z.rep == x.rep)
            z.rep = y.rep
    return True
}

The Find operation now is really trivial. We just return the representative from the object in constant time. Union, however, still takes linear time in the entire set of objects, but the code and the other runtimes are great.

Improving union to O(lg n)

What can we do to speed up Union? It seems pretty wasteful to go through the entire set of all objects to look for those in just one set. We could keep a list for each set and walk through it to update that set when we call Union (i.e., so far, if x and y did not have the same representative, then calling Union(x, y) would result in iterating over the entire array to find elements whose representative was x in order to change the representative to y; what if, instead of iterating over the entire array, we just iterated over xList, a list of all items we know have x as their representative):

MakeSet(x) {                  # O(1)
    x.rep = x
    x.list = new List(x)
    DS.add(x)
}

Find(x) {                     # O(1)
    return x.rep
}

Union(x, y) {                 # O(|x's set|)
    if(x.rep == y.rep)
        return False
    xList = x.rep.list
    for(z in xList)
        z.rep = y.rep
    y.rep.list.Append(xList)
    x.rep.list = y.rep.list
    return True
}

The list for a set would start with just one item, and when we call Union we append one list to the other. We could use a linked list or a dynamic array. Linked lists will take time proportional to set x's size. Dynamic arrays may sometimes take longer when they have to be resized, but, on average, they have the same asymptotic bounds, probably with better constants even though the linked list append takes only constant time.

Let's take a closer look at the code above. What's the dynamic array doing for us? We add to it, but we never use or look at it. It's a vestigial organ, and we can evolve to get rid of it.

Right now the time complexity of Union(x, y) is the size of x's set, |x's set|, due to the following (lines 14-16 above):

# ...
    xList = x.rep.list
    for(z in xList)
        z.rep = y.rep
# ...

This looks like it could be an area for improvement; specifically, the above is not as efficient as it could be when |x's set| > |y's set|. This suggests we should potentially modify Union(x, y) to union x and y not by the order of arguments to Union but by the size of the sets x and y (i.e., union by size):

MakeSet(x) {                  # O(1)
    x.rep = x
    x.list = new List(x)
}

Find(x) {                     # O(1)
    return x.rep
}

Union(x, y) {                 # O(|smaller set|)
    if(x.rep == y.rep)
        return False
    if(x.rep.list.size() > y.rep.list.size())
        tmp = x
        x = y
        y = tmp
    xList = x.rep.list
    for(z in xList)
        z.rep = y.rep
    y.rep.list.Append(xList)
    x.rep.list = y.rep.list
    return True
}

Unioning by size makes more sense. For example, previously, if we called Union(x, y), where, say, the size of x was 8 and the size of y was 4, we'd go through the entire set of 8 elements to fix their representatives. But how does that make any sense? When Amazon acquired Twitch, it wasn't an even merge — they didn't flip a coin to see which company would absorb the other. The big company absorbed the small company.

That's what we do above. We let the big set "absord" the smaller set when it comes to merging representatives. Now our union-find data structure is looking a bit better. Let's walk through an example to see how it's behaving now.

Let's start with the sequence of assignments

MakeSet(c), MakeSet(i), MakeSet(e), MakeSet(a), MakeSet(h), MakeSet(b), MakeSet(k), MakeSet(f)

to get

We can effectively visualize Union operations as tree-like nature in the sense that Union(x, y) ends up pointing the smaller set to the larger set. For example, if we run Union(b, e), then

becomes

Let's make some more sets

MakeSet(j), MakeSet(l), MakeSet(g), MakeSet(d)

to expand things a bit:

Running Union(g, i) will result in a similar change as before:

But what happens now if we run Union(b, g)? Well, their set size is the same right now (2) so we'll just end up pointing b's list to g's representative:

But we don't just move over b's list in the manner pictured above — we update every element in b's list to make its representative point to g's representative:

Union(b, g)
    # ...
    bList = b.rep.list
    for(z in bList)
        z.rep = g.rep
    # ...

Hence, the outcome from Union(b, g) can be more accurately represented in the following way (i.e., where each element in b's set, namely b and e, now point directly to g's representative, i):

We can run Union(d, l), Union(a, h), and Union(c, k) to combine things a bit more:

If we run Union(c, d), then we'll get something like we just discussed for Union(b, g), where each of the representatives in c's set (c and k) will now point directly to the representative for d's set (l):

Running Union(f, j) and Union(a, f) will result in a similar change:

We can see how we're now only two Union operations away from all sets having a single representative. Let's run Union(f, i):

If we run Union(a, c), then note how we c's set is smaller than a's set at this point; hence, we'll be shifting set items in the following way:

The end result is that all sets have the same representative:

To recap the process for the example above, if we think about an object x in a set, then every time x's representative gets changed, the size of the set it's in has to at least double (this is because the size of the set absorbing x's set must be at least the size of x's set, which means x's new set will have at least twice as many elements as x's original set). So if there are $n$ total objects, then no object can change its representative more than $\lg n$ times.

For our data structure right now, if there are $n$ objects, $n$ calls to union can't take more than $O(n\lg n)$ time total for $O(\lg n)$ average for each call. That's not bad. But we're two observations away from awesome.

Being lazy

The first is that our data structure is really proactive; that is, if we have 10 things in a set and it merges with a larger set, then we run to every one of those 10 things to tell them they need to update:

# ...
for(z in xList)
        z.rep = y.rep
# ...

Then we run through the list to append one to another just so that we can proactively update every object's representative the next time.

For example, when we previously called Union(a, c) on

this resulted in us going from

But maybe object k doesn't even care what set it's in. And we just keep running up to it to tell it that it has a new representative. That's like doing every problem in a textbook so that it's ready to turn in just in case the teacher asks for us to do that problem for homework. We'll know our stuff really well, but it's not the quickest way to do homework. Relax. Be more lazy.

Don't tell everyone they have a new representative if they don't ask. When a set merges with another, just update the representative of the smaller set to make it reference the representative of the larger set. And don't worry about the other objects in the set. Now they don't reference their representative, but they do reference an object closer to their representative. How does this change our code?

First, we don't have to walk through our list during the update. We just change one representative. Once we do that, we don't use the lists except for their size. So just store their size (don't store the lists)! Now each object just has to keep one reference and a size:

MakeSet(x) {                  # O(1)
    x.rep = x
    x.size = 1
}

Find(x) {                     # O(1)
    return x.rep
}

Union(x, y) {
    if(x.rep == y.rep)
        return False
    if(x.rep.size > y.rep.size)
        tmp = x
        x = y
        y = tmp
    
    x.rep.rep = y.rep
    y.rep.size += x.rep.size

    return True
}

The set is a tree, but objects don't keep track of their children, only the size of their set. It's like if we know we have two kids, but we don't have any idea who they are, and we don't worry about it because we never look for them to tell them anything anyway (sounds bad, but it's illustrative). Now that representatives aren't all proactively updated, we have to fix the Find method:

MakeSet(x) {                  # O(1)
    x.rep = x
    x.size = 1
}

Find(x) {
    if(x != x.rep)
        return Find(x.rep)
    return x
}

Union(x, y) {                 # O(|smaller set|)
    if(x.rep == y.rep)
        return False
    if(x.rep.size > y.rep.size)
        tmp = x
        x = y
        y = tmp
    
    x.rep.rep = y.rep
    y.rep.size += x.rep.size

    return True
}

The set representative knows it's the set representative just like our congressman knows he's our congressman. For anybody else, recursively ask our last known congressman who their congressman is. Finally because we don't have direct links to our representatives, we use Find instead of the direct link we had previously: if(x.rep == y.rep) return False. This gives us the following:

MakeSet(x) {                  # O(1)
    x.rep = x
    x.size = 1
}

Find(x) {                     # O(lg|set size|)
    if(x != x.rep)
        return Find(x.rep)
    return x
}

Union(x, y) {                 # O(1) plus two Find calls
    smaller = Find(x)
    larger = Find(y)

    if(smaller == larger)
        return False

    if(smaller.size > larger.size)
        tmp = smaller
        smaller = larger
        larger = tmp
    
    smaller.rep = larger
    larger.size += smaller.size

    return True
}

We don't need to store lists now, but what about speed? Union makes two calls to Find but otherwise only takes constant time. But this isn't great for Find. The representative can check that it is its own representative in constant time, but other vertices need to walk up that tree to get to the root. Excluding Find, Union is really fast. But Find is slower, and Union calls it so that seems like a bad tradeoff. Find isn't terrible. We still do Union by size so the tree height can't be more than the logarithm of its size. And the code looks clean (partially because we defined Find recursively instead of using a loop).

But the real problem is that Find previously only took constant time, and Union was logarithmic, but we can only have $n - 1$ slow calls to Union with $n$ items. After that, everything was in one set. Now we can have lots of slow calls to Find.

Suppose we have the following sequence of calls:

MakeSet(c), MakeSet(i), MakeSet(e), MakeSet(a), MakeSet(h), MakeSet(b), MakeSet(k), MakeSet(f),
Union(b, e),
MakeSet(j), MakeSet(l), MakeSet(g), MakeSet(d),
Union(g, i), Union(b, g), Union(d, l), Union(a, h), Union(c, k), Union(c, d), Union(f, j), Union(a, f), Union(f, i), Union(a, c)

There are 12 sets, and 12 - 1 = 11 meaningful calls to Union (i.e., calls that result in two sets being merged). This gives us a tree structure that looks like the following:

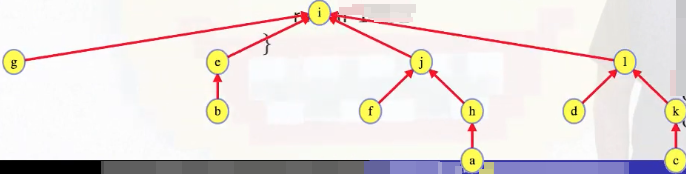
Not being stupid

Using the tree structure above as an example, how can we have a lot of slow calls to Find? Well, what if we call Find(a)? Then we walk up some path to the tree root:

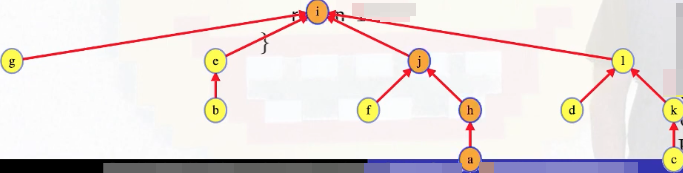
Is that bad? It's not great. But we see the real problem if we try to call Find(a) again:

We repeat the exact same work. That's not just lazy. It's stupid.

We went from being overly diligent, updating every object's representative even if it didn't care, to not even bothering to record and updated representative even after we found it. If we're forced to do the work anyway, then we should save our work. If our congressman loses their election, and we call them to ask them if they're still our representative, then they'll be annoyed, If we call them the next day to ask them again, then they'll be pissed.

To find a's representative, we ask every object on the path to the root what their representative is — update them all:

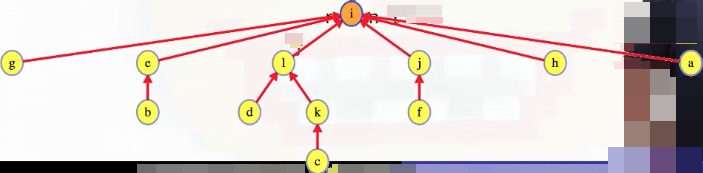
That is, since Find(a) took us along the path a -> h -> j -> i, we end up pointing all of a, h, j to i. It'd be nice if we could call such trees "lazy but not stupid trees", but what we've just described is called path compression instead. And, to be fair, this terminology does make sense. After all, if we traversed the path a -> h -> j -> i when calling Find(a), and then we subsequently have a -> i, h -> i, j -> i, then we can see how the path a -> h -> j -> i has basically been "compressed".

Now we can see just how clean recursion can make our code. How do we add path compression to our previous code? We recursively update the representative or parent, and that's it:

MakeSet(x) {                  # O(1)
    x.rep = x
    x.size = 1
}

Find(x) {                     # O(lg|set size|)
    if(x != x.rep)
        x.rep = Find(x.rep)
    return x.rep
}

Union(x, y) {                 # O(1) plus two Find calls
    smaller = Find(x)
    larger = Find(y)

    if(smaller == larger)
        return False

    if(smaller.size > larger.size)
        tmp = smaller
        smaller = larger
        larger = tmp
    
    smaller.rep = larger
    larger.size += smaller.size

    return True
}

We only had to change a couple characters of code. Our MakeSet method looks the same, and we won't see any real difference until Find is called on a non-root vertex. Any call to Find on a non-root vertex will break and reform its link, even if it's to the same node, because if an item isn't the representative, then it automatically reassigns a new representative when we call Find. There is no inherent order for the children (e.g., like there is binary trees) — in this "social dystopia" we've been discussing, remember that the parent doesn't even know who its children are.

The critical observation is that now when we call Find on a deeper vertex, we see its path compressed. For example, suppose we had a series of MakeSet and Union operations that led to the following tree structure:

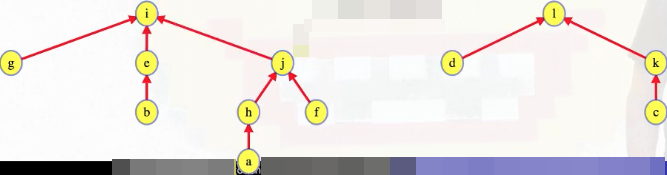
Calling Find on a means we traverse the entire path from a to the root (a -> h -> j -> i):

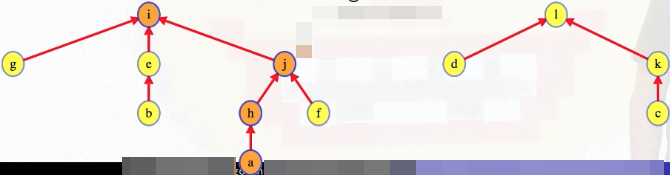
But the path a -> h -> j -> i gets compressed because every representative along the way is updated to point to the root:

Final performance

Path compression keeps the trees from getting tall. Trees can still get to be logarithmic in depth, but for that to happen we have to keep taking the Union of roots or something near the root. Find now takes time proportional to the depth of the node so those unions are really quick. Basically, to get a Find operation that takes logarithmic time, we have to first get a whole bunch of Unions and Finds that are fast. So the average time per operation will be much better than logarithmic. How much better? If we have $n$ objects, then the average time per operation will grow strictly asymptotically slower than $o(\lg^* n)$ . More precisely, it grows like the inverse Ackermann function: $\Theta(\alpha(n))$ .

In [21] and other texts, union by rank is preferred over union by size. They both have the same asymptotic bounds though. If we didn't have path compression, then the rank of a set would just be its height. But once we add path compression, keeping track of height can hurt our efficiency. So rank is basically what the height would have been on the same operations if there were never any path compression.

Implementation (Python)

The approach for establishing a union-find data structure described in this post (and the linked video) is union by size. If we want to actually implement this data structure ourselves, then we immediately run into a problem: how many vertices/sets are there? Is the number fixed or can it be dynamic? Our answer to this question will influence how we go about trying to implement the data structure.

If the number of vertices is fixed, then we can initialize an array of a specific size to hold information about each vertex. Furthermore, we can bundle in the implied MakeSet operations when we initialize the union-find data structure (i.e., for each vertex we can go ahead and assign its root as well as its size).

But what options do we have in scenarios where maybe the number of vertices is not known in advance, but we would still like to make use of the union-find data structure?

We can use hash maps! But note how this now becomes much more of a data structure design problem in terms of how the different methods should behave:

make_set(x): If x is already in the data structure, then should its information be overwritten? Probably not.
find(x): If x is not yet in the data structure, then should this method throw an error? Maybe.
union(x, y): If one or both of the elements is not in the data structure, then should this method throw an error? Maybe.
connected(x, y): If one or both of the elements is not in the data structure, then should this method throw an error? Maybe.

Things can get a bit messy if we start adding a bunch of membership checks. What if we just call make_set(x) whenever find(x) is called (find is called when it itself is called, when union is called, and when connected is called)? If x is already in the data structure, then we can modify make_set to avoid making an update; otherwise, make_set is a constant time operation that can ensure we never encounter any access errors.

As we'll see in the templates below, code alterations are very minor for going from a fixed number of vertices to a dynamic number of vertices: use hash maps instead of arrays with a pre-defined number of elements, add the make_set method, and then add a make_set call at the beginning of the find method. That's it.

For the sake of clarity, the template for implementing the union-find structure with a fixed number of vertices, which is probably the most preferable form, is provided below with commented code (the other templates do not have a bunch of comments in the code):

# T: O(α(n)) per operation; S: O(n)
class UnionFind:
    # MakeSet operations implicit for graph with n vertices (n = num_vertices)
    def __init__(self, num_vertices):
        self.root = [i for i in range(num_vertices)]
        self.rank = [0] * num_vertices

    # path compression: make the representative of x point directly to the root
    def find(self, x):
        if self.root[x] != x:
            self.root[x] = self.find(self.root[x])
        return self.root[x]

    # return False if x and y are in the same set; otherwise,
    #   union by rank: attach the shorter tree under the taller one;
    #   if ranks are equal, update the rank of the tree being attached to;
    #   return True once x and y have been unioned into the same set
    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return False
        
        rank_x = self.rank[root_x]
        rank_y = self.rank[root_y]
        if rank_x > rank_y:
            self.root[root_y] = root_x
        elif rank_x < rank_y:
            self.root[root_x] = root_y
        else:
            self.root[root_y] = root_x
            self.rank[root_x] += 1
            
        return True

    # utility method to quickly determine if x and y are connected
    def connected(self, x, y):
        return self.find(x) == self.find(y)

Union by size

Fixed number of vertices

Union by size (not dynamic)
# T: O(α(n)) per operation; S: O(n)
class UnionFind:
    def __init__(self, num_vertices):
        self.root = [i for i in range(num_vertices)]
        self.size = [1] * num_vertices

    def find(self, x):
        if self.root[x] != x:
            self.root[x] = self.find(self.root[x])
        return self.root[x]

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return False
        
        if self.size[root_x] > self.size[root_y]:
            root_x, root_y = root_y, root_x
            
        self.root[root_x] = root_y
        self.size[root_y] += self.size[root_x]
            
        return True

    def connected(self, x, y):
        return self.find(x) == self.find(y)

Dynamic number of vertices

Union by size (dynamic)
# T: O(α(n)) per operation; S: O(n)
class UnionFind:
    def __init__(self):
        self.root = {}
        self.size = {}

    def make_set(self, x):
        if x not in self.root:
            self.root[x] = x
            self.size[x] = 1

    def find(self, x):
        self.make_set(x)
        if self.root[x] != x:
            self.root[x] = self.find(self.root[x])
        return self.root[x]

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return False
        
        if self.size[root_x] > self.size[root_y]:
            root_x, root_y = root_y, root_x
            
        self.root[root_x] = root_y
        self.size[root_y] += self.size[root_x]
            
        return True

    def connected(self, x, y):
        return self.find(x) == self.find(y)

Union by rank

Fixed number of vertices

Union by rank (not dynamic)
# T: O(α(n)) per operation; S: O(n)
class UnionFind:
    def __init__(self, num_vertices):
        self.root = [i for i in range(num_vertices)]
        self.rank = [0] * num_vertices

    def find(self, x):
        if self.root[x] != x:
            self.root[x] = self.find(self.root[x])
        return self.root[x]

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return False
        
        rank_x = self.rank[root_x]
        rank_y = self.rank[root_y]
        if rank_x > rank_y:
            self.root[root_y] = root_x
        elif rank_x < rank_y:
            self.root[root_x] = root_y
        else:
            self.root[root_y] = root_x
            self.rank[root_x] += 1
            
        return True

    def connected(self, x, y):
        return self.find(x) == self.find(y)

Dynamic number of vertices

Union by rank (dynamic)
# T: O(α(n)) per operation; S: O(n)
class UnionFind:
    def __init__(self):
        self.root = {}
        self.rank = {}
        
    def make_set(self, x):
        if x not in self.root:
            self.root[x] = x
            self.rank[x] = 0

    def find(self, x):
        self.make_set(x)
        if self.root[x] != x:
            self.root[x] = self.find(self.root[x])
        return self.root[x]

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return False
        
        rank_x = self.rank[root_x]
        rank_y = self.rank[root_y]
        if rank_x > rank_y:
            self.root[root_y] = root_x
        elif rank_x < rank_y:
            self.root[root_x] = root_y
        else:
            self.root[root_y] = root_x
            self.rank[root_x] += 1
            
        return True

    def connected(self, x, y):
        return self.find(x) == self.find(y)

Comparing union by rank vs. union by size

Generally speaking, there's not much variation in the way the find method of the union-find data structure is implemented (path compression is always used for the sake of optimality), but there are at least two notable variations in how the union method may be implemented, namely by rank and by size. Many sources (e.g., Cormen et al.) use union by rank, but other sources (e.g., the video on which this post is based) use union by size.

What's the difference? Let's compare the union by rank and union by size approaches side by side (differences highlighted):

Union by rank
# T: O(α(n)) per operation; S: O(n)
class UnionFind:
    def __init__(self, num_vertices):
        self.root = [i for i in range(num_vertices)]
        self.rank = [0] * num_vertices

    def find(self, x):
        if self.root[x] != x:
            self.root[x] = self.find(self.root[x])
        return self.root[x]

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return False
        
        rank_x = self.rank[root_x]
        rank_y = self.rank[root_y]
        if rank_x > rank_y:
            self.root[root_y] = root_x
        elif rank_x < rank_y:
            self.root[root_x] = root_y
        else:
            self.root[root_y] = root_x
            self.rank[root_x] += 1
            
        return True

    def connected(self, x, y):
        return self.find(x) == self.find(y)

Union by size
# T: O(α(n)) per operation; S: O(n)
class UnionFind:
    def __init__(self, num_vertices):
        self.root = [i for i in range(num_vertices)]
        self.size = [1] * num_vertices

    def find(self, x):
        if self.root[x] != x:
            self.root[x] = self.find(self.root[x])
        return self.root[x]

    def union(self, x, y):
        root_x = self.find(x)
        root_y = self.find(y)
        if root_x == root_y:
            return False
        
        if self.size[root_x] > self.size[root_y]:
            root_x, root_y = root_y, root_x
            
        self.root[root_x] = root_y
        self.size[root_y] += self.size[root_x]
            
        return True

    
    
    

    def connected(self, x, y):
        return self.find(x) == self.find(y)

The first difference is immaterial: the rank array is initialized with values of 0 to indicate the height of a tree with a single node whereas the size array is initialized with values of 1 to indicate that initialized sets with a single element have a size of 1.

The other highlighted code is where the real differences lie:

By rank: Rank only increases when two trees of the same rank are merged; hence, if a smaller rank tree is merged with a larger rank tree (arguably the usual case), then the rank of the larger tree doesn't change. The upshot is that the rank-based approach is rather conservative in increasing the tree height for union operations.
By size: The size of the tree is always updated during a union operation. The smaller tree's size is added to the larger tree's size, and the height of the tree is not explicitly tracked. Merging trees based on the number of elements helps maintain relatively balanced trees, albeit arguably not quite as well as the rank-based approach, which is why the rank-based approach shows up in more textbooks and different DSA contexts.

The time and space complexity of both approaches is largely the same so it mostly boils down to a preference as to what version you choose to implement.

The union-find data structure​

Problem definition​

Very simple solution​

Improving find to O(1)​

Improving union to O(lg n)​

Being lazy​

Not being stupid​

Final performance​

Implementation (Python)​

Union by size​

Fixed number of vertices​

Dynamic number of vertices​

Union by rank​

Fixed number of vertices​

Dynamic number of vertices​

Comparing union by rank vs. union by size​

The union-find data structure

Problem definition

Very simple solution

Improving find to O(1)

Improving union to O(lg n)

Being lazy

Not being stupid

Final performance

Implementation (Python)

Union by size

Fixed number of vertices

Dynamic number of vertices

Union by rank

Fixed number of vertices

Dynamic number of vertices

Comparing union by rank vs. union by size