Working with arbitrary bases

This post details how to work with arbitrary bases in a positional numeral system (e.g., decimal, binary, etc.). Specifically, this post details how to convert numbers from base 10 to base $b$ in such a way that not only is the whole number portion converted but also the fractional/radix portion as well.

Attribution

Much of the discussion that follows has been taken from [12].

Division Algorithm

The division algorithm, as stated in [14], is as follows:

Let $a$ be an integer and $d$ a positive integer. Then there are unique integers $q$ and $r$, with $0\leq r < d$, such that $a=dq+r$.

In the equality given above, $d$ is called the divisor, $a$ is called the dividend, $q$ is called the quotient, and $r$ is called the remainder.

Arbitrary bases (description)

We recall that to represent a number in a positional numeral system with base $b$ we need basic symbols for the integers zero up through $b - 1$. Even though the base $b = 10$ is such an important part of our culture, the choice of 10 is really quite arbitrary, and other bases have great practical and theoretical importance. If $b\leq 10$, we may use our ordinary digit symbols; thus, for example, we may consider 3012 as a number expressed to base 4 with the basic symbols 0, 1, 2, 3. To make clear that the number is considered as expressed to base 4, we shall write it as $(3012)_4$. When no subscript is written, it will be understood in this treatment that the number is expressed to the ordinary base 10. If $b > 10$, we must augment our digit symbols by some new basic symbols, for we always need $b$ basic symbols. If $b = 12$, therefore, we may take 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, $t$, $e$ for our basic symbols, where $t$ and $e$ are symbols for ten and eleven; for example, we might have $(3t1e)_{12}$.

It is easy to convert a number from a given base to the ordinary base 10. Thus, we have

$$(3012)_4=3(4^3)+0(4^2)+1(4)+2 = 198$$

and

$$(3t1e)_{12}=3(12^3)+10(12^2)+1(12)+11=6647.$$

If we have a number expressed in the ordinary scale, then we may express it to base $b$ as follows. Letting $N$ be the number, we have to determine the integers $a_n, a_{n-1},\ldots, a_0$ in the expression

$$N=a_nb^n + a_{n-1}b^{n-1}+\cdots+a_2b^2+a_1b+a_0,$$

where $0\leq a_i < b$. Dividing the above equation by $b$, we have

$$\frac{N}{b}=a_nb^{n-1}+a_{n-1}b^{n-2}+\cdots+a_2b+a_1+\frac{a_0}{b}=N' + \frac{a_0}{b}.$$

That is, the remainder $a_0$ of this division is the last digit in the desired representation. Dividing $N'$ by $b$, we obtain

$$\frac{N'}{b} = a_nb^{n-2}+a_{n-1}b^{n-3}+\cdots+a_2+\frac{a_1}{b},$$

and the remainder of this division is the next to the last digit in the desired representation. Proceeding in this way, we obtain all the digits $a_0,a_1,\ldots,a_n$. This procedure can be systematized quite conveniently, as shown below. Suppose, for example, we wish to express 198 to the base 4. We find

The desired representation is $(3012)_4$. Again, suppose we wish to express 6647 to the base 12, where $t$ and $e$ are employed to represent ten and eleven, respectively. We find

The desired representation is $(3t1e)_{12}$.

One is apt to forget, when adding or multiplying numbers in our ordinary system, that the actual work is accomplished mentally and that the number symbols are used merely to retain a record of the mental results. Our success and efficiency in carrying out such arithmetic operations depend on how well we know the addition and multiplication tables, the learning of which absorbed so much of our time in the primary grades. With corresponding tables constructed for a given base $b$, we can similarly perform additions and multiplications within the new system, without spending any time reverting to the ordinary system.

Let us illustrate with base 4. We first construct the following addition and multiplication tables for base 4.

The addition of 2 and 3, therefore, by reference to the table, is 11, and the multiplication of 2 and 3 is 12. Using these tables, exactly as we are accustomed to using the corresponding tables for base 10, we can now perform additions and multiplications. As an example, for the multiplication of $(3012)_4$ by $(233)_4$ we have, omitting the subscript 4,

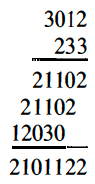
Considerable familiarity with the tables will be needed in order to perform the inverse operations of subtraction and division. This, of course, is also true for the base 10 and is the reason for much of the difficulty encountered in teaching the inverse operations in the elementary grades.

Radix fractions (description)

Before attempting problems in the next section concerning radix fractions, it may help to make some general number representation explorations first. We see in [12] that any whole number $N$ can be written uniquely in the form

$$N=a_nb^n + a_{n-1}b^{n-1}+\cdots+a_2b^2+a_1b+a_0,$$

where $0\leq a_i < b$. We can roughly and informally represent any number in base $b$ as follows:

$$N=\cdots+ab^3+cb^2+db^1+eb^0+fb^{-1}+gb^{-2}+\cdots$$

Such a number would notationally be represented as $N=\cdots acde.fg\cdots$ (base $b$). It is worth noting that the fraction may go on indefinitely (as is the case with $\frac{1}{3}=\overline{3}$), and the little dot . between $\cdots acde$ and $fg\cdots$ is referred to as the "radix point" or simply the "decimal point" when working with conventional base 10 numbers. Converting the number 12.112 (base 3) to base 10 is fairly simple if we just follow the informal representation given above:

$$(12.112)_3 =1(3^1)+2(3^0)+1(3^{-1})+1(3^{-2})+2(3^{-3})=3+2+\frac{1}{3}+\frac{1}{9}+\frac{2}{27}=\frac{149}{27}=5.518\overline{518}$$

More formally, suppose we want to represent a general number $N$ in base $b$ that accounts for both its whole number and fractional portions. We could write $N$ as

$$N=\sum_{i=\alpha}^{\beta} a_ib^i\qquad 0\leq a_i < b;\quad \alpha < 0 \leq\beta;\quad a,b,i,\alpha,\beta\in\Z$$

where the idea is that $\beta$ and $\alpha$ effectively serve as upper and lower bounds, respectively, with $\beta$ serving as the highest power of base $b$ needed to represent the number in question and the magnitude of $\alpha$ serving as how many digits to the right of the radix point we want to record (e.g., the hundredth place for a decimal fraction would be represented by $\alpha=-2\to |\alpha|=2$ places to the right of the decimal point). Hence, the whole number portion of $N$ could be represented by $\sum_{i=0}^\beta a_ib^i$ while its fractional portion could be represented by $\sum_{i=\alpha}^{-1}a_ib^i$.

All of this is a bit theoretical. What would this look like in practice? We can use our work above in converting $(12.112)_3$ to base 10 as an example. Since the highest power of 3 needed to represent this number is 1, we have $\beta=1$. Since we have 3 digits to the right of the radix point, we have $\alpha=-3$. Our generalized notation gives us the following:

$$\begin{align*} (12.112)_3 &= \sum_{i=-3}^1 a_ib^i & (\text{since $\alpha=-3$ and $\beta=1$})\\[1em] &= a_1b^1+a_0b^0+a_{-1}b^{-1}+a_{-2}b^{-2}+a_{-3}b^{-3} & (\text{by definition of $\Sigma$})\\[1em] &= 1(3^1) + 2(3^0) + 1(3^{-1}) + 1(3^{-2}) + 2(3^{-3}) & (\text{by previous work and since $b=3$})\\[1em] &= \frac{149}{27} & (\text{simplify})\\[1em] &= 5.518\overline{518} & (\text{simplify}) \end{align*}$$

Converting a number from base 10 to another base is somewhat trickier. The method for converting a base 10 number to another base is conveniently described in the previous section, but this method only works for those numbers to the left of the decimal point (whole numbers). We need to deal with the numbers to the right of the decimal point (the "fraction part"). To do this, we use a different and sort of backward version of the original method described in the previous section. The original method starts by dividing the number $N$ by the base $b$, and we then use the remainders to form the desired number in base $b$. We arrange the new number $N$ by putting together the remainders from bottom to top. This works for whole numbers.

To convert the fractional part of a number to another base, we must essentially use the method above in "reverse." We take the fractional part of the number (the portion to the right of the decimal or radix point) and multiply it by $b$. The integer parts that result from these multiplications play the same role that the remainders played when dividing by base $b$ in order to convert a whole number to a different base. We proceed to multiply whatever fractional part is left and we produce the number $N$ in the specified base $b$ in this way.

For example, to convert the number 14.73 to base 3, we must do the following: we first start out with the portion of the number to the left of the radix point (the whole number portion):

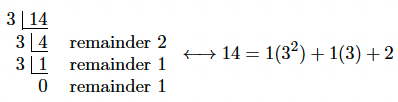
Assembling the remainders from bottom to top, we get 112 in base 3. That takes care of the whole number portion of 14.73. We must now convert .73 to base 3 to finish the complete conversion. As described above, the fractional conversion is basically the reverse of the previous method in the sense that now we will be multiplying by base $b$, keeping the resultant integer parts, and then assembling these parts from top to bottom instead of bottom to top:

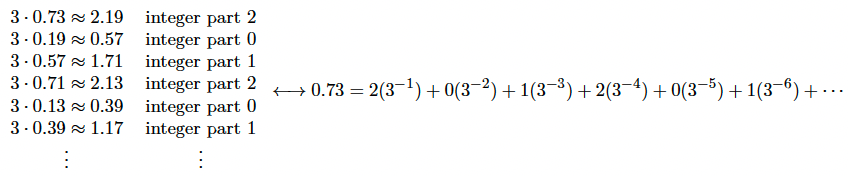
As seen above, we arrange the integer parts from top to bottom to get the fractional portion in base 3. Thus, we have the following (note that we could write down more fractional digits had we continued the process above):

$$14.73 = (14.73)_{10} = (112.201201)_3$$

In a nutshell, the method used above is the one you will want to use for converting the fractional part for a number in base 10 into base $b$. The following section provides a more formalized description of this process.

Expressing a number N in base b

If we have a number $N$ that is expressed using base 10, then we may express it using base $b$ if we can determine the integer values of

$$a_n,a_{n-1},a_{n-2},\ldots,a_2,a_1,a_0,a_{-1},a_{-2},\ldots,a_{-(m-1)},a_{-m}$$

in the expression

N=\underbrace{a_nb^n+a_{n-1}b^{n-1}+a_{n-2}b^{n-2}+\cdots+a_2b^2+a_1b^1+a_0b^0}_{\text{integer portion}}+\underbrace{a_{-1}b^{-1}+\cdots+a_{-(m-1)}b^{-(m-1)}+a_{-m}b^{-m}+\cdots}_{\text{fractional portion}},}

where $0\leq a_i < b$ and the integer or whole number portion of $N$, as noted in braces above, is given by

$$a_nb^n+a_{n-1}b^{n-1}+a_{n-2}b^{n-2}+\cdots+a_2b^2+a_1b^1+a_0b^0,$$

while the fractional portion of $N$ is given by

$$a_{-1}b^{-1}+\cdots+a_{-(m-1)}b^{-(m-1)}+a_{-m}b^{-m}+\cdots.$$

One will usually specify how many digits $m$ after the radix point are desired, thus eliminating the need for the trailing $+\cdots$ in the representation of the fractional portion of $N$.

To effectively express $N$ using base $b$, we need to employ a method that first converts the whole number portion of $N$ into base $b$ and then subsequently converts the fractional portion of $N$ into base $b$. We may then link together the results of these conversions to express the entire number $N$ in base $b$. To start, let us write $N = R + Q$, where $R$ represents the whole number portion of $N$, and $Q$ represents the fractional portion of $N$.

Converting the whole number portion of N into base b

First write out the expression for the whole number portion of $N$ (we omit $b^0$ for the sake of clarity since $b^0=1$, and we also express $b^1$ as simply $b$):

$$R=a_nb^n+a_{n-1}b^{n-1}+a_{n-2}b^{n-2}+\cdots+a_2b^2+a_1b+a_0\qquad (0\leq a_i < b)$$

Dividing the equation above by $b$ gives us the following:

$$\frac{R}{b}=a_nb^{n-1}+a_{n-1}b^{n-2}+\cdots+a_2b+a_1+\frac{a_0}{b}=R'+\frac{a_0}{b}$$

That is, the remainder $a_0$ of this division is the last digit in the desired representation.

How the remainder part works

Recall the division algorithm stated at the beginning of this section. We let $a$ represent the dividend (the number to be divided), $d$ the divisor (the number doing the dividing), and the claim was that unqiue integers $q$ and $r$ existed such that $a=dq+r$, where $0\leq r < d$. We call $q$ the quotient and $r$ the remainder.

In our case, $R$ is the dividend (the whole number portion of $N$ to be divided), and $b$ is the divisor (the number doing the dividing). The following way of rewriting $R$ may more clearly illustrate why $a_0$ is the remainder when dividing by $b$:

$$\begin{align*} \overbrace{R}^{\text{dividend}} &= a_nb^n+a_{n-1}b^{n-1}+a_{n-2}b^{n-2}+\cdots+a_2b^2+a_1b+a_0 & (\text{by definition})\\[1em] &= b(a_nb^{n-1}+a_{n-1}b^{n-2}+\cdots+a_2b+a_1) + a_0 & (\text{factor out $b$ strategically}) \\[1em] &= \underbrace{b}_{\text{divisor}}\cdot\underbrace{R'}_{\text{quotient}} + \underbrace{a_0}_{\text{remainder}} & (\text{by definition of $R'$}) \end{align*}$$

If we use $R'$ as the new dividend (and keep $b$ as the divisor), then we get the following:

$$\begin{align*} \overbrace{R'}^{\text{dividend}} &= a_nb^{n-1}+a_{n-1}b^{n-2}+\cdots+a_2b+a_1 & (\text{by previous work})\\[1em] &= b(a_nb^{n-2}+a_{n-1}b^{n-3}+\cdots+a_2) + a_1 & (\text{factor out $b$ strategically}) \\[1em] &= \underbrace{b}_{\text{divisor}}\cdot\underbrace{R''}_{\text{quotient}} + \underbrace{a_1}_{\text{remainder}} & (\text{by definition of $R''$}) \end{align*}$$

We continue this process until we obtain a quotient that is less than our base; that is, using the language of the division algorithm, we continue this process until we obtain a dividend that is less than its divisor. At that point, the "final quotient" is simply 0 and the remainder is the last quotient we obtained that is less than our base.

This procedural flow is pictured in the figure where the integer part of 14.73 is being converted to base 3:

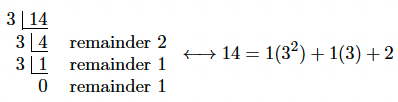
The upshot of all of this is that we can proceed in the way outlined above to obtain all the digits $a_0, a_1, \ldots, a_n$. The figure above simply provides a convenient systematization of the procedure.

We obtain all the digits $a_0, a_1, \ldots, a_n$ by proceeding in this manner (elaborated on in the note above).

Converting the fractional portion of N into base b

First write out the expression for the fractional portion of $N$:

$$Q=a_{-1}b^{-1}+a_{-2}b^{-2}+\cdots+a_{-(m-1)}b^{-(m-1)}+a_{-m}b^{-m}+\cdots\qquad (0\leq a_i < b)$$

If we multiply the equation above by $b$, then we get the following:

$$\begin{align*} Q\cdot b &= b(a_{-1}b^{-1}+a_{-2}b^{-2}+\cdots+a_{-(m-1)}b^{-(m-1)}+a_{-m}b^{-m}+\cdots) & (\text{by definition of $Q$})\\[1em] &= a_{-1}b^0 + a_{-2}b^{-1} + \cdots + a_{-(m-1)}b^{-(m-1)+1}+a_{-m}b^{-m+1}+\cdots & (\text{multiply})\\[1em] &= a_{-1} + a_{-2}b^{-1} + \cdots + a_{-(m-1)}b^{-(m-1)+1}+a_{-m}b^{-m+1}+\cdots & (\text{since $b^0=1$})\\[1em] &= a_{-1} + (a_{-2}b^{-1} + \cdots + a_{-(m-1)}b^{-(m-1)+1}+a_{-m}b^{-m+1}+\cdots) & (\text{rewrite})\\[1em] &= \underbrace{a_{-1}}_{\text{integer}} + \underbrace{Q'}_{\text{fractional}} & (\text{by definition of $Q'$}) \end{align*}$$

Recall that $0\leq a_i < b$; that is, $a_i$ is an integer. The expression above, namely $Qb = a_{-1} + Q'$, shows that $a_{-1}$ and $Q'$ represent the resultant integer and fractional portions of the multiplication of $Q$ by $b$, respectively. Of course, we can continue the process outlined above to obtain more fractional digits:

$$\begin{align*} Q'\cdot b &= b(a_{-2}b^{-1} + a_{-3}b^{-2} + \cdots + a_{-(m-1)}b^{-(m-1)+1}+a_{-m}b^{-m+1}+\cdots) & (\text{by definition of $Q'$})\\[1em] &= a_{-2}b^{0} + a_{-3}b^{-1} \cdots + a_{-(m-1)}b^{-(m-1)+2}+a_{-m}b^{-m+2}+\cdots & (\text{multiply})\\[1em] &= a_{-2} + a_{-3}b^{-1} \cdots + a_{-(m-1)}b^{-(m-1)+2}+a_{-m}b^{-m+2}+\cdots & (\text{since $b^0=1$})\\[1em] &= a_{-2} + (a_{-3}b^{-1} \cdots + a_{-(m-1)}b^{-(m-1)+2}+a_{-m}b^{-m+2}+\cdots) & (\text{rewrite})\\[1em] &= \underbrace{a_{-2}}_{\text{integer}} + \underbrace{Q''}_{\text{fractional}} & (\text{by definition of $Q''$}) \end{align*}$$

Proceeding in this way, we obtain the digits $a_{-1}, a_{-2}, \ldots, a_{-m}$, but we could go on obtaining digits indefinitely, as the process above indicates. Consider again the following picture (shown previously), which shows how to convert the fractional portion of 14.73 to base 3:

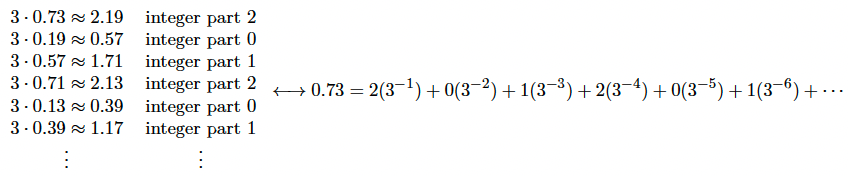
The reason why the procedure above works should now make much more sense logically.

Radix fractions (problems)

info

The following problems are taken from [12].

Fractional numbers can be expressed, in the ordinary scale, by digits following a decimal point. The same notation is also used for other bases; therefore, just as the expression .3012 stands for

$$3/10 + 0/10^2 + 1/10^3 + 2/10^4,$$

the expression $(.3012)_b$ stands for

$$3/b + 0/b^2 + 1/b^3 + 2/b^4.$$

An expression like $(.3012)_b$ is called a radix fraction for base $b$. A radix fraction for base 10 is commonly called a decimal fraction.

Radix fraction to decimal fraction

Problem: Show how to convert a radix fraction for base $b$ into a decimal fraction.

Solution: Consider the following number $N$ in base $b$:

N=\underbrace{a_nb^n+a_{n-1}b^{n-1}+a_{n-2}b^{n-2}+\cdots+a_2b^2+a_1b^1+a_0b^0}_{\text{integer portion}}+\underbrace{a_{-1}b^{-1}+\cdots+a_{-(m-1)}b^{-(m-1)}+a_{-m}b^{-m}+\cdots}_{\text{fractional portion}}.}

To convert a radix fraction for base $b$ into a decimal fraction, we simply use the expression for the fractional portion above and substitue in the $b$-value for whatever base $b$ we are using. Thus, to express $(0.112)_3$ as a decimal fraction, we simply write

$$1(3^{-1})+1(3^{-2})+2(3^{-3})=\frac{14}{27}=0.518518518\ldots$$

Decimal fraction to radix fraction

Problem: Show how to convert a decimal fraction into a radix fraction for base $b$.

Solution: To convert a decimal fraction into a radix fraction for base $b$, we use the method outlined in the section above (i.e., the section about converting the fractional portion of a number $N$ into base $b$).

Approximate radix fractions as decimal fractions

Problem: Approximate to four places $(.3012)_4$ and $(.3t1e)_{12}$ as decimal fractions.

Solution: Consider the following:

• $(0.3012)_4$: We may approximate out to four decimal places as follows:

  $$(0.3012)_4=3(4^{-1})+0(4^{-2})+1(4^{-3})+2(4^{-4})=\frac{99}{128}=0.7734375\ldots\approx 0.7734.$$

• $(3t1e)_{12}$: We may approximate out to four decimal places as follows:

  $$(3t1e)_{12}=3(12^{-1})+t(12^{-2})+1(12^{-3})+e(12^{-4})=\frac{433}{1728}+\frac{e}{20736}+\frac{t}{144}=0.32055\ldots\approx0.3206,$$

  when we substitute the values $t=10$ and $e=11$ into the fractions above.

Approximate a radix fraction in other bases

Problem: Approximate to four places .4402 as a radix fraction, first for base 7, and then for base 12.

Solution: Consider the following:

• 0.4402 as a radix fraction for base 7:

  

  Since we are only instructed to approximate out to four places, the above is satisfactory; of course, we could continue the process and obtain an even better approximation if we wanted.

• 0.4402 as a radix fraction for base 12: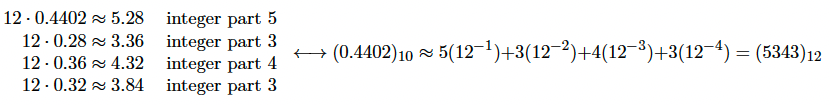

  

  As above, we may stop once we have approximated out to four places, thus concluding the problem.

---